[Настройки текста] [Cбросить фильтры]
[Оглавление]
Carlos М. Madrid Casado Наука. Величайшие теории: выпуск 34: Вначале была аксиома. Гильберт. Основания математики.
Еженедельное издание ISSN 2409-0069 Пер. с исп. — М.: Де Агостини, 2015. — 176 с. ISSN 2409-0069 © Carlos М. Madrid Casado, 2013 (текст) © RBA Collecionables S.A., 2013 © ООО «Де Агостини», 2014-2015Введение
Зайдите в любую библиотеку и окиньте взглядом ее стеллажи. Вы сразу обнаружите книги Евклида, Ньютона или Эйнштейна, а рядом — труды Платона, Аристотеля или Канта, не говоря о произведениях Сервантеса и Шекспира. Настоящее рядом с прекрасным. Но почему порядок именно такой? Возможно, все дело в небрежности библиотекаря или же, если не брать в расчет случайность, здесь есть какая-то глубинная причина? Вероятно, следует начать с вопроса: почему работы Евклида (а значит и Архимеда, Лейбница, Эйлера или Гаусса) все еще присутствуют в нашей жизни, почему они все еще актуальны? Ведь не зря труд Евклида «Начала геометрии» веками оставался учебником, который знакомил с научными истинами целые поколения студентов. Какой была роль геометрии и математики в целом во множестве знаний? Для одних математика стала дверью и ключом к науке, для других — еще и алфавитом философии. Однако на вопрос об основании и природе математики дали слишком много ответов. Почти столько же, сколько в мире было математиков, начиная с работавших под сенью пирамид землемеров, заканчивая нашими современниками и не забывая о греческих геометрах. С глубокой древности говоря «математика», подразумевают «доказательство». Доказательство, как клей, скрепляет математику. Но что такое доказательство? Ответу на этот вопрос наш герой, Давид Гильберт (1862-1943), посвятил значительную часть своей научной деятельности. В чем состоит доказательство математической теоремы? И все ли математические истины доказуемы? Эти и другие загадки, возникшие на стыке науки и философии, сосредоточились возле оснований математики. Глубокая озабоченность данным вопросом определяла привязанность Гильберта к этой науке. Давид Гильберт — пожалуй, один из значительнейших математиков XX века. Его работы в области алгебры, геометрии, анализа, физики, логики и оснований математики дают ему право называться математиком века. И это не пустые слова. Его вклад (как в качественном, так и в количественном отношении) обладает неизмеримой, беспрецедентной значимостью. Гильберт — ученый уровня Гаусса и Пуанкаре. Но в чем заключается легендарность этой личности? К постоянным нововведениям и выдающимся результатам, к которым привыкли его современники, следует добавить личную харизму, очаровывавшую тех, кто с ним встречался. Путь, проделанный математикой в XX веке, невозможно объяснить без учета его вклада. Его влияние сказалось на целом ряде поколений, работавших над теми знаменитыми проблемами, которые он обозначил в программе столетия. Он был математиком из математиков. В то время как личная жизнь ученого протекала в похвальном спокойствии, жизнь интеллектуальная бурлила приключениями. Такое положение дел, возможно, не вписывается в представления о герое, зато подходит образу творческой личности, и эта история только и ждет, чтобы ее рассказали. Гильберту посчастливилось жить в эпоху, когда и математика, и физика чрезвычайно прогрессировали, хотя параллельно испытывали глубокие потрясения, приведшие к новому математическому методу и к свершению революции в физике. Описываемый период пришелся на настоящий творческий расцвет, и Гильберт был среди ведущих действующих лиц. Обзор жизни и научной деятельности Давида Гильберта сосредоточится на нескольких этапах, обусловленных его математическими интересами (алгеброй, геометрией, анализом, теоретической физикой и основаниями математики): разрабатываемые им годами, они и определили его легендарную репутацию. Но в этой книге мы не только расскажем о понятиях, которые он ввел или в становление которых внес вклад; мы также познакомимся с некоторыми важнейшими деятелями науки начала XX века. Минковский, Пуанкаре, Эйнштейн, фон Нейман и Гедель появятся на этих страницах в числе многих других. Читатель получит удовольствие от знакомства и постоянных встреч с людьми, имена которых известны каждому студенту благодаря понятиям и теоремам, названным в их честь. Детство и молодость Гильберт провел в родном Кёнигсберге, а в зрелом возрасте переехал в Геттинген, где жил до конца своих дней. Будучи профессором университета, он способствовал созданию математического института, который привлек лучшие умы того времени. Вокруг него выстраивался авангард немецкой науки, да и европейской тоже, пока нацисты не превратили Геттинген в пустошь. Карьера молодого Гильберта пошла в гору, когда, к удивлению коллег, он решил насущную алгебраическую проблему, казавшуюся непреодолимой. Однако через некоторое время он оставил алгебру и переключился на основания геометрии, взяв на вооружение аксиоматический метод. В его работе этот метод имел решающее значение. Гильберт больше, чем кто-либо, научил математиков мыслить аксиоматически и определил новый метод как самый надежный в математической вселенной. На лекции, прочитанной им на Международном конгрессе математиков в Париже 8 августа 1900 года (в тот день стояла удушающая жара), он продемонстрировал научному сообществу свою проницательность, и его стали воспринимать как человека, за которым — будущее математики. Логика необходима этой науке, но именно проблемы обеспечивают ее жизнедеятельность. Круг из 23 проблем, сформулированных Гильбертом, определил равное количество вызовов, которые мотивировали ведущих математиков последующие 100 лет. В итоге математика стала развиваться во многих направлениях. Некоторые из этих проблем были решены однозначно (как, например, в случае континуум-гипотезы), в то время как другие (скажем, гипотеза Римана) все еще ждут своей очереди. Гильберт — легендарная личность и для физики тоже. Уравнения общей теории относительности — результат его творческой гениальности в не меньшей степени, чем гениальности Эйнштейна. Квантовая механика, в свою очередь, тесно связана с математической структурой, гильбертовым пространством. Кроме того, новый век стал свидетелем того, как немецкий математик очерчивает (не в полной мере осознавая это) новую область математического анализа — функциональный анализ. Однако самая обширная тема — это основания математики. Парадоксы логики и теории множеств, а также плеяда открытых вопросов о надежности классической математики спровоцировали глубокий раскол в научном сообществе и все нараставшие споры об основаниях этой дисциплины. К 1920 году, находясь на пике карьеры, наш герой ринулся создавать амбициозную программу основания, причем ему пришлось помериться силами с некоторыми виднейшими европейскими математиками. Как архитектор, исследующий фундамент старого дворца, который вот-вот рухнет, Гильберт пересмотрел основания математики, пытаясь устранить ее трещины и обеспечить ей устойчивость на долгие века. Он хотел стереть уродливое пятно парадоксов с идеального здания математики. На это его воодушевляла слепая вера в то, что можно доказать: математика, снабженная подходящими аксиомами, не содержит никаких противоречий, она устойчива. Это одна из главных проблем математики, которую Гильберт озвучил на лекции 1900 года. Изучая его вклад, мы вновь переживем это эпическое и страстное приключение в поисках точности, где сошлись великие логики и математики конца XIX — начала XX века: Фреге, Рассел, Кантор, Пуанкаре, Брауэр и Гёдель. Вдохновленные богатством современной им математики, эти ученые задумались о ее природе и целях. В ту пору выделились три тенденции. Логицизм, проявившийся у Фреге и оживленный Расселом, утверждал, что все математические принципы могут быть сведены к логическим законам. Интуиционизм — порождение Пуанкаре и Брауэра — отрицал методы классической математики, которые привели ее к парадоксам. И наконец, формализм, отождествляемый с мыслью Гильберта, стремился полностью аксиоматизировать математику, доказав, что аксиомы никогда не ведут к противоречию. Гильберт был лидером школы формализма, по сути он отстаивал позицию, что математические рассуждения могут быть представлены аксиоматически, в рамках формальной системы и без какого-либо упоминания о значении символов. Эта ключевая идея позволяла уклониться от любого упоминания о скользкой и парадоксальной бесконечности. Гильберт считал, что все математические теоремы можно вывести на основе одного или более правил посредством символического управления ограниченным числом аксиом, причем за конечное число шагов. Тогда можно было рассматривать математику как игру формул, а проблему доказательства непротиворечивости аксиом — как вопрос конечной сочетаемости, тщательного анализа формул, которые могут быть доказаны в рамках формальной системы, последовательностей символов, производимых системой. Но упорные попытки Гильберта решить этот вопрос, заложить основы математики, не вызывающие никакого рационального сомнения, закончились поражением. Об австрийском логике Курте Гёделе заговорили, когда в 1931 году он объявил: чтобы доказать непротиворечивость математики, методов Гильберта недостаточно. Теоремы Гёделя о неполноте стали ушатом холодной воды для самого Гильберта и его последователей. Более того, они означали крах его программы. Оказалось, что непротиворечивую устойчивость математики невозможно доказать. Непоколебимая убежденность в том, что математика — самая надежная из наук, вылилась для многих в историческое коллективное разочарование. Математика несет в себе черты неуверенности, случайности и необоснованности, но тем не менее продолжает прогрессировать. Гильберт олицетворял идеал математика межвоенного поколения. Его влияние прочитывается в современной математике — аксиоматической науке, изучающей абстрактные структуры. Она порвала с математикой прошлого, которая была сосредоточена на числах, формулах и фигурах, изначально ее составлявших. Давид Гильберт определенно являлся ученым-универсалом, поскольку знал почти все ответвления современной ему математики, и оказался последним представителем этого уже исчезнувшего вида.1862 Давид Гильберт появляется на свет в городе Кёнигсберге, Пруссия. 1880 Начинает изучать математику в Кёнигсбергском университете. Зарождается его дружба с Адольфом Гурвицем и в особенности с Германом Минковским. 1888 Его первая крупная математическая победа: он решает проблему Гордана в теории инвариантов. 1892 Становится ординарным профессором в Кёнигсбергском университете. Женится на Кёте Ерош. 1895 Благодаря стараниям Феликса Клейна становится профессором Гёттингенского университета. 1897 Публикует «Отчет о числах», сборник актуальных знаний в области алгебраической теории чисел. 1899 Публикует «Основания геометрии», в которых представляет все возможные геометрии посредством исключительно аксиоматического метода. 1900 Читает знаменитую лекцию «Проблемы математики» на II Международном конгрессе математиков в Париже. 1904 Возрождает принцип Дирихле для вариационного исчисления. 1912 Собирает в монографию все свои статьи об интегральных уравнениях, используемых физиками того времени, а также набор инструментов развития квантовой механики с 1925 года. 1915 Соревнуется с Альбертом Эйнштейном в выведении уравнений поля общей теории относительности. 1922 Практически в одиночку вновь пробуждает интерес к основаниям математики, стремясь доказать непротиворечивость классической математики, чтобы нейтрализовать скептицизм интуиционистов. 1928 В соавторстве с Вильгельмом Аккерманом публикует «Основы теоретической логики», первый учебник по математической логике в ее современном понимании. 1930 Уходит в отставку. Читает оптимистичную лекцию по случаю получения звания почетного гражданина Кёнигсберга, завершая ее лозунгом: «Мы должны знать. Мы будем знать». Курт Гёдель накладывает ограничения на формализм Гильберта на конгрессе, проходящем в то же время. 1934 В соавторстве с Паулем Бернайсом публикует первый том «Оснований математики», в который включены некоторые достижения в этой области. 1943 Умирает в Гёттингене (Германия) в то время, как своим жестоким чередом идет Вторая мировая война.
ГЛАВА 1 Основания геометрии
Карьера Гильберта пошла вверх, когда он решил хитрую проблему Гордана. Однако молодой ученый отложил алгебру и теорию чисел, чтобы полностью погрузиться в изучение оснований геометрии. Открытие неевклидовых геометрий стало шахом почти 2000-летней греческой геометрии. Переформулирование аксиоматического метода позволило Гильберту навести порядок в этой области и подчеркнуть, что нет единой справедливой геометрии: их много, и каждая обладает различным набором аксиом. Кёнигсберг, 1862 год. Прошло 58 лет после смерти Иммануила Канта и 120 с тех пор, как Леонард Эйлер (1707-1783) решил знаменитую проблему семи мостов. Давид Гильберт появился на свет 23 января в протестантской семье из среднего класса, которая вот уже два поколения жила в столице Восточной Пруссии. Пруссия в то время возглавила объединение Германии под руководством кайзера Вильгельма I и железного канцлера Отто фон Бисмарка. Отец будущего ученого был городским судьей и прививал сыну типичные прусские ценности: пунктуальность, дисциплину и чувство долга. Мать, наоборот, увлекалась философией, астрономией и, как рассказывают, простыми числами. В школьные годы Гильберт показал себя упорной, энергичной и решительной личностью, хотя в средней школе страдал от того, что учебный процесс выстраивался на заучивании. Он увлекался искусством, литературой и математикой, однако не считался вундеркиндом. В 1880 году он выдержал экзамен и был зачислен в университет, избрав математику, хотя родители хотели, чтобы он изучал право. Кёнигсберг — конечно, не Берлин, где развернули свою деятельность преподаватели уровня Карла Вейерштрасса (1815- 1897) и Леопольда Кронекера (1823-1891), но и здесь имелась прочная математическая традиция. Здесь когда-то работал Карл Якоби (1804-1851), считавшийся вторым после Гаусса немецким математиком. Так в каком же научном контексте получал образование Гильберт? В последней четверти XIX века предполагалось, что как дисциплина математика имеет три ответвления: анализ, алгебру и геометрию. Анализ — это исследование все более строгого использования бесконечно малых, решение дифференциальных уравнений и теория функций в целом. Алгебра постепенно перестала походить на предмет, который мы изучали в школе, и занималась уже абстрактными объектами, хотя и не исключала теорию чисел. Геометрия же включала в себя целое семейство плохо согласованных между собой составляющих: евклидову геометрию и неевклидовы геометрии (в том числе проективную), а также дифференциальную и алгебраическую геометрии, в которых использовались инструменты анализа и алгебры.Любая дисциплина проходит три фазы развития: наивную, формальную и критическую. Давид Гильберт
Гильберт успешно изучал курсы алгебры, анализа и геометрии. В университете же он познакомился с Германом Минковским (1864-1909), который стал его лучшим другом. Будучи однокурсником Гильберта, он был на два года младше него, он опережал курс на целый триместр. Когда ему только исполнилось 19, он получил гран-при в области математики, которую вручала Парижская академия наук (хотя все прошло не слишком гладко, поскольку заходила речь о плагиате). Друзья обычно прогуливались вместе и восхищенно обсуждали математику. В ходе этих прогулок они исследовали каждый уголок математического знания. Эту традицию студенческих лет они сохранили на всю жизнь. Получив степень доктора, Гильберт задумался о том, чтобы устроиться на должность приват-доцента, которая позволила бы ему преподавать в университете (пусть даже жалованье не было фиксированным и складывалось в зависимости от количества студентов). Для этого требовалось внести какой-нибудь оригинальный вклад в науку. С этой целью Гильберт отправился на встречу с Феликсом Клейном (1849-1925), одним из знаменитых математиков того времени. Годы спустя Клейн говорил, что сразу же понял: за этим юношей — будущее математики. По его совету Гильберт поехал в Париж, где познакомился с Анри Пуанкаре (1854-1912). Француз был на восемь лет старше Гильберта, но уже состоялся как ученый. Он считался главным представителем французской математики, которая надеялась обойти немцев. В результате Пуанкаре и Гильберт не нашли общий язык, со временем они даже стали открыто соперничать. Тут крылась конкуренция за главенствование в математике будущего (отношения Пуанкаре и Клейна также не были хорошими: у последнего это противостояние даже вылилось в депрессию). На обратном пути Гильберт задержался в Гёттингенском университете и навестил недавно обосновавшегося там Клейна. Тот познакомил его с Паулем Горданом (1837-1912), одним из главных экспертов по теории инвариантов — области, в которой Гильберт добился своего первого большого успеха.
ОТ АЛГЕБРЫ К ТЕОРИИ ЧИСЕЛ
Теория инвариантов представляла собой ответвление алгебры XIX века и рассматривала, какие величины не изменяются (остаются инвариантными), когда мы преобразуем один многочлен в другой в соответствии с определенными правилами. Одна из самых любопытных проблем получила название проблемы Гордана. В 1868 году Гильберт ошарашил современников, предложив революционное решение задачи, которое король теории инвариантов Гордан назвал «теологическим». Гильберту удалось сделать то, к чему уже несколько лет стремились все эксперты по инвариантам: доказать так называемую основную теорему теории инвариантов, в которой утверждается, что любая система инвариантов образована конечным образом (проще говоря, что любой инвариант системы может быть представлен в виде сочетания небольшого количества инвариантов, образующих базис). Эту задачу не назовешь пустяковой. Однако нас интересует не ее содержание, а форма ее доказательства Гильбертом, поскольку это поможет представить путь развития его исследовательской карьеры. Как и в других областях математики, Гильберт разработал множество элементов, составивших новый подход. В данном случае он структурный алгебраический, сосредоточенный на структурах математических объектов в большей степени, чем на собственно математических объектах, а на группах, идеалах, кольцах и телах (алгебраических структурах) — в большей степени, чем на самих числах или конкретных многочленах, которые они содержат. Не осознавая этого, Гильберт готовил абстрактную алгебру XX века и мимоходом утвердил новый математический метод, знаменосцем которого стал позже. Подход Гильберта разительно отличался от традиционного. Вместо того чтобы открыто искать решение проблемы, он доказал: проблема не может не иметь решения. Его доказательство было не конструктивным, а экзистенциальным. Он не предлагал решения напрямую («вот базис инвариантов»), а только доказывал, что оно обязательно должно быть («если бы не было базиса инвариантов, мы бы пришли к противоречию»). Следовательно, доказательство основной теоремы осуществлялось путем доведения до абсурда. Эта аргументация не была единодушно принята математическим сообществом. Кронекер — одна из главных фигур немецкой математики того времени — высказался в этом отношении довольно резко. По слухам, подход Гильберта многим показался «зловещим». Для Кронекера доказательство существования обязательно означало построение того объекта, существование которого требовалось доказать. В данном случае это построение базиса инвариантов, которое, по утверждению Гильберта, существует. Он не принимал аргументов, что отсутствие существования базиса предполагает противоречие, следовательно, данный базис обязательно должен существовать, хотя его вычисление неосуществимо.КОНСТРУКТИВНЫЕ И ЭКЗИСТЕНЦИАЛЬНЫЕ ДОКАЗАТЕЛЬСТВА
Чтобы понять разницу, рассмотрим пример. Если вопрос заключается в том, имеет ли уравнение х2 - 1 = 0 решение, у нас есть два варианта. Первый — найти решение с помощью вычислений и алгебраических манипуляций: х = 1 и х = -1. Второй — попытаться ответить косвенно: задействовав некую теорему, показать, что уравнение имеет решение, хотя мы не можем его найти. Естественно, второй путь оказывается эффективнее, когда математик сталкивается с намного более сложными проблемами, чем решение простого уравнения второй степени. Очень часто в уравнениях высшей степени легче доказать существование решения, чем найти его.Путь, известный со времен Античности
Эта характеристика является общей для многих математических проблем. Евклид доказал, что существует бесконечное количество простых чисел без необходимости перечислять их все. Он выстраивал свое рассуждение путем доведения до абсурда. Первый шаг в таком доказательстве состоит в том, чтобы отрицать высказывание, которое нужно доказать. Чтобы доказать, что существует бесконечное количество простых чисел, Евклид предположил, что их число конечное: р1 р2,... Рn. На основе этого предположения он делал выводы, пока не пришел к абсурдному утверждению. Если предположить, будто есть только n простых чисел, то либо число р1 х р2 х ... х рn + 1 (образованное произведением их всех плюс один) является простым, либо не является. В первом случае отмечается противоречие, поскольку это новое простое число не является ни одним из партии. Во втором случае, если это не простое число, оно должно делиться на простое число, но ни одно из чисел р1, р2,... рn явно не является его делителем (деление неточное, оно дает 1 в остатке). И тут мы вновь сталкиваемся с противоречием. Следовательно, гипотеза, что существует конечное количество простых чисел, ложная: их должно быть бесконечное количество (хотя мы не можем определить их по одному). Доведение до абсурда, которое так любили Евклид и Гильберт, — один из лучших математических инструментов.Гильберт опубликовал статью в 1890 году в журнале Mathematische Annalen, который издавал Клейн. Рецензентом выступил сам Гордан, и хотя вначале он потребовал внесения существенных изменений, в итоге признал революционный подход Гильберта. Работы Гордана составляли ужасно длинные и сложные вычисления, они контрастировали с краткой, элегантной и лаконичной статьей Гильберта, в основе которой лежало доведение до абсурда. Однако потребовалось решительное вмешательство Клейна, чтобы примирить их, поскольку Гильберт не желал трогать ни единой запятой в своей статье. В конце концов Гордан признал, что даже у теологии есть свое применение. Гильберт бросил вызов и выиграл у тех, кто настаивал, будто математические доказательства должны базироваться на методе, рассматривающем сущности, наличие которых нужно доказать. Он доказал, что предположение о ложности гипотезы Гордана («существует базис инвариантов») ведет к противоречию. Этого было достаточно. Много лет спустя Гильберт объяснял своим студентам разницу между конструктивными доказательствами и теми, которые таковыми не являются (экзистенциальными), подчеркивая, что в аудитории есть кто-то, у кого на голове волос меньше, чем у других (никто из присутствующих не был абсолютно лысым), хотя мы не располагаем никаким способом выявить этого человека.
Это не математика! Это теология! Гордан после ознакомления с доказательством Гильберта
На кон было поставлено не только будущее теории инвариантов (область исследования, которую Гильберт практически закрыл), но и нечто большее — противостояние двух подходов к математике: конструктивного — характерного для XIX века — и экзистенциального, свойственного XX столетию (когда слово «существовать» имело лишь одно значение: быть лишенным противоречия). Экзистенциальный подход Гильберта в дальнейшем обеспечил ему многие победы и многие споры. Наконец, в 1892 году усилия Гильберта увенчались успехом, и он получил должность ординарного профессора Кёнигсбергского университета. Несмотря на то что в итоге он стал блестящим преподавателем, в начале его лекции едва привлекали студентов.
СОВРЕМЕННАЯ АЛГЕБРА И NULLSTELLENSATZ
Вавилоняне, египтяне и греки решали уравнения первой и второй степени, используя различные алгебраические техники. Следы греческой геометрической алгебры заметны по выражениям вроде «квадрат» и «куб» для второй и третьей степеней: «а в квадрате» — это квадрат со стороной а, а «а в кубе» — это куб с ребром а. Введение нового символьного аппарата (Диофант, Аль-Хорезми, Виет) определило настоящий прорыв в развитии алгебры и ее последующее отделение. В эпоху Возрождения Тарталья (по- итальянски «заика») вывел формулу для решения уравнений третьей степени, но предпочел держать ее в секрете. Астролог и математик Джероламо Кардано убедил его открыть ее и затем опубликовал, выдавав за свою. Лодовико Феррари, бывший секретарь Кардано, получил другую формулу для решения уравнений четвертой степени, однако решение в радикалах полиномиального уравнения пятой степени им не далось. Через 300 лет Абель доказал, что это невозможно. Гаусс в возрасте 52 лет. Литография из журнала «Астрономические новости», 1828 год.
Гаусс в возрасте 52 лет. Литография из журнала «Астрономические новости», 1828 год.
Гаусс и основная теорема алгебры
Чтобы больше узнать о рождении современной алгебры, следует обратиться к докторской диссертации Гаусса, которую тот защитил в 1797 году. Гениальный Гаусс доказал то, что сегодня известно как основная теорема алгебры: любое полиномиальное уравнение степени п имеет ровно п решений среди комплексных чисел. Хотя этот результат допускал Декарт (различая действительные и мнимые корни), а также со множеством ошибок доказал Д’Аламбер, только доказательство Гаусса было исчерпывающим. Его работа радикально изменила облик алгебры. Именно этот долгий путь Гильберта сквозь теорию инвариантов определил Nullstellensatz, или теорему о нулях, — мощный результат, обобщивший основную теорему алгебры для того случая, когда вместо уравнения имеется система алгебраических уравнений.Гильберт не впадал в отчаяние и расценивал этот период как процесс медленного, но стабильного созревания. Тогда же он женился на Кёте Ерош (его любимой партнерше по танцам), с которой был знаком с детства. Через год родился их единственный сын Франц, у которого еще в детстве проявилось серьезное умственное заболевание. Когда у юноши диагностировали шизофрению, отец поместил его в лечебницу для душевнобольных, где тот провел значительную часть своей жизни. С тех пор Гильберт держался так, будто у него никогда не было сына. В 1895 году он кардинально изменил свою жизнь. В конфиденциальном письме его уведомили о назначении — по рекомендации Клейна — профессором престижного Гёттингенского университета, где до того работали два таких колосса математики, как Гаусс и Риман. Его не пришлось упрашивать, он переехал и никогда не покидал Гёттинген. Между тем с теории инвариантов Гильберт уже переключился на теорию чисел — типично немецкую дисциплину с тех пор, как Гаусс опубликовал «Арифметические исследования» (1801) и назвал ее царицей математики. Немецкое математическое общество (основанное в 1890 году под председательством Георга Кантора (1845-1918)) поручило Гильберту и Минковскому разработать отчет о состоянии вопроса. Минковский сразу отказался, сославшись на занятость, зато Гильберт сделал намного больше, чем от него ожидали. Результатом была жемчужина математической литературы, ставшая в дальнейшем классикой в этой области знания, — Der Zahlbericht («Отчет о числах»), датированная 10 апреля 1897 года. В этой работе Гильберт объединил все имеющиеся данные, организовав их с новой точки зрения, переписал формулировки и доказательства. Он не только перераспределил детали головоломки, которую представляла собой алгебраическая теория чисел, но и заполнил лакуны оригинальными исследованиями. В предисловии к отчету он писал: «Теория чисел — это здание редкой красоты и гармонии. [...] Целью данного отчета является описание с единой точки зрения результатов теории чисел с ее доказательствами, с ее логическим развитием, что должно приблизить тот день, когда достижения классиков в области теории чисел станут общим достоянием всех математиков».
ПЕРВАЯ НАУЧНАЯ РЕВОЛЮЦИЯ
Древние вавилонская и египетская цивилизации имели значительные знания в области геометрии. Но их, если можно так выразиться, «математика» не вышла за пределы технической стадии, основываясь на сборниках инструкций для решения повседневных проблем, которые были связаны с трудом землемеров и в которых едва прослеживалось понятие доказательства. Геометрические теоремы Фалеса Милетского (ок. 624 — ок. 546 до н.э.) заставили бы улыбнуться египетских землемеров ввиду их простоты и бесполезности («Диаметр делит круг на две равные части»). Однако мы говорим о первых теоремах, которые являются истинными спустя более чем 2000 лет. Фалесу удалось измерить высоту пирамиды Хеопса с использованием простого правила пропорциональности. Пифагору также удалось установить логическую связь с наследием вавилонян и египтян. Под руководством Платона Афинская академия систематизировала пифагорейскую математику, особенно заметен вклад Теэтета (ок. 417 — ок. 369 до н.э.) и Евдокса (ок. 390 — ок. 337 до н.э.). Первому приписывают теорему, гласящую, что существует только пять правильных многогранников, пять Платоновых тел. Тогда же геометров того времени завораживали три классические проблемы: трисекция угла, квадратура круга и удвоение куба. Перейдя из Афинской академии в Александрийский мусейон, мы встретились бы с Евклидом, работа которого (наряду с работой Аполлония и Архимеда) завершает золотую эпоху греческой геометрии. Идеализированный портрет Евклида. Юстус ван Гент, 1474 год.
Идеализированный портрет Евклида. Юстус ван Гент, 1474 год.
«Отчет о числах» перенес Гильберта в авангард европейской математики. Конечно, анализируя его раннюю математическую деятельность, можно подумать, будто это отличный исследователь, но в узкой сфере знаний. Почти невозможно было предвидеть дальнейшее восхождение Гильберта на вершину математического Олимпа и общую убежденность в том, что, как и Пуанкаре, он является одним из последних математиков-универсалов, ориентирующихся во всех областях науки, включая его следующее завоевание — геометрию. Но чтобы показать вклад Гильберта в этой области, нужно вспомнить об исторической подоплеке, о том толчке, который XIX век обеспечил геометрии, о том, как открытие неевклидовых геометрий изменило аксиоматический метод.
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
Греческая геометрия была краеугольным камнем математики в течение нескольких веков. В «Началах» — трактате, восходящем к 300 году до н.э., — Евклид предложил аксиоматическое, чрезвычайно упорядоченное и структурированное представление о корпусе знаний, переданных математиками школ Пифагора и Платона. Его изложение, на которое повлияли размышления Аристотеля о логике, обладало очень примечательной характеристикой — чрезвычайной строгостью при доказательстве каждой теоремы. «Начала» состоят из 13 книг и содержат 465 геометрических пропозиций, от базовых принципов до самых проработанных выводов. Евклид начинает Книгу I списком из 23 определений основных геометрических терминов (точка, прямая, треугольник, окружность и так далее). Например: «Точка есть то, что не имеет частей». Затем Евклид приводит пять постулатов, на которых базируется вся его геометрия. Эти постулаты представлены без доказательства и обоснования, их просто нужно принять как предпосылки к изложенному дальше. Например: «Между двумя любыми точками можно провести прямую линию». После определений и геометрических постулатов Евклид уточняет ряд общих понятий и неоспоримых истин. Например: «Целое больше части» или «Равные одному и тому же равны и между собой». С этого момента Евклид начинает углубляться в предмет. Так, в первой пропозиции «Начал» показано, как построить равносторонний треугольник на заданном линейном отрезке. В то время как общие понятия имеют чисто логическое происхождение, постулаты (или аксиомы) обладают геометрической природой. Они уточняют правила работы с математическими объектами, которые Евклид определил до этого. Эти пять постулатов, или аксиом, следующие. 1. От всякой точки до всякой точки можно провести прямую. 2. Ограниченную прямую можно непрерывно продолжать по прямой. 3. Из всякого центра всяким раствором может быть описан круг. 4. Все прямые углы равны между собой. Иллюстрация пятого постулата Евклида.
Иллюстрация пятого постулата Евклида.
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых (см. рисунок на предыдущей странице). В отличие от прочих, пятый постулат Евклида довольно неочевиден, и это привело к тому, что многие математики — например, Птолемей (II век), Джон Валлис (1616-1703) и Иероним Саккери (1667-1733) — безуспешно пытались доказать его через остальные постулаты. В попытках доказательства каждый из них превосходил другого по утонченности и находчивости. Но единственным, чего они добились, стали формулировки, равносильные пятому постулату. Одна из них — знаменитая аксиома параллельных прямых. «Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной» (см. рисунок выше). Другая версия провозглашает, что «Сумма углов треугольника равна 180°». Однако историю о пятом постулате, или аксиоме параллельных прямых, ждал удивительный финал.
 Иллюстрация аксиомы параллельных прямых.
Иллюстрация аксиомы параллельных прямых.
Как математикам удалось освободиться от цепей евклидовой геометрии? Более 2000 лет они были убеждены, что это единственно возможная геометрия, единственное убедительное описание мира, поскольку изучалось только одно физическое пространство. Но в XIX веке открытие различных геометрий (в которых не выполнялась аксиома параллельных прямых) усилило их тревогу и заставило признать ошибку. Этот животрепещущий вопрос касался формы мира (если он действительно имеет какую-то форму). Первой неевклидовой геометрией, с которой смирились математики, оказалась, как ни странно, старая знакомая — проективная геометрия. Она начала свой путь в эпоху Возрождения, когда художники заинтересовались проецированием пространства на холст. Тогда было открыто одно из отличительных свойств проективной геометрии (которое радикально отличает ее от неевклидовой): две прямые, которые в трехмерном пространстве представлены как параллельные, на двумерном холсте предстают как пара прямых, пересекающихся на линии горизонта, в бесконечности. Точно так же железнодорожные рельсы, параллельные по всей длине, на фотографиях кажутся пересекающимися в точке схода. Так что в проективной геометрии две любые точки всегда пересекаются: либо в конкретной точке, либо в бесконечности. Следовательно, проективная геометрия противоречит аксиоме параллельных прямых, поскольку через точку, не лежащую на данной прямой, не проходит ни одной прямой, параллельной первой. В начале XIX века в проективной геометрии наметился прорыв, и совершил его французский математик Виктор Понселе (1788-1867). Этот наполеоновский офицер, оказавшись в российском плену, посвятил себя усовершенствованию идей в данной области и по возвращении домой опубликовал «Трактат о проективных свойствах фигур» (1822). В нем Понселе ввел понятие проективной геометрии как сферы знания, рассматривающей свойства фигур, которые сохраняются при проецировании, то есть свойств, общих для фигур с их тенями и проекциями. Эти свойства включают в себя отношения принадлежности, но не отношения расстояния или размера. Так, если три точки лежат на одной прямой, при проецировании они на одной прямой и остаются, но очень вероятно, что расстояние между ними изменится. Точно так же тень, которую отбрасывает каждый из нас, не равна нам по размеру. Через некоторое время немецкий математик Юлиус Плюккер (1801-1868) включил в проективную геометрию координаты, что позволило ему алгебраизировать ее и доказать многочисленные результаты с аналитической точки зрения. В результате проективная геометрия составляла особый случай неевклидовой геометрии. Аксиома параллельных прямых не выполнялась (поскольку на проективной плоскости не существовало параллельных прямых), но проективная геометрия отрицала не только аксиому параллельных прямых, но и параметры углов и расстояние (поскольку при проецировании они не сохраняются). Не выполнялся не только пятый, но и четвертый постулаты Евклида (об углах). Поэтому математики не стали рассматривать проективную геометрию как настоящую неевклидову геометрию. Казавшаяся недостижимой цель заключалась в том, чтобы с нуля построить новую геометрию, которая выполняла бы евклидовы аксиомы, кроме аксиомы параллельных прямых. Поскольку она отрицалась, оставалось два пути: либо отрицать существование параллельных прямых («не существует параллельных прямых»), либо отрицать единственность прямой, параллельной данной, проходящей через точку, не лежащую на ней («существует более одной параллельной прямой»).
ПРОГРАММА ЭРЛАНГЕНА
Феликс Клейн (1849-1925), учитель Гильберта, проповедовал четкое видение геометрии. Любая геометрия состоит из пространства и группы трансформаций. Для Клейна геометрия заключалась в изучении свойств объектов, которые остаются инвариантными к некоторой группе трансформаций, или предварительно заданных движений. Уверовав в роль проективной геометрии, он доказал, что раз она задана группой проекций — наибольшей группой, — то представляет собой основную геометрию, базирующуюся на минимальном числе начальных гипотез. Все прочие геометрии проистекают из нее, порождая дополнительные гипотезы. Именно так произошло с евклидовой геометрией, которая наследовала все проективные свойства. Этот тезис он развивал в своей инаугурационной речи, когда в 1872 году заступал на должность главы кафедры Эрлангенского университета. Феликс Клейн.
Феликс Клейн.
Как Карл Фридрих Гаусс (1777-1855), так и Янош Бойяи (1802-1860) и Николай Лобачевский (1792-1856) приняли существование параллельных прямых и отрицали их единственность: через одну точку, не лежащую на прямой, проходит более одной параллельной прямой. Этим трем математикам удалось вывести достаточный ряд теорем воображаемой геометрии, не столкнувшись ни с абсурдом, ни с каким-либо парадоксом. Но не ожидали ли они их за углом? Разве можно быть уверенными в том, что пойди они дальше, их выводы не разбились бы о какое-нибудь противоречие? В середине века назрела необходимость в модели этой новой геометрии в рамках евклидова учения, чтобы даже в случае скрытого в ней противоречия она так же оставалась частью почитаемой евклидовой геометрии (что казалось невозможным). С этой позиции можно было раз и навсегда доказать, что справедливость новой геометрии заключается именно в справедливости евклидовой геометрии, которая считалась надежной. Поставленную задачу частично решил Эудженио Бельтрами (1835-1900), предложив в 1868 году локальную модель — псевдосферу. Через два года Клейн открыл первую полноценную модель неевклидовой геометрии.
Ради Бога, молю тебя, оставь эту материю, потому что она может лишить тебя всего твоего времени, здоровья, покоя, всего счастья твоей жизни. Письмо, отправленное Фаркашем Бойяи своему сыну Яношу после того, как он узнал, что тот работает над пятым постулатом Евклида
Рассмотрим модель Клейна. Допустим, что наше пространство свелось к внутренности круга (за исключением его краев), и создадим что-то вроде словаря, в котором будет установлено поочередное соответствие ряда терминов — как в обычном двуязычном словаре, в котором значение слов то же. Когда Евклид говорит: «точка», мы думаем о точках внутри этого круга, когда он говорит: «прямая», подразумеваются отрезки, которые начинаются и заканчиваются на краю круга. Такой перевод позволяет построить модель неевклидовой геометрии внутри собственно евклидова пространства. Что происходит с аксиомой параллельных прямых. При заданной прямой r и не лежащей на ней точке А существует более одной прямой, параллельной r, которая проходит через А. Действительно, прямые s и t параллельны прямой r внутри круга, поскольку они никогда не пересекаются в нашем пространстве (см. рисунок 1). Буквально из ничего была создана новая странная вселенная. Евклид был серьезным образом потеснен.
 РИС. 1
РИС. 1
Сомнения касательно неевклидовой геометрии не рассеялись, даже когда распространились идеи диссертации «О гипотезах, лежащих в основе геометрии», написанной Бернхардом Риманом (1826-1866). В 1854 году он прочитал ее 80-летнему Гауссу, который не скрыл своего энтузиазма в отношении услышанного, однако опубликована эта работа была лишь после его смерти. Основываясь на исследованиях Гаусса в области дифференциальной геометрии, Риман предположил, что в каждом пространстве может быть определена различная форма измерения расстояния, так что прямая в этом пространстве (которая по определению является «самым коротким путем между двумя точками») не совпадает с имеющимися у нас представлениями о ней. Итоговая особенная кривая, так называемая геодезическая, будет играть в этом пространстве роль, которую прямая линия играет в евклидовой геометрии. Согласно Риману, для евклидова пространства характерна постоянная нулевая кривизна, где есть единственная параллельная прямая (см. рисунок 2 [1]). Но если изменить значение кривизны, мы получим другой тип пространства, который окажется моделью неевклидовой геометрии. Если кривизна отрицательная, мы получим гиперболическую геометрию Гаусса — Бойяи — Лобачевского, где через точку, не лежащую на прямой, проходит более одной параллельной ей прямой [2]. И наоборот, если кривизна положительная, мы получим эллиптическую геометрию, в которой нет параллельных прямых [3].
 РИС. 2
РИС. 2
Риман помог истолковать сферу в качестве модели эллиптической геометрии, а следовательно — неевклидовой геометрии, в которой аксиома параллельных прямых ложная, в том смысле, что нет параллельных прямых (как, допустим, в проективной геометрии). В сфере роль прямых берут на себя наибольшие круги. То есть если мы назовем прямыми наибольшие круги, то получим евклидову модель эллиптической геометрии. Два любых наибольших круга всегда пересекаются. Это случай меридианов Земли, которые всегда пересекаются на полюсах. Поскольку аксиома параллельных прямых не выполняется, сумма углов треугольника не составляет 180°, что показано на сферическом треугольнике на рисунке 3, углы которого в сумме дают 230°. Однако локально, в небольшом масштабе, евклидова геометрия, похоже, выполняется (см. рисунок 4, сумма углов треугольника составляет 180°). Эти открытия позволили Риману рассматривать проективную плоскость в контексте сферической геометрии. Так что неевклидовы геометрические модели, извлеченные на свет математиками XIX века, только вернули данный вопрос в рамки евклидовой геометрии. Если последняя раньше считалась единственно справедливой, теперь же странные неевклидовы геометрии рассматривались наравне с евклидовой геометрией (которая оказывалась их особым случаем), и возникал правомерный вопрос: в чем же справедливость евклидовой геометрии? Можно ли с уверенностью утверждать, что она не содержит никаких противоречий? Важнейшим следствием из признания неевклидовых геометрий была необходимость рассмотреть проблему справедливости геометрии и всей математики с точки зрения оснований. До тех пор связность евклидовой геометрии обеспечивало то, что она соответствовала физическому пространству, в котором нет противоречий. Кроме интересных результатов, количество которых постоянно возрастало, внимание также привлекали и основополагающие вопросы. Аксиоматический подход последней трети XIX века, во главе которого стояли Мориц Паш (1843-1930) и Джузеппе Пеано (1858-1930), обозначил их особенно остро, и только Гильберт смог дать определенный ответ. Но прежде требовалось найти подходящую аксиоматику евклидовой геометрии, которая закрыла бы постепенно открывающиеся логические бреши.
АКСИОМАТИЧЕСКИЙ ПОДХОД ГИЛЬБЕРТА
Как это было с теорией инвариантов, настал день, когда Гильберт устал и оставил теорию чисел, переключившись на основы геометрии. Никто не ожидал такого, пусть даже он и вел два курса по этому предмету в Кёнигсберге. Эта новость застала врасплох всех его новых коллег по Гёттингену. Однако в своем «Отчете о числах» Гильберт подчеркивал, что современная математика развивается под знаком числа, и потому призывал к арифметизации геометрии, ориентированной на логический анализ последней. В этом угадываются зачатки его знаменитых Grundlagen der Geometrie («Основания геометрии»), публикация которых в 1899 году была приурочена к открытию в Гёттингене статуи Гаусса и Вебера в память об изобретении ими телеграфа. Эта работа сразу же обозначила новую парадигму исследования оснований и аксиоматическую практику в XX веке, как «Начала» за несколько веков до этого. В книге излагалась аксиоматика геометрии, которая на голову превосходила аксиоматику не только Евклида, но и предложенные Пашем и Пеано. Гильберт заявил, что работа по установлению минимального числа гипотез, из которых можно вывести всю геометрию, осуществлена не полностью, и сформулировал 21 аксиому. Эти аксиомы возникли не из ниоткуда, их скрыто или открыто применяли еще в древности. Они были продуктом не чистой мысли, а скорее интуиции (это логично, учитывая, что книгу открывает цитата из Канта). В том виде, как ее задумывал Гильберт, геометрия была ближе к механике и физике, чем к алгебре и теории чисел. Гильберт сформулировал свои аксиомы для трех систем неопределенных объектов. Объекты первой системы он назвал точками; второй — прямыми; а третьей — плоскостями. Но, в отличие от Евклида, он не дал определений элементарным геометрическим понятиям. Сами аксиомы определяют их, устанавливая внутренние отношения. В них самих содержатся утверждения о точках, прямых и плоскостях и о том, что с ними можно делать. По Гильберту, нужно избавиться от налета толкований элементарных объектов. Аксиомы, и только они (без каких-либо предварительных определений или рисунков), характеризуют элементарные объекты через их взаимоотношения. «Следует добиться того, чтобы с равным успехом можно было говорить вместо точек, прямых и плоскостей о столах, стульях и пивных кружках», — писал он. Аксиомы допускают множественные толкования, и в этом коренное различие материальной аксиоматики Евклида и новой формальной аксиоматики Гильберта. Используя все свое математическое умение, 21 аксиому евклидовой геометрии он классифицировал по пяти группам: — аксиомы принадлежности, которые связывают между собой различные объекты, например позволяют утверждать, что «эта точка принадлежит этой прямой» или «эта прямая принадлежит этой плоскости»; — аксиомы порядка, которые позволяют утверждать, что, например, «эта точка лежит между этими двумя» (как отметил Паш, данный тип аксиом полностью отсутствовал среди евклидовых постулатов); — аксиомы конгруэнтности, определяющие соразмерность отрезков; — аксиома параллельности имеет знаменитую формулировку о параллельных прямых; — аксиомы непрерывности, их две: так называемая аксиома Архимеда, которая гласит, что если последовательно повторять любой из двух заданных произвольных отрезках, мы можем построить отрезок большего размера, чем первый, за конечное число шагов; и аксиома полноты линии, или непрерывности прямой, она гласит, что точки одной прямой образуют систему, неподверженную какому- либо расширению при условии сохранения линейного порядка и отсутствии противоречия аксиоме конгруэнтности и аксиоме Архимеда. Без аксиомы непрерывности нельзя утверждать, что две окружности пересекутся в точке С и,следовательно, что можно построить равносторонний треугольник со стороной АВ (как это заявлено в Пропозиции I Книги I «Начал» Евклида).
Без аксиомы непрерывности нельзя утверждать, что две окружности пересекутся в точке С и,следовательно, что можно построить равносторонний треугольник со стороной АВ (как это заявлено в Пропозиции I Книги I «Начал» Евклида).
Последней аксиомы в «Началах» не было, хотя необходимость в ней возникает даже при доказательстве Пропозиции I Книги I. То, что Гильберт извлек ее на свет, составляет один из важнейших его вкладов. Без нее Q2 (то есть плоскость, в которой у точек есть только рациональные координаты) было бы моделью евклидовой геометрии, поскольку она бы удовлетворяла всем предыдущим аксиомам. Однако, как подчеркнул Рихард Дедекинд (1831-1916), в этой дырявой плоскости две окружности, каждая из которых проходит через центр другой, необязательно должны пересекаться (что предполагалось в Пропозиции I), потому что это возможно в точке с иррациональными координатами (в дырке). Аксиома полноты линии, или непрерывности прямой, позволяет определить любую прямую с действительными числами R и, следовательно, плоскость R2 (то есть полную плоскость со всеми точками с рациональными и иррациональными координатами), где две окружности гарантированно пересекутся (см. рисунок). Это мост между синтетической геометрией, основанной на диаграммах и чертежах, и аналитической, выстраиваемой на вычислениях.
АКСИОМЫ, ДОКАЗАТЕЛЬСТВА, ТЕОРЕМЫ И ТЕОРИИ
С аксиоматической точки зрения аксиома — это высказывание, по той или иной причине (обычно из-за ее плодотворности) помещенное в основание математической теории, чтобы из него в дальнейшем можно было вывести теоремы. Но чтобы вывести теоремы, необходим свод правил выведения. Математики обычно оперируют двумя классическими правилами. Первое, modus ponens, заключается в том, чтобы из импликации «Если Р, то Q» и из истинности Р вывести, что истинно также Q. Второе, modus tollens, состоит в том, чтобы из импликации «Если Р, то Q» и из того, что Q ложно, вывести, что Ртакже ложно. Таким образом, формально доказательство — это цепочка рассуждений, которая позволяет получить новые результаты с применением аксиом и правил выведения. Конечным результатом доказательства называется теорема. Если на основе множества аксиом S мы смогли вывести теорему T, обычно это записывается как S ├ T («T доказуемо на основе S»), где знак ├ обозначает синтаксическое отношение выведения или доказательства. Теорией называют множество всех теорем, которые могут быть доказаны. Модель теории — математическая структура, в которой аксиомы истинны, они выполняются. Если М — это модель множества аксиом S, это записывается как М ╞ S («М выполняет S», то есть «аксиомы S истинны в М»). Знак ╞ обозначает семантическое отношение истинности или выполнения. Один из главных вопросов, которые поставил Гильберт, состоит в том, какое математическое отношение существует между отношением доказательства и отношением истинности (между ├ и ╞): истинно ли все доказуемое? Доказуемо ли все истинное?Помимо формулировки аксиом, Гильберт стал первым, кто с чисто математического уровня в основе геометрии поднялся на метаматематический, или метагеометрический, уровень, где рассматриваются свойства любой аксиоматической системы, в частности той, которую он определил для геометрии. Какими свойствами должна обладать аксиома? Гильберт выделил три характеристики: независимость, непротиворечивость и полнота. Аксиоматическая система является независимой, если ни одна аксиома не может быть выведена из другой, то есть если система максимально экономична, не избыточна. И пусть не все сформулированные им аксиомы оказались независимыми (как выяснилось позже), Гильберт доказал независимость между различными группами аксиом. Он утверждал, что аксиома параллельных прямых независима от прочих аксиом, то есть она не может быть выведена на их основе, чем закрыл вопрос, остававшийся открытым несколько столетий. Это стало возможным с применением метода, ставшего вскоре классическим: построить модели геометрий, которые выполняют все желаемые аксиомы, кроме той, независимость которой проверяется, и тогда последняя не может быть следствием из других (поскольку если бы это было так, мы получили бы противоречие — аксиому и ее отрицание). Для доказательства независимости аксиомы параллельных прямых Гильберт создал модель неевклидовой геометрии. А для доказательства независимости аксиомы Архимеда он построил модель неархимедовой геометрии, в которой существуют бесконечно малые величины. Так Гильберт, по примеру Джузеппе Веронезе (1845-1917), распахнул двери для исследования геометрии нового типа.
 Давид Гильберт, 1886 год.
Давид Гильберт, 1886 год.
 Скульптурная группа, воздвигнутая в память о Гауссе и Вебере в Гёттингене. Гильберт опубликовал свои«Основания геометрии» (1899) по случаю ее торжественного открытия.
Скульптурная группа, воздвигнутая в память о Гауссе и Вебере в Гёттингене. Гильберт опубликовал свои«Основания геометрии» (1899) по случаю ее торжественного открытия.
 Кёнигсбергский университет, около 1890 года. Гильберт поступил сюда десятью годами ранее.
Кёнигсбергский университет, около 1890 года. Гильберт поступил сюда десятью годами ранее.
Вторым требованием, которое Гильберт предъявлял к своей аксиоматической системе, была непротиворечивость. Система аксиом является непротиворечивой, если не порождает разногласий, если нельзя вывести никакого противоречия на ее основе. Такую систему аксиом называют когерентной, или совместимой. Модели Бельтрами, Клейна, Пуанкаре и Римана доказали относительную непротиворечивость неевклидовых геометрий в отношении к евклидовой, поскольку эти неевклидовы модели содержались внутри собственно евклидова пространства. Но была ли непротиворечивой евклидова геометрия? Гильберт доказал непротиворечивость евклидовой геометрии относительно арифметики, впервые предложив чисто числовую модель. Он вывел числовое множество, в котором выполняются все геометрические аксиомы, в котором точки — это некоторые пары алгебраических чисел, а прямые — некоторые тройки этих чисел, в котором принадлежность какой-то точки прямой означает, что соблюдается некое числовое уравнение, и так далее. Таким образом, любая противоречивость его аксиоматической системы геометрии привела бы к противоречивости арифметики. Любое противоречие в выводах, cделанных на основе геометрических аксиом, было бы признано арифметическим (например, 0=1).
ВЛИЯНИЕ ГЕРЦА
Не исключено, что Гильберт не был близко знаком с аксиоматическими работами итальянской школы Пеано, зато он знал о достижениях немецкой школы — как в области геометрии (Паш), так и в области механики. Генрих Рудольф Герц (1857-1894) скончался в возрасте 37 лет, но за свою короткую жизнь он успел удивить современников как физик-экспериментатор (он открыл электромагнитные волны и фотоэлектрический эффект) и физик-теоретик. В 1894 году он опубликовал работу «Принципы механики, изложенные в новой связи», в которой аксиоматически изложил знания в этой области. К собственной аксиоматической системе у него имелось два требования: допустимость и корректность. Допустимость совпадает с непротиворечивостью, с отсутствием противоречий. А корректность — с полнотой, с возможностью доказать в рамках этой теории все, что является истинным в мире. Эти два понятия перекликаются с введенными Давидом Гильбертом. Генрих Рудольф Герц, около 1893 года.
Генрих Рудольф Герц, около 1893 года.
Следовательно, Гильберт свел непротиворечивость евклидовой геометрии к непротиворечивости арифметики, что на тот момент было чем-то само собой разумеющимся, хотя вскоре он признал: проблема остается открытой и имеет высокий приоритет (и вскоре мы в этом убедимся). Неевклидовы геометрии основывались на евклидовой, которая, в свою очередь, держалась на арифметике действительных чисел. Как во сне индийского мудреца, мир покоится на спинах слонов, а те стоят на спине черепахи. Ну а черепаха? Вопрос о непротиворечивости арифметики сразу же обрел остроту. В своей книге Гильберт этот вопрос не затронул, тем не менее он считал, что совместимость арифметических аксиом может быть доказана довольно просто (как же он ошибался!). Наконец, третье требование, которое Гильберт выдвинул через несколько лет,— это, по возможности, полнота (хотя она едва намечена в «Основаниях»). Аксиоматическая система называется полной, если в рамках системы мы можем доказать все пропозиции, являющиеся истинными относительно объектов системы, то есть если ни одна из истин не избегает доказательства, если все истины доказуемы. Когда непротиворечивость убеждает нас в том, что все доказуемое верно («все теоремы — истины»), полнота гарантирует нам обратное: все истинное доказуемо («все истины — теоремы»). Если система аксиом, которую он предложил для евклидовой геометрии, была полной, она позволяла вывести все известные ныне и в будущем результаты евклидовой геометрии. Не будем опережать события, но ответ на этот вопрос не был пустяком. В итоге Гильберт убедился, что любая аксиоматическая система, представляющая минимальный интерес, является неполной. В ней истинное не совпадает с доказуемым. Существуют истинные пропозиции, которые не могут быть доказаны. Данная парадоксальная ситуация напоминает положение следователя, который точно знает, кто убийца, но неспособен доказать это. К счастью, в 1951 году польский логик Альфред Тарский (1902-1983) выяснил, что элементарная версия евклидовой геометрии является полной — очевидно, что эта версия не содержит арифметики, поэтому не противоречит знаменитым теоремам о неполноте арифметики Курта Гёделя (1906-1978). Подведем итог. Гильберт предъявлял своей геометрической аксиоматике три требования: независимость, непротиворечивость и полнота. Немецкий математик был убежден, что его аксиоматика минимальна, доказав, в частности, что аксиома параллельных прямых и аксиома Архимеда независимы от прочих. Кроме того, он частично разрешил задачу непротиворечивости, доказав относительную непротиворечивость геометрии арифметике. Таким образом были заложены основы, на которых можно аксиоматически изучать любую геометрию — евклидову или неевклидову, архимедову или неархимедову, — и показано, как можно вывести известные геометрические результаты в зависимости от того, какие группы аксиом приняты.
КРИКИ БЕОТИЙЦЕВ
В письме, адресованном одному коллеге в 1829 году, Гаусс признавался, что в жизни не опубликует ничего по неевклидовой геометрии, так как опасается «криков беотийцев». Немецкий математик намекал на кантианцев, для которых евклидова геометрия была единственно возможной, поскольку единственность пространства предполагала единственность геометрии. Физическое пространство — математическая геометрия. Гаусс не отправил в печать результаты своих исследований, боясь скандала, поскольку открытие неевклидовых геометрий поставило бы под сомнение всю кантианскую философию. Если существует более одной логически мыслимой геометрии, задаваться вопросом об истинности определенной одной — все равно что выяснять, является ли десятичная система более истинной, чем двоичная, а декартова — более истинной, чем полярная. Относительность геометрии подчеркивала, в противовес идеям Канта, что пространство аморфно, и нет смысла спрашивать, какая геометрия истинна. Гаусс был не единственным математиком, испытывавшим антипатию к великому Канту. Георг Кантор признавался, что чтение его работ вызывает у него недомогание, и называл прусского мыслителя «софистом-филистером, который так мало знает о математике». Как и у Гаусса, у Гильберта были свои позитивные и негативные моменты при взаимодействии с одним философом, которые были следствием идей, изложенных им в «Основаниях геометрии». Речь о логике и философе Готлобе Фреге (1848-1925). Этот угрюмый преподаватель Йенского университета считался отцом современной логики (см. главу 4), одним из самых упрямых защитников аксиоматического подхода Античности. Реакция Фреге на книгу Гильберта не заставила себя долго ждать. Так началась переписка, и так стало нарастать недопонимание. В первом письме, отправленном в конце 1899 года, Фреге обрушился на «Основания геометрии» с суровой и педантичной критикой. Раздраженный, но взявший себя в руки Гильберт ответил другим развернутым посланием. В дальнейшем он был более лаконичным, и когда Фреге предложил ему опубликовать переписку, Гильберт категорически отказался. И все же эта полемика представляет собой большой интерес, поскольку демонстрирует открытое столкновение двух концепций аксиоматического метода — старой и традиционной, представляемой Фреге, и новой, начатой Гильбертом. Фреге никогда не оспаривал кантианский анализ геометрии и не допускал никаких других методов, кроме аксиоматического, описанного Аристотелем во «Второй аналитике» и задействованного Евклидом в «Началах». Аксиомы были очевидными истинами, связанными с реальностью. Следовательно, аксиома параллельных прямых была либо истинной, либо нет. Но и того и другого одновременно быть не могло. В одном из писем немецкий философ возмущался: «Никто не может служить двум хозяевам разом: если евклидова геометрия истинна, нужно вычеркнуть неевклидову геометрию из списка наук и поставить ее в ряд с алхимией и астрологией». Позиция ретрограда помешала ему понять, что для Гильберта аксиомы — всего лишь абстрактные схемы, сформулированные с практической целью как начала математической теории. Недовольство Фреге возросло, когда тот прочитал, что Гильберт готов называть «точками», «прямыми» и «плоскостями» любые три произвольных множества, которые удовлетворяли его аксиомам, пусть даже это будут столы, стулья и пивные кружки. Фреге считал, что аксиомы касаются реальных вещей и, следовательно, едва ли у них может быть более одной интерпретации. Гильберт парировал в ответном письме: «Каждая теория — всего лишь набор понятий и некоторых связывающих их отношений, ее базовые элементы могут быть произвольными. Если под точками и прочим я понимаю любую систему вещей, например систему, образованную любовью, законом, щеткой для чистки труб и так далее, и сочту, что для этих вещей все мои аксиомы справедливы, то справедливыми для этих вещей окажутся и мои теоремы, как, например, теорема Пифагора. Другими словами, каждая теория может быть применена к бесконечному числу систем базовых элементов». Когда Фреге опубликовал пару крупных статей, в которых назвал его шарлатаном, через Алвина Корсельта (1864-1947), Гильберт ответил: «Мы можем озаглавить ее как «пустая и бессмысленная игра знаков» или как-то в этом духе; но как законной связи между пропозициями ей не нужно никакое другое специальное название». Любопытно, что употребление терминов в аксиомах смутило и Анри Пуанкаре. Французский математик подключился к критике Гильберта, поскольку ему были неприятны те, кто стремился свести математику к чистым формальным отношениям символов. Он написал подробную рецензию, обвинив немца в мошенничестве, поскольку аксиоматический метод не является созидательным. Этот неоригинальный концептуализирующий инструмент маскирует или прячет то, что должен аксиоматизировать. По мнению Пуанкаре, в «Основаниях геометрии» всегда подразумевается евклидова геометрия, хотя Гильберт это и отрицал. Пусть его аксиоматика и претендует на то, чтобы представлять собой ряд скрытых определений, она происходит из уже существующей теории и ограничивается лишь ее реорганизацией. Французский титан вновь потеснил немецкого титана. Фреге не понял интереса Гильберта к аксиоме полноты линии, или непрерывности прямой, в которой постулируется, что не существует другой большей системы объектов, которая также выполняла бы аксиомы. Философ заявил математику, что это похоже на теологическое заключение на основе аксиомы, которая гласила бы: «Аксиома 3. Существует по крайней мере один Бог». По иронии судьбы Гильберта уже во второй раз обвинили в тяготении к теологии. Однако он был не теологом, а скорее мистиком, поскольку предугадывал будущее математики. Противостояние Фреге и Гильберта, как и в случае с Горданом, — ключ для понимания отличия математики XIX века от математики XX столетия. Для Фреге математическое существование было связано с тем, какие материальные или идеальные объекты существуют в мире. Раз есть только один мир, должна быть только одна геометрия. Аксиоматические системы изначально были пустыми. Гильберт же, наоборот, считал, что аксиомы не просто кодируют поведение математических объектов, но также могут создавать новые математические объекты, если не вступают в противоречие. Следовательно, в математике есть больше одной геометрии, при этом каждая из них непротиворечива (относительно арифметики). «Основания» оказались своего рода знаком ферматы над геометрией, открыв путь другим возможным геометриям (неевклидовым, неархимедовым и так далее). Кроме того, они стали первым столпом современной аксиоматики. С 1900 года, взяв на вооружение новый метод, Гильберт начал внедрять аксиоматизацию в другие научные дисциплины. Раз аксиоматика так хорошо себя показала в геометрии, почему бы ее не задействовать в арифметике, анализе или физике?ГЛАВА 2 Вызов Гильберта
Тень Гильберта покрывает значительную часть математических дисциплин XX века. Когда 8 августа 1900 года он взошел на трибуну II Международного конгресса математиков и взял слово, он предвидел, с какими задачами столкнется математика, и свел их к 23 проблемам, чем решительно повлиял на развитие этой дисциплины. Он поднял завесу, скрывающую будущее математики. Шел 1900 год, начинался новый век. Пока парижане спешили обежать все павильоны Всемирной выставки или поприсутствовать на Олимпийских играх, в Сорбонне, где проходил II Международный конгресс математиков, взял слово Давид Гильберт. Он намеревался говорить не о доказанном, а о том, что оставалось доказать. В тот момент он уже был одним из лучших математиков своего поколения и лидером математической школы в Гёттингене. И хотя эта лекция была прочитана не на пленарном заседании (поскольку Гильберт запоздал с отправкой темы и организаторам пришлось исключить ее из программы), она стала самым запоминающимся докладом на конгрессе. Тридцативосьмилетний Давид Гильберт уже успел показать мощь своих идей. Совершив революцию в теории инвариантов и обратившись к абстракции, он вторгся в теорию чисел и аксиоматическую геометрию и создал работы, которые стали классическими в обеих дисциплинах. Осознавая себя одним из выдающихся математиков, он хотел показать свое проницательное комплексное видение этой науки. Мы можем представить себе нашего героя тем жарким днем 8 августа 1900 года. Высокий, худощавый, с аккуратной бородкой, в своих неизменных очках, он поднялся на кафедру и заговорил. Его основной целью было подчеркнуть, что двигатель прогресса математики — это решение задач, а также бросить вызов математикам XX века.ГИЛЬБЕРТ ПРОТИВ ПУАНКАРЕ
Первый Международный конгресс математиков проходил в Цюрихе тремя годами ранее, в 1897 году. Со своей лекцией «Об отношениях между чистым анализом и математической физикой» французский математик Анри Пуанкаре стал «звездой» этого съезда и в результате возглавил организационный комитет. В Париже Гильберт хотел помериться силами с лидером французской математики. Как и Клейн, он стремился восстановить престиж немецких ученых, но долго сомневался в выборе средств и в итоге запоздал с выбором темы лекции. В своей речи Пуанкаре изложил программу, обозначившую ориентиры развития математики. Целей в ней намечалось три: физическая (дать подходящие инструменты для изучения природы), философская (помочь философу углубиться в понятия числа, пространства и времени) и, наконец, эстетическая, сопоставимая с музыкой или живописью. Математика, отмечал он, имеет ценность сама по себе, а не только как средство, поскольку без теории стопорятся и практическое исследование, и прогресс. Идеальная ситуация, когда физическая и эстетическая цели совпадают. Пуанкаре стремился в деталях показать связь между чистой наукой и ее применением, между анализом и физикой. В условиях этой прагматической обстановки был брошен вызов из 23 проблем математического будущего, сформулированных Гильбертом. Оба ученых были знакомы и восхищались друг другом, но их понимание математики очень разнилось. Немец отстаивал ценность чистой математики. Хотя последующие 20 лет его карьеры была связаны с физикой, он намеревался оспорить некоторые идеи своего французского коллеги. По привычке он посоветовался с Минковским, который через несколько месяцев после первого конгресса написал: «Я перечитал лекцию Пуанкаре и вижу, что все его утверждения так пространны, что им нечего противопоставить [...]. Лучше попробуй заглянуть в будущее и перечислить проблемы, которыми математикам придется заниматься в дальнейшем. Так о твоей лекции будут говорить в последующие десятилетия. Но учти, что у пророчеств есть свои сложности». Следуя совету, лекцию в Париже Гильберт начал с изящных вопросов: «К каким целям будут стремиться лучшие математические умы следующих поколений? Какие новые методы и новые факты в обширной и богатой области математической мысли дадут нам ближайшие столетия?» В основе его речи была переоценка чистой математики через проблемы, которые она сама перед собой ставит. В понимании Гильберта, пока математика предлагает обильное число проблем, она жива и развивается. Отсутствие же проблем говорит об истощении или исчезновении научного ответвления. Наука идет вперед посредством решения проблем. Но каковы характеристики хорошей математической проблемы? Прежде всего, ее должно быть легко сформулировать и объяснить, но сложно решить, хотя и не невозможно, чтобы не тратить силы попусту. Гильберт воспользовался возможностью распространить свою веру в примат аксиоматического метода как механизма определения математических понятий. Когда для Пуанкаре интуитивная догадка и физические аналогии играли основную роль, для Гильберта таковой была чистая логика: строгость и простота. Последнюю треть XIX века он выводил новый математический метод, радикально отличающийся от привычного. Понятие об абстрактной структуре, включая множество, стало новой отправной точкой, новым способом дать определения — скрыто, через аксиомы. Также возникли новые методы доказательства, косвенные или экзистенциальные, и новые способы выражения, потребовавшие использования формальных языков. Это была революция, которая охватывала математику и была многим обязана немецкому ученому. В своей лекции Гильберт вновь вернулся к понятию математического существования: если можно доказать, что свойства, заданные понятию, никогда не приводят к противоречию, то это понятие существует математически. Утверждение было категоричным и шокировало многих его коллег. Он утверждал, что при исследовании оснований науки должна быть сформулирована система аксиом, которая содержала бы точное описание основных отношений между элементарными понятиями этой науки. Таким образом, сформулированные аксиомы стали бы одновременно определениями этих элементарных понятий, и ни одна рассматриваемая научная пропозиция не была бы истинной, если бы не выводилась из аксиом за конечное число логических шагов. Кроме того, философски подводя к своему списку проблем, Гильберт спорил (как и Пуанкаре) с популярными в то время скептиками, вдохновленными физиологом Эмилем Дюбуа-Реймоном (1818-1896) и подхватившим его знамя физиком Пьером Дюгемом (1861-1916). По их мнению, наука подошла к своему пределу, и оставался некий блок вопросов, суть которых, согласно высказыванию Дюбуа-Реймона в 1872 году, «мы не знаем, мы не будем знать» («Ignoramus, ignorabimus!»). Гильберт же с оптимизмом заявлял, что любая математическая проблема решаема — в том смысле, что можно получить положительный или отрицательный ответ. В этом состояло одно из его самых прочных убеждений и мощный стимул для ежедневной работы: «...ибо мы слышим внутри себя постоянный призыв: вот проблема, ищи решение. Ты можешь найти его с помощью чистого мышления, ибо в математике не существует ignorabimus». К сожалению, оказалось, что это не так. Как известно, эта идея в 30-е годы получила сильный удар.ВЫЗОВ ГИЛЬБЕРТА
Гильберт предложил 23 математические проблемы, но ввиду временных ограничений в своей лекции он упомянул только десять из них. Однако он предоставил присутствующим печатный вариант лекции, который сразу же был растиражирован в Германии и Франции. Разберем эти 23 проблемы (наиболее простые и понятные будут рассмотрены подробно). Проблемы можно сгруппировать в несколько блоков в зависимости от предмета, к которому они относятся: основания математики (проблемы 1, 2, 3, 4 и 5) и математической физики (проблема 6), теория чисел (проблемы 7, 8, 9, 10 и 11), алгебра (12, 13, 14 и 17), геометрия (15, 16, и 18) и анализ (19, 20, 21, 22 и 23). Основания математики, геометрия и алгебра с различных углов зрения, теория чисел и анализ представлены в списке наряду с другими вопросами спорной классификации. В первом блоке приведены проблемы оснований математики и физики. 1. Проблема континуума (см. главу 4). Доказать истинность или ложность знаменитой континуум-гипотезы Кантора: не существует подмножества на числовой прямой, кардинальное число которого (то есть его размер) находилось бы строго между кардинальном числом рациональных чисел и кардинальным числом действительных чисел. Поставив этот вопрос как первую математическую проблему будущего, Гильберт занял позицию абстрактной теории множеств в пику ее многочисленным врагам. 2. Проблема непротиворечивости аксиом арифметики. Этот вопрос был крайне важен, поскольку положительный ответ косвенно доказал бы непротиворечивость всей математики. В «Основаниях геометрии» Гильберт оставил эту проблему, но в 1920-е годы вернулся к ней уже как исследователь. К сожалению, в 1931 году австрийский логик Курт Гёдель доказал, что формально эта проблема неразрешима. Невозможно доказать непротиворечивость аксиом арифметики. 3. Равенство объема двух тетраэдров одинакового основания и высоты. В своей книге Гильберт озаботился определением понятия площади в плоскостной геометрии без использования анализа бесконечно малых (интегралов) и достиг успеха, охарактеризовав многоугольники одинаковой площади как равносоставленные (то есть состоящие из одного и того же числа одинаковых треугольников). Удастся ли сделать то же самое с понятием объема в пространственной геометрии? Удастся ли охарактеризовать многогранники одинакового объема как многогранники, которые могут быть разложены на одно и то же число равных тетраэдров? В 1902 году Макс Ден (1878-1952) ответил на эти вопросы отрицательно: существует два тетраэдра с одинаковым основанием и высотой (а значит, с одинаковым объемом), которые, однако, не являются равносоставленными. Невозможно разделить первый на конечное количество многогранных частей так, чтобы они могли быть собраны для получения второго. В то время как в двух измерениях было возможно определить площадь, не применяя анализ, в трех измерениях сложный процесс перехода к пределу, известный как чертова лестница, оказывался неизбежным и мешал определить понятие объема, не прибегая к анализу. 4. Проблема отрезка прямой как кратчайшего расстояния между двумя точками. Гильберт предлагает продолжить исследование различных возможных аксиоматических геометрий с учетом того, к какой группе аксиом может привести результат, позволяющий сделать вывод, что в любом треугольнике сумма двух его сторон всегда больше третьей, а следовательно, отрезок прямой — это кратчайший путь между двумя точками. Хотя эта проблема сформулирована слишком расплывчато, она стала более точной в области геометрии Римана, когда требуется построить все возможные расстояния так, чтобы обычные прямые линии оказались геодезическими (кратчайшими путями). Математический клуб Гёттингена, 1902 год. В центре Клейн, основатель клуба, справа от него Г ильберт.
Математический клуб Гёттингена, 1902 год. В центре Клейн, основатель клуба, справа от него Г ильберт.
 Математик Герман Минковский в молодости. С Гильбертом их связывала крепкая дружба до самой смерти Минковского в 1909 году.
Математик Герман Минковский в молодости. С Гильбертом их связывала крепкая дружба до самой смерти Минковского в 1909 году.
 Гильберт и Кёте Ерош, на которой он женился в 1892 году.
Гильберт и Кёте Ерош, на которой он женился в 1892 году.
5. Анализ понятия, введенного Софусом Ли (1842-1899) в отношении группы трансформаций, за исключением гипотезы о дифференцируемости функций, входящих в состав группы. 6. Математический подход к аксиомам физики. Гильберт был заинтересован в аксиоматизации различных областей физики (в особенности механики и вычисления вероятностей, которое в то время набирало силу как инструмент термодинамики), чтобы определить им формат, наподобие геометрии, ведь ее он считал практически эмпирической наукой. В решении этой проблемы уже наметился сдвиг благодаря физикам Эрнсту Маху (1838-1916) и Генриху Герцу, но математики ею еще не занимались. Программа аксиоматизации физики добилась (как станет ясно в следующей главе) определенных побед в первые десятилетия XX века. В рамках блока теории чисел Гильберт выделил пять проблем. 7. Иррациональность и трансцендентность некоторых чисел. Трансцендентное число — это тип иррационального числа, которое не является корнем из какого-либо многочлена с целыми коэффициентами. В противоположность ему алгебраическое число — это любое число, являющееся решением полиномиального уравнения с целыми коэффициентами. Поскольку было известно не так уж много трансцендентных чисел (кроме π и e), Гильберт сформулировал конкретный вопрос: если a — это алгебраическое число (отличное от 0 и 1), а b — иррациональное алгебраическое число, является ли аь трансцендентным? Для Гильберта это было одной из самых сложных проблем в списке. Однако в 1934 году Александр Гельфонд (1906-1968) и Теодор Шнайдер (1911— 1988) доказали, что это так. В частности, √2√2 является трансцендентным. 8. Изучение простых чисел. Здесь Гильберт поставил ряд вопросов, связанных с распределением простых чисел. Главный вопрос — без сомнения, знаменитая гипотеза Римана, в которой предполагалось, что некоторая функция, связанная с этими числами и называемая дзета- функцией Римана ζ(z), имеет все свои нули на прямой Re(z) = ½ комплексной плоскости, то есть все ее нули — комплексные числа с действительной частью, равной ½. На сегодняшний день она все еще не доказана, хотя с помощью компьютера было проверено, что первые 1,5 триллиона нулей выполняют эту гипотезу. Гильберт также упомянул гипотезу Гольдбаха (согласно которой любое четное число может быть выражено в виде суммы двух простых чисел), существование бесконечного числа простых чисел-близнецов (то есть простых чисел, разность между которыми равна 2) и так далее. 9. Доказательство наиболее общего закона взаимности в любом числовом поле. 10. Определение разрешимости диофантовых уравнений. 11. Исследование квадратичных форм с произвольными алгебраическими коэффициентами. В блоке алгебры — следующие проблемы. 12. Распространение теоремы Кронекера об абелевых полях на произвольную алгебраическую область рациональности. 13. Невозможность решения общего уравнения седьмой степени с помощью функций, зависящих только от двух переменных. 14. Доказательство конечности некоторых полных систем функций. 17. Представление определенных форм в виде сумм квадратов. В блоке геометрии... 15. Строгое обоснование исчислительной геометрии Германа Шуберта (1848-1911).
ДЕСЯТАЯ ПРОБЛЕМА ГИЛЬБЕРТА
Это одна из значительных проблем, которая кажется простой, хотя это не так. Заключается она в поиске общего способа, позволившего бы выяснить, имеет ли диофантово уравнение целые решения или нет, без необходимости вычислять их. Диофантовы уравнения — это уравнения, в которых участвует только один многочлен с целыми коэффициентами и нужно найти все целые решения. Уравнения носят имя греческого математика Диофанта (III век), ими занимавшегося. В частности, знаменитое уравнение xn+yn=zn последней теоремы Ферма — это диофантово уравнение (в 1995 году Эндрю Уайлсу (р. 1953) удалось доказать, что у этого уравнения нет целых решений, отличных от нуля, если п больше 2). Проблема оставалась открытой, пока в 1970 году теория чисел и математическая логика не объединились: советский математик Юрий Матиясевич (р. 1947), следуя идеям Мартина Дэвиса (р. 1928), Хилари Патнем (р. 1926) и Джулии Робинсон (1919-1985), смог доказать, что такого алгоритма не существует. Перенесшая операцию на сердце Джулия Робинсон на свой день рождения обычно загадывала желание: «Пусть кто-нибудь решит десятую проблему Гильберта. Я не успокоюсь, пока ответ не будет найден». Любопытно, что ее старшая сестра Констанс Рейд (1918-2010) написала лучшую биографию Давида Гильберта.16. Исследование топологии алгебраических кривых и поверхностей, включая (как отсылку к работе Пуанкаре) изучение числа и формы предельных циклов, являющихся решениями некоторых дифференциальных уравнений.
 Слева — замощение плоскости шестиугольниками. Справа — замощение пространства усеченными октаэдрами.
Слева — замощение плоскости шестиугольниками. Справа — замощение пространства усеченными октаэдрами.
18. Построение пространства на основе конгруэнтных многогранников. Будучи одной из классических проблем математики, известная как проблема паркета или бордюра, она состоит в том, чтобы определить, сколькими различными способами можно целиком заполнить плоскость одинаковыми геометрическими фигурами. Гильберт расширил ее, рассмотрев возможность заполнения пространства конгруэнтными многогранниками (см. рисунок). Так что речь шла об обобщении уже произведенного исследования групп симметрии и замощений (многие из них представлены в мозаике архитектурного ансамбля Альгамбры) двумерной плоскости до случая трехмерного пространства. Промежуточные достижения в этой области пришлись на 1910 год и принадлежат Людвигу Бибербаху (1886-1982) — математику, который в итоге присоединился к нацистской партии и сместил Гильберта. Кроме того, в этот раздел Гильберт включил знаменитую гипотезу Кеплера: какое расположение шаров одного радиуса оставляет меньше всего свободного пространства? Решение Кеплера — расположить их подобно апельсинам в корзине, как совсем недавно продемонстрировал Томас Хейлс (р. 1958). И наконец, в блоке, посвященном анализу, находились последние пять проблем. 19. Изучение аналитичности решения регулярных задач вариационного исчисления. 20. Изучение существования решений задач вариационного исчисления с определенными граничными условиями. 21. Доказательство существования линейных дифференциальных уравнений с заданной группой монодромии. 22. Униформизация аналитических зависимостей с помощью автоморфных функций (проблема, происхождение которой лежало в работах Клейна и Пуанкаре по данному вопросу). 23. Развитие методов вариационного исчисления. Гильберт значительно способствовал прогрессу в этой области анализа (которая была напрямую связана с проблемами 19 и 20, касающимися существования, единственности и свойств решений вариационного исчисления). Эта тема обладала чрезвычайной жизнеспособностью в XX веке, что говорит об отличном чутье Гильберта, закончившего список проблем общим вопросом из этой области. В Париже, не имея достаточно времени, Гильберт успел обозначить только 10 из своих 23 проблем: континуум-гипотезу (проблема 1); непротиворечивость арифметики (2); аксиоматизацию физических теорий (6); некоторые проблемы теории чисел, включая гипотезу Римана (7 и 8); невозможность разрешения уравнения седьмой степени (13); вопрос о кривых и поверхностях, определенных полиномиальными уравнениями (16); аналитические решения регулярных проблем вариационного исчисления (19); существование обыкновенных дифференциальных уравнений, соответствующих заданным группам монодромии (21), и вопрос Пуанкаре о параметризации алгебраических кривых с помощью автоморфных функций (22).
Если бы я проснулся, проспав тысячу лет, то в первую очередь спросил бы: доказали ли гипотезу Римана? Давид Гильберт
Не так давно историк математики Тиле Рюдигер в одной из тетрадей Гильберта обнаружил, что тот хотел добавить еще одну проблему (24), которую в итоге отверг. Проблема состояла в определении критерия простоты или доказательства максимальной простоты некоторых доказательств. Гильберт намеревался развить общую теорию ометодах доказательства в математике. Как ни парадоксально, через несколько лет он сам основал (см. главу 5) теорию доказательств. Однако в списке был ряд важных упущений: несколько путей, по которым он не пошел. Матричная алгебра, статистика, логика или прикладная математика, бурно развивавшиеся в конце века, наряду с зарождающимися топологией, теорией меры и функциональным анализом для Гильберта интереса не представляли. Точно так же проблема трех тел и последняя теорема Ферма были упомянуты, но не предложены в качестве открытых проблем математики будущего.
В следующей таблице показано современное состояние 23 проблем Гильберта.
| Проблема | Описание | Состояние |
| 1 | Континуум - гипотеза | Курт Гёдель (1938) и Пол Коэн (1963) доказали ее неразрешимость как истинную или ложную на основе стандартного набора аксиом теории множеств |
| 2 | Непротиворечивость аксиом арифметики | Курт Гёдель (1931) доказал, что установление неп роти вореч и вости арифметики является формально неразрешимой проблемой |
| 3 | Определение понятия объема без применения анализа | Опровергнута Максом Деном (1902) |
| 4 | Перечисление всех метрик, прямые линии которых являются геодезическими | Положительно решена Алексеем Погореловым (1975) |
| 5 | Дифференцируются ли непрерывные группы автоматически? | Положительно решена Эндрю Глизоном (1952) |
| 6 | Математическое изложение аксиом физики | Частично решена: |
| — механика: Георг Гамель (1909); | ||
| — термодинамика: Константин Каратеодори (1909); | ||
| — специальная теория относительности: Альфред Робб (1914) и Константин Каратеодори (1923); | ||
| — квантовая механика: Джон фон Нейман (1932); | ||
| — теория вероятностей: Андрей Колмогоров (1933) | ||
| 7 | Является ли ab трансцендентным, если a≠0,1 алгебраическое и b иррациональное алгебраическое? | Решена независимо Александром Гельфондом и Теодором Шнайдером (1934) |
| 8 | Гипотеза Римана и гипотеза Гольдбаха | Не решена |
| 9 | Доказательство наиболее общего закона взаимности в любом числовом поле | Решена Эмилем Артином (1923) |
| 10 | Найти универсальный алгоритм диофантовых уравнений | Отрицательно решена Матиясевичем (1970) |
| Проблема | Описание | Состояние |
| 11 | Решение квадратичных форм с алгебраическими числовыми коэффициентами | Частично решена Хельмутом Хассе (1923) и Карлом Зигелем (1930) |
| 12 | Распространение теоремы Кронекера | Не решена |
| 13 | Решение общего уравнения седьмой степени с помощью функций, зависящих только от двух переменных | Отрицательно решена Арнольдом и Колмогоровым (1957) |
| 14 | Доказательство конечности некоторых полных систем функций | Отрицательно решена через контрпример Масаеси Нагатой (1959) |
| 15 | Строгое обоснование исчислительной геометрии Шуберта | Отрицательно решена Бартелем ван дер Варденом (1930) |
| 16 | Топология алгебраических кривых и поверхностей | Не решена |
| 17 | Представление определенных форм в виде квадратов | Решена положительно Эмилем Артином (1927) и Георгом Крайзелем (1957) |
| 18 | Гипотеза Кеплера | Решена Томасом Хейлсом (2005) |
| 19 | Всегда ли решения регулярных задач вариационного исчисления аналитические? | Утвердительно решена Сергеем Бернштейном (1904) |
| 20 | Всели задачи вариационного исчисления с определенными граничными условиями имеют решение? | Решена в течение XX века |
| 21 | Доказательство существования линейных дифференциальных уравнений с заданной группой монодромии | Отрицательно решена Дмитрием Аносовым и Андреем Болибрухом (1989) |
| 22 | Униформизация аналитических зависимостей с помощью автоморфных функций | Решена независимо Паулем Кёбе и Анри Пуанкаре (1907) |
| 23 | Развитие методов вариационного исчисления | Решена в течение XX века |
18 ПРОБЛЕМ СМЕЙЛА И 7 ПРОБЛЕМ ТЫСЯЧЕЛЕТИЯ
В 1992 году Международный математический союз принял на себя инициативу связать лекцию Гильберта 1900 года с современным состоянием математики. Несмотря на огромные достижения математики XX века, дюжины примечательных проблем еще ждут своего решения. В 2000 году лауреат Филдсовской премии Стивен Смейл (р. 1930) составил список из 18 проблем, актуальных в XXI веке. Первые три — это гипотеза Римана, гипотеза Пуанкаре (знаменитый топологический вопрос, поставленный в 1904 году) и проблема Р = NP (любая ли проблема, решаемая в экспоненциальном неполиномиальном времени, имеет альтернативное решение в полиномиальном времени?). Одновременно институт Клея назначил семь премий в один миллион долларов для каждой из обозначенных проблем тысячелетия. Некоторые из них новые, другие — старые знакомые, уже более 100 лет ожидающие решения. Среди этих задач, естественно, три указанные выше проблемы, а также проблема существования решений уравнений Навье — Стокса (которые описывают движение флюидов). В 2002 году российский математик Григорий Перельман (р. 1966) доказал одну из них — гипотезу Пуанкаре.УЧИТЕЛЬ И УЧЕНИКИ
Сегодня, спустя более чем 100 лет, можно констатировать хорошие результаты: больше половины проблем решены, хотя некоторые решены довольно неожиданно. Часть из них все еще остаются открытыми (это случай проблемы 8 — гипотезы Римана, «звезды» списка) или частично открытыми (случай проблем И, 12 и 16). Проблемы, которые Гильберт определил для нового века, не остались без внимания, они заворожили несколько поколений математиков, породив настоящий поток исследовательских статей. Решить проблему Гильберта — задача, достойная уважения, способствующая карьере. Математик, решивший одну из этих проблем, занимал «почетное положение в математическом сообществе», говоря словами Германа Вейля (1885-1955) из некролога Гильберту. Это был случай свершившегося пророчества. Несмотря на то что присутствующих на лекции Гильберта было не так много (доподлинно неизвестно, был ли там Пуанкаре, к которому отсылали некоторые из этих проблем), она не вызвала оживленной дискуссии (за исключением столкновения с Пеано, напомнившего Гильберту о работах итальянских математиков в области второй проблемы), репутация их автора и стоявшего за ним Гёттингенского центра сделали свое дело. Математическими проблемами будущего стали именно те, которые Гильберт обозначил в своей программе, потому что этому способствовала его харизма. Однако предложения Пуанкаре также исполнились: например, развитие функционального анализа, который стольким обязан Гильберту, шло параллельно развитию квантовой механики. И когда сошла на нет тенденция к абстракции и аксиоматическим структурам, характерная для начала XX века, произошел скачок прикладной математики (исследование операций, теория хаоса и так далее), который был знаком уважения французскому математику. Гильберт поставил свою метку на целую эпоху математики. Однако причина того, почему он вызывал восхищение у людей, не исчерпывалась его исследованиями. Гаусс и Риман, также из Гёттингена, были математиками более высокого уровня, чем Гильберт, но их влияние на современников было гораздо меньшим. Гильберт, как гамельнский крысолов, увлек многих математиков за собой в глубокую реку чистой математики. Успех проблем Гильберта в качестве исследовательской программы кроется в той ауре, которую он создал вокруг себя. Другими словами, оценить его влияние можно, только осознав, что он был не просто трудолюбивым преподавателем. Гильберт излучал заразительный энтузиазм, побуждал обмениваться научными идеями в ходе разговоров или долгих прогулок. Краеугольным камнем его математической деятельности было сочетание исследования и обучения. Отто Блюменталь (1876— 1944), первый из 69 учеников, которые написали докторскую диссертацию под его руководством, спустя 40 лет делился впечатлением, которое произвел на него прибывший в Гёттинген Гильберт: «По сравнению с прочими преподавателями этот проворный мужчина с густой рыжей бородой и в повседневном костюме выглядел не слишком академично. Его лекции были очень лаконичными. Он читал их довольно скучно, но благодаря богатому содержанию и ясности представления о форме можно было забыть. Гильберт часто демонстрировал свои новые открытия, но всегда убеждался, что все следят за его мыслью. Он читал лекции для учеников, а не для самого себя».ПОРТРЕТ ГИЛЬБЕРТА В ШЛЯПЕ
Эта фотография 1912 года стала частью собирательного образа математиков. Панама, глаза, сверкающие за стеклами очков, заостренная бородка. .. Но кое-что отсутствует на этом известнейшем портрете: обворожительность персонажа. Непреодолимая страсть к математике, о которой свидетельствует цветущая риторика его речей, и некоторая чудаковатость, свойственная ученым. Один из учеников рассказывал, как несколько дней Гильберт появлялся на людях в одних и тех же рваных брюках, отчего окружающим становилось неловко. Указать ему на эту деликатную деталь было поручено его помощнику, Рихарду Куранту (1888-1972). Однажды вечером, воспользовавшись тем, что они проходят мимо колючих кустов, Курант сообщил Гильберту, что у него порвались брюки. «А! Нет, — ответил Гильберт, — они уже несколько недель в таком виде, но никто не обратил внимания». Более того, обычно разъезжая на велосипеде по улицам Гёттингена, этот математик никогда не уставал флиртовать. На одной из вечеринок по случаю дня рождения гости состязались в стихосложении, каждая строфа начиналась с первой буквы имени девушки, за которой ему доводилось ухаживать. Но когда веселая компания добралась до буквы К, никто не знал, что сказать. В этот момент Кёте, благоразумная и мудрая жена Гильберта, заметила: «Могли бы хоть раз подумать и обо мне».
Естественно, весомыми были и обстоятельства времени и места. После смерти старого Кронекера и отставки Вейерштрасса немецкий академический мир начал оживать, академические кафедры закружились в танце, в результате Клейн и Гильберт заняли благоприятное положение и обосновались в Гёттингене. Вскоре стараниями Феликса Клейна, большого ученого и политика, Гёттинген превратился в важнейший математический центр мира, обладающий впечатляющей группой преподавателей, среди которых выделялись Гильберт и Минковский (в штат университета его зачислили в 1902 году), а также многочисленными подающими надежды учениками. За 35 лет преподавания в Гёттингене было сделано очень многое. Список учеников Гильберта впечатляет: Отто Блюменталь, Макс Ден, Эрхард Шмидт (1876-1959), Рихард Курант, Эрнст Цермело (1871-1953), чемпион мира по шахматам Эмануэль Ласкер (1868-1941) и другие. Среди них выделяется Герман Вейль, он защитил докторскую диссертацию под руководством Гильберта в 1908 году и сменил его в 1930 году, когда тот вышел в отставку. Гильберт всегда держался как наставник, помогающий по мере возможности. Так, например, когда возникло недовольство по поводу назначения преподавателем в университете молодой выдающейся женщины-математика Эмми Нётер (1882-1935), своим самым неуступчивым коллегам Гильберт иронично заявил: «Не думаю, что пол кандидата является аргументом против его назначения. Все-таки это университет, а не общественная баня». Это еще один пример широты его взглядов.
ГЛАВА 3 Аксиоматизация физики
Первые годы нового века Гильберт работал в области вариационного исчисления и интегральных уравнений. Ему удалось придать форму новому ответвлению анализа — функциональному анализу. Кроме того, он сыграл ключевую роль в математической формулировке общей теории относительности и квантовой механики. Гильберт соревновался с Эйнштейном в поиске уравнений, которые связали бы гравитацию с теорией относительности. Но это не все: так называемое гильбертово пространство стало в итоге математической структурой, распахивающей двери в квантовое пространство. Одно из недавних открытий в области истории математики касалось безудержного интереса, который Гильберт проявлял к физике своего времени. Дружба с Минковским и знакомство с работами Герца оказались катализаторами его интереса в юные годы, а математическая традиция Гёттингена, без сомнения, сделала все остальное (Гаусс, Риман и Клейн разделяли его любовь к физике). Его научная деятельность совпала с рождением двух физических учений XX века — квантовой теории (1900) и теории относительности (1905), — что усилило его интерес в первые два десятилетия нового века. С приезда в Гёттинген в 1895 году Гильберт вел множество курсов и семинаров, посвященных математической физике. Неудивительно, что на лекции в Париже в 1900 году, говоря о шестой проблеме, он отметил: исследования в области оснований геометрии подсказывают тот же — аксиоматический — подход к физическим наукам, в которых у математики заметная роль. Механика, оптика, а также термодинамика и теория электричества должны следовать скрупулезной модели, испробованной геометрией. Строгость — не сугубо математическое свойство. Физика может достичь абсолютной строгости по стандартам аксиоматического метода. В 1905 году, избрав это направление, немецкий математик предложил аксиоматическое изложение механики, описав понятие силы через различные аксиомы векторного пространства. Затем он аксиоматизировал теорию вероятностей — в том виде, в каком она возникла в рамках кинетической теории газов. Ряд выпускников Геттингена, учеников Гильберта, внесли в это существенный вклад. В 1909 году Георг Гамель (1877-1954) аксиоматизировал классическую механику, а Константин Каратеодори (1873-1950) сделал то же для термодинамики. Сам Гильберт совершил гигантский шаг, в 1915 году сформулировав собственные уравнения для общей теории относительности. Наконец, в конце счастливых 1920-х годов в сотрудничестве с Лотаром Нордгеймом (1899-1985) и Джоном фон Нейманом (1903-1957) он попытался включить квантовую механику в аксиоматическую систему. Однако его интерес к физике не может рассматриваться в отрыве от анализа. Его внимание к анализу сменялось вниманием к физике и обратно, и в первые два десятилетия века это происходило непрерывно. Гильберт сосредоточился на двух областях, довольно близких к анализу, — вариационном исчислении и интегральных уравнениях. Действительно, в 3 из 23 проблем, которые Гильберт представил в Париже, речь шла о вариационном исчислении и, в частности, о развитии теории уравнений в частных производных.УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
Довольно долгое время уравнения (алгебраические) отвечали требованию вычислять неизвестные числа, например корни многочлена. Но в математике нередко возникают качественно другие проблемы: те, в которых неизвестное — это не число, а функция, выражающая отношение между различными переменными (как в случае с движением планет — зависимость пространственных координат от времени). Особый класс здесь — так называемые дифференциальные уравнения, определяющие неизвестную функцию на основе одного или нескольких уравнений, в которых участвуют производные функции. Основав исчисление (дифференциальное и интегральное), Ньютон сформулировал законы физики в том виде, который связывал между собой физические величины и скорости изменения. То есть пространство, пройденное движущимся телом с его скоростью, и скорость движущегося тела с его ускорением. Итак, законы физики оказались выраженными через дифференциальные уравнения, при этом дифференциалы и производные были мерами скорости изменения. Производная функции показывает, как изменяется значение функции, если она возрастает, убывает или остается постоянной. Ускорение, например, измеряет изменения скорости движущегося тела, вариацию скорости во времени, поскольку частное дифференциалов скорости и времени есть производная скорости относительно времени: а = dv/dt Однако решение дифференциальных уравнений, как и алгебраических, не всегда оказывается простым, вернее никогда. Если неизвестная функция зависит от единственной переменной, они называются обыкновенными дифференциальными уравнениями. Например, производная от функции синуса у = sin х равна у’ = cos х, где у’ обозначает первую производную. Эта последняя функция может быть дифференцирована, в свою очередь, для получения у" = -sin х> из чего можно вывести дифференциальное уравнение у" = -у. Это — дифференциальное уравнение второго порядка, поскольку появляется вторая производная. Другой пример дифференциального уравнения второго порядка — второй закон Ньютона: F = m x а («сила равна произведению массы на ускорение»), а = dv/dt = d²x /dt², где ускорение — это первая производная от скорости, но также вторая производная от положения, если x(t) обозначает положение движущегося тела в зависимости от времени. Обратная ситуация — если неизвестная функция зависит от более чем одной переменной и появляются производные относительно этих переменных: это называется уравнениями в частных производных. Предположим, объем газа V — это функция от его температуры Т и давления на него Р, то есть V(T,Р). Когда Тили Р изменяются, V тоже изменяется. Производная V(T, Р) относительно Т называется частной производной относительно Т и записывается как ∂V(T,Р)/∂T. Точно так же ∂V(T,Р)/∂P является частной производной относительно Р. Как и в случае с обыкновенными производными, существуют вторая, третья и так далее частные производные; так, в качестве примера ∂2V(T,Р)/∂P2 представляет собой вторую частную производную относительно Р. Но дифференциальные уравнения, в которых участвуют частные производные, имеют особенные черты, принципиально отличающие их от обыкновенных. В изучении естественных явлений уравнения в частных производных появляются так же часто, как и обыкновенные дифференциальные уравнения, но обычно их намного сложнее решать. В XVIII веке изучение физического явления в сущности было примерно тем же самым, что и нахождение дифференциального уравнения, которое им управляет. Так, после открытия Ньютоном знаменитого дифференциального уравнения «сила равна произведению массы на ускорение», которое управляет движением систем точек и твердых упругих тел, швейцарский математик Леонард Эйлер (1707-1783) сформулировал систему уравнений в частных производных, описывающую движение сплошных сред (воды, воздуха и других флюидов), не обладающих вязкостью. Через некоторое время французский математик Жозеф-Луи Лагранж (1736-1813) сосредоточился на музыке, на уравнении в частных производных, которое показывает распространение звуковых волн. Позже Жан-Батист Фурье (1768-1830) обратился к потоку тепла, предложив другое уравнение в частных производных, описывающее его распространение. В разгаре XIX века уравнения Навье — Стокса описало движение вязких флюидов, а уравнения Максвелла — электромагнетизм. Вся природа — твердые тела, флюиды, звук, тепло, свет, электричество — оказалась смоделированной посредством уравнений в частных производных. Но одно дело — найти уравнения рассматриваемого явления, а другое — решить их.Физика слишком сложна для физиков. Давид Гильберт
Парадигматические уравнения в частных производных — это три уравнения, полученные в области математической физики: уравнение волн, уравнение тепла и уравнение Лапласа. Прежде чем рассмотреть последнее, введем обозначение, которое чрезвычайно упрощает его запись: лапласианом функции u = u(х,y,z,t) от пространственных координат и времени называют сумму следующих производных относительно х,y,z: ∆u = ∂²u/∂x² + ∂²u/∂y² + ∂²u/∂z² Эту группу частных дифференциалов лапласианом назвал Джеймс Клерк Максвелл (1831-1879), хотя обозначение заглавной греческой буквой дельта восходит к трактату 1833 года. В данных обстоятельствах ∆u = 0 — это уравнение Лапласа, или уравнение непрерывности, выражающее, что идеальный флюид, в котором нет завихрений, неразрушим. Это уравнение математически кодирует прописную истину: если флюид несжимаем, из сколь угодно малого объема в момент времени должно выйти столько же жидкости, сколько ее содержится в нем. Однако французский математик и физик Пьер-Симон Лаплас (1749-1827) обнаружил его в небесной механике, изучая гравитационный потенциал, то есть функцию, измеряющую гравитационную силу, с которой тело — какой бы формы оно ни было — притягивает внешнюю точечную частицу. В результате это уравнение Лапласа также получило название уравнения потенциала. Как уже можно догадаться, один из гениальных вкладов Гильберта в анализ был связан со строгим решением этого уравнения в частных производных.
УРАВНЕНИЕ ВОЛН И УРАВНЕНИЕ ТЕПЛА
Уравнение волн, которое описывает распространение волн звука или света, а также физических волн, производимых колеблющейся струной или мембраной, следующее: ∂²u/∂t² = c²∆u . В свою очередь, уравнение тепла, которое регулирует распространение тепла (то, как оно движется из зон, где температура выше, в зоны, где она ниже), соответствует следующему виду: ∂u/∂t = k∆u . Оба уравнения кажутся обманчиво похожими, за исключением того, что в первом вместо первой производной появляется вторая производная относительно времени. Эта тонкая математическая разница имеет чрезвычайное значение для физики: уравнение волн обратимо — в том смысле, что оно остается неизменным, если мы изменим направление течения времени. Математически: если мы заменим t на -t, уравнение останется прежним, поскольку при двойном дифференцировании знаки отрицания взаимно уничтожаются. Следовательно, уравнение не упорядочивает решения с течением времени, в связи с чем можно восстановить информацию о прошлом (по этой причине мы используем световые или звуковые сигналы для общения). Уравнение тепла, наоборот, необратимо (если заменить t на -t, мы не получим то же самое уравнение). Распространение тепла ориентировано темпорально, оно зависит от оси времени. Эта необратимость проявляется в том, что уравнение упорядочивает решения стечением времени, поэтому обычно невозможно восстановить информацию о прошлом (решение, соответствующее пику тепла, в итоге смягчается таким образом, что через некоторое время невозможно узнать, где и как возник взрыв или пожар, поскольку тепло распространилось по всему пространству).ОТ ПРОБЛЕМЫ К ПРИНЦИПУ ДИРИХЛЕ
Одной из проблем уравнения Лапласа, которая не давала покоя математикам и физикам XIX века, была так называемая проблема Дирихле, названная в честь немецкого математика Петера Густава Лежёна Дирихле (1805-1859). Она состояла в том, чтобы найти гармоническую функцию в области пространства, то есть функцию u, удовлетворяющую уравнению Лапласа Δu = 0 в этой области пространства, при этом на границе области (см. рисунок 1) она принимает заданные значения (например, u = ƒ на границе). То есть если обозначить область как Ω и границу области как γ, Δu = 0 в Ω u = ƒ в γ РИС. 1
В проблеме Дирихле ищут функцию и, которая принимает определенные значения на границе, и лапласиан, которой равен нулю внутри области.
РИС. 1
В проблеме Дирихле ищут функцию и, которая принимает определенные значения на границе, и лапласиан, которой равен нулю внутри области.
Эта математическая проблема была связана со множеством физических проблем. Одна из них заключалась в ее решении. Представим себе упругую мембрану, равномерно растянутую над областью плоскости Ω, ограниченную кривой γ. Теперь предположим, что контур деформируется так, что каждая точка γ занимает некоторый уровень, заданный функцией ƒ. Естественно, вследствие деформации контура мембрана изогнется и начнет колебаться. Если позволить ей свободно колебаться, по истечении некоторого времени она достигнет равновесия, приняв некоторое положение (см. рисунок 2). Требуется вычислить величину деформации каждой точки внутри мембраны относительно плоскости, то есть высоту, которую сейчас занимает то, что переместилось. Функция u(х, у), измеряющая эти величины, соответствует проблеме Дирихле (в двух измерениях). С точки зрения физики должна существовать функция u, являющаяся решением проблемы, кроме того, она должна быть единственной, поскольку рано или поздно мембрана остановится, и произойдет это единственным способом. Однако математически вопрос не настолько очевиден. В лекциях по данной теме Дирихле — как и Гаусс, Джордж Грин (1793-1841) и Уильям Томсон (1824-1907) — разработал метод решения проблемы и нахождения неизвестной функции и. Риман позже назвал этот метод принципом Дирихле. Дирихле допустил, что в положении стабильного равновесия решение — функция u — должно обладать наименьшей энергией, то есть давать наименьшее значение для следующего интеграла {энергия Дирихле):
 РИС. 2
Возможное положение равновесия мембраны через некоторое время.
РИС. 2
Возможное положение равновесия мембраны через некоторое время.
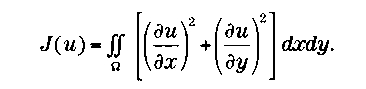
Другими словами, функция, которую мы ищем, должна давать — в сравнении со всеми возможными функциями, определяющими то же самое граничное условие, — наименьшее возможное значение для энергии. На физических основаниях оказывается возможным, что при любой заданной замкнутой кривой в пространстве существует поверхность с наименьшей энергией, которая ее заполняет, поскольку любая поверхность или мембрана будет стремиться принять конфигурацию, требующую наименьшей энергии. Так как интегрируемое J(u) всегда положительно (является суммой квадратов), интеграл J(u) всегда больше или равен нулю. Поэтому Дирихле показалось рациональным, что должна существовать функция u, которая имела бы наименьшее значение. Заметьте, что если бы не было этой нижней границы, предполагающей нуль, могло бы оказаться так, что получаемые значения с каждым разом становились бы все меньше (0, -1, -2, -3...), причем это необязательно должно быть наименьшее значение. Предполагая существование этой минимизирующей функции u из J(u)> Дирихле доказал, что функция u гармоническая и, следовательно, удовлетворяет исходной проблеме, которую нужно решить. Но оставалось неясно, действительно ли существует этот минимум, эта функция u, в которой интеграл Дирихле достигал бы своего наименьшего значения. Стоит подумать, например, о множестве всех действительных положительных чисел: они все больше или равны нулю, но нет ни одного, которое было бы наименьшим (для любого выбранного нами числа всегда будет меньшее число). Нижней границы множества (нуля) невозможно достичь в рамках самого множества (положительных чисел), так что нет и минимума. Усилия Вейерштрасса и его математической школы, направленные на строгое обоснование существования u, разбились об этот вопрос. Однако физики продолжали считать, что так называемый принцип Дирихле гарантирует решение проблемы Дирихле. И лишь Гильберту — около 1904 года — удалось возродить принцип и доказать несомненное существование минимума. Но чтобы объяснить его доказательство, мы должны погрузиться в пограничную область вариационного исчисления, которое стремится определить, какие функции делают интеграл наименьшим.
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Проблема брахистохроны, или кривой с самым быстрым спуском, исторически была первой проблемой в развитии вариационного исчисления. Среди всех кривых, соединяющих две точки, нужно найти ту, вдоль которой частица, двигаясь под действием силы тяжести, падает за меньшее время. При рассмотрении всех возможных кривых, соединяющих точку А с точкой Ву ищется минимизирующая время падения, что может быть выражено в виде интеграла. То есть ведется поиск кривой или функции, которая делает наименьшим значение этого интеграла. Данная проблема была предложена в 1696 году Иоганном Бернулли (1667-1748) и была решена независимо Ньютоном, Лейбницем, Иоганном и Якобом Бернулли. Решением оказалась не прямая линия и не дуга окружности, а дуга кривой под названием циклоида (см. рисунок 3). Базовые понятия новой ветви анализа принадлежат Эйлеру и Лагранжу. Первый ввел название вариационное исчисление, а второй создал «метод вариации», который позволяет решить многие проблемы в рамках этой дисциплины. Основа вариационных проблем следующая: предполагается множество С любых элементов (чисел, геометрических точек, функций и так далее), которые обозначаются как м, и каждому элементу и назначается число F(u). Если С — это числовое множество, то F(u) — это функция от одной переменной; если С — это множество точек на плоскости, то F(u) — это функция от двух переменных, и так далее. Но если С — это множество функций, то F(u) — это то, что называется функционалоМу который в одной из различных функций, входящих в состав множества, может принимать значение экстремума (максимума или минимума). Чтобы решить проблему вариационного исчисления, сравнивали пробную функцию и со всеми ближайшими функциями, то есть с теми, которые получаются при легком варьировании пробной функции и (отсюда название «вариационное исчисление»), и вычисляли функционал F для каждой функции. Для функции, являющейся решением, характерно, что функционал для всех ближайших функций всегда больше (если мы ищем минимум). В этом суть «метода вариации». Эйлер и Лагранж обнаружили: для того чтобы функция и множества С предоставляла экстремальное значение (максимум или минимум) функционалу, F(ü) должно удовлетворять некоторому дифференциальному уравнению (уравнениям Эйлера — Лагранжа). Однако удовлетворение данному уравнению — необходимое, но недостаточное условие. РИС. 3:
Дуга циклоиды между А и В.
РИС. 3:
Дуга циклоиды между А и В.
 РИС. 4:
Какую из трех возможных траекторий выберет частица, чтобы из А попасть в В? Принцип наименьшего действия устанавливает, что это траектория, минимизирующая величину под названием действие.
РИС. 4:
Какую из трех возможных траекторий выберет частица, чтобы из А попасть в В? Принцип наименьшего действия устанавливает, что это траектория, минимизирующая величину под названием действие.
Мерой успеха этой плеяды идей является то, что многие математики XVIII и XIX веков стремились истолковать появлявшиеся в физике дифференциальные уравнения как экстремальные условия определенных функционалов. Законы физики можно было переписать в терминах принципов минимума, поскольку природа всегда стремится к оптимизации. Эту же цель преследовали Пьер Луи де Мопертюи (1698-1859) в механике по принципу наименьшего действия (см. рисунок 4), а также Пьер де Ферма (1601-1665) в оптике: траектория, которой следует луч света, проходя из точки А в другую точку В другой среды, — это траектория, требующая наименьшего времени. Физические трактаты конца XIX века были полны подобных принципов, утверждающих, что определенные физические процессы всегда протекают так, чтобы минимизировалось некое количество. Это были так называемые вариационные принципы. Данная уважаемая область анализа была видом продолжения анализа бесконечно малых. Если традиционный анализ показывал, как найти максимумы или минимумы функции, вариационное исчисление демонстрировало, как определить функцию, максимизирующую или минимизирующую определенный функционал, который обычно выражен в виде интеграла. Однако эта проблема оказалась намного сложнее, и в конце XIX века еще нельзя было определить ряд критериев, гарантировавших существование экстремума (максимума или минимума). Таким образом, неудивительно, что вариационное исчисление касается 3 из 23 проблем Гильберта. В то время как в проблеме 23 Гильберт задался вопросом о возможном обобщении вариационных методов, в проблемах 19 и 20 он озаботился свойствами и существованием решений проблем вариационного исчисления. Два вопроса оставались открытыми. Первый — существование или отсутствие решения (проблема 20), и второй — свойства, которым в случае своего существования это решение удовлетворяет. Если отбросить техническую оболочку, в проблеме 19 Гильберт спрашивал, должны ли физические проблемы, которые обычно позиционируются как проблемы вариационного исчисления (проблема Дирихле, например), всегда иметь решения с наилучшим поведением: всегда ли решения такие же плавные и регулярные, как аналитические функции (которые можно продифференцировать бесконечное число раз)? Эта проблема была решена в 1904 году российским математиком Сергеем Бернштейном (1880-1968) в его докторской диссертации (одним из руководителей которой был Гильберт). Бернштейн доказал, что решения уравнений в частных, интересовавших Гильберта производных (включая решения уравнения потенциала Лапласа), были, в случае их существования, регулярными, с идеальным поведением, если они удовлетворяли некоторым довольно простым условиям об их трех первых производных. Становилось очевидным, что, например, если интеграл Дирихле достигал своего минимума, то происходило это обязательно в допустимой функции. Но в том же 1904 году Гильберт удивил математический мир, восстановив доверие к принципу Дирихле, которое тот утратил после критики Вейерштрасса. До Вейерштрасса предполагалось, что в вариационном исчислении у любого функционала есть минимум. Гильберт доказал, что в конкретном случае энергии ДирихлеJ(u) действительно есть минимум. Он построил минимизирующую последовательность функций, значения которой для интеграла были каждый раз все более низкими и сходились к наименьшему значению. И на ее основе он получил минимум, то есть функцию иу которая де факто достигала этого наименьшего значения. Физики и математики могли вздохнуть с облегчением.
НАУКА НА РАСПУТЬЕ
В конце XIX века физики работали в рамках совместного опыта. Классическая механика (созданная Ньютоном) и классическая электродинамика (завершенная Максвеллом) предоставляли абсолютно удовлетворительный для понимания окружающего нас мира материал. С увеличением точности измерительных приборов и возможности осуществлять все более сложные эксперименты физики начали изучать явления в не самых привычных условиях: при очень высоких скоростях (близких к скорости света) и на макрокосмическом или микроскопическом уровне. Именно тогда стали возникать расхождения с прогнозами, которые давала классическая физика, что привело к пересмотру ее оснований и породило две великие физические теории прошлого века: теорию относительности и квантовую теорию. Первая ставила своей целью объяснить явления, происходящие при высоких скоростях (специальная теория относительности) и космических масштабах (общая теория относительности), вторая же изучала явления атомного масштаба (квантовая механика). К 1900 году ясность классической физики скрывали всего четыре тучи — проблемы, которые она не могла объяснить: излучение черного тела, фотоэлектрический эффект, спектры химических элементов и эфирный ветер. Первые три проблемы дали дорогу квантовой, а последняя — релятивистской физике. Классический принцип относительности, обязанный своим рождением Галилею, не был способен дать объяснение некоторым электромагнитным явлениям, измеряемым интерферометром (эксперимент Майкельсона — Морли). В 1905 году Альберт Эйнштейн (1879-1955) заложил основы специальной теории относительности в своей статье «К электродинамике движущихся тел». Чтобы решить мнимое противоречие, которое проявлялось при изучении поведения уравнений Максвелла в трансформациях Галилея (не прибегая к гипотетическому эфирному ветру), Эйнштейн предложил поддержать теорию Максвелла, изменив механику Ньютона. Нужно было оставить трансформации Галилея, заменив их на трансформации Лоренца, и принять революционную гипотезу: инвариантность скорости света. Среди его выводов были следующие: отказ от эфира, относительность одновременности, сжатие пространства, замедление времени и так далее. Специальная теория относительности вмиг перечеркнула иллюзию об абсолюте пространства и времени классической физики. Специальная теория относительности, хотя и была чрезвычайно дерзкой с позиции физики, не требовала математики, неизвестной на тот момент физикам и лежавшей в основе работ Пуанкаре и Хендрика Лоренца (1853-1928). В своем озарении Эйнштейн применил не очень требовательную математику. Однако некоторые физики и математики посчитали, что столь радикальные физические и философские идеи должны быть подкреплены новыми математическими формулировками. И здесь вступил в игру старый товарищ Гильберта, Герман Минковский.ГИПОТЕЗА ВАРИНГА
Как для Минковского, так и для Гильберта теория чисел была самым чудесным порождением человеческой мысли. В 1908 году, взяв перерыв в работе, чтобы поправить здоровье, Гильберт доказал гипотезу, предложенную британским математиком Эдуардом Варингом (1734-1798): «Любое целое число представимо как сумма максимум девяти кубов; любое число можно представить в виде не более 19 четвертых степеней, и так далее». Другими словами, без каких- либо доказательств утверждалось, что для любой степени к существует некоторое минимальное число таких степеней (назовем его g(k), поскольку оно зависит от степени выбранного к), которое позволяет выразить любое число л в виде суммы ровно g(k) к-х степеней: n =х1k + х2k + ... + xg(k)k. В 1770 году Жозеф-Луи Лагранж доказал, что любое число — это сумма четырех квадратов, то есть что g(2) = 4. Но до Гильберта прогресса в этом вопросе не наблюдалось. Для некоторых конкретных значений k(k = 3, 4, 5, 6, 7 и 8) удалось ограничить значение g(k); так доказали, что g(4)≤53, но было еще далеко до доказательства, что для записи любого числа достаточно всего 19 четвертых степеней, то есть что g(4) = 19. Эдуард Варинг.
Эдуард Варинг.
Заслуженная премия
Гильберт напрямую не оценивал значения g(k) (это было сделано в XX веке) и косвенно доказал, что функция g(k) четко определена, то есть для каждого к она принимает конечное значение (никогда не принимает бесконечных значений, из чего можно сделать вывод: всегда существует минимальное число степеней, необходимых для записи любого числа). Это достижение принесло ему в 1910 году премию Яноша Бойяи. Как член жюри Пуанкаре отдал должное работе немецкого математика не только потому, что она относилась к теории чисел, но и за широкий спектр затронутых в ней тем: инварианты, аксиоматические основания геометрии, принцип Дирихле и так далее. Он также оценил строгость и простоту примененных методов, в которых проявился талант Гильберта как преподавателя.Друзья снова встретились в 1902 году. Гильберт отказался от кафедры в Берлине, чтобы остаться в Гёттингене, но добился должности для своего дорогого коллеги. Гёттинген в одночасье превратился в Мекку для математиков. Здесь жили сразу три пророка — Клейн, Гильберт и Минковский. С 1902 по 1909 год последние двое вместе читали несколько курсов по математической физике, в частности по электродинамике движущихся тел (сегодня известной как теория относительности). Минковский очень внимательно отнесся к пререлятивистским теориям Пуанкаре и Лоренца и сразу же откликнулся на подход Эйнштейна. Его очень удивило, что этот революционный подход принадлежит его бывшему ученику в Цюрихе, в математических знаниях которого он несколько сомневался. Минковский рассматривал время как четвертое измерение. Между пространством и временем есть нерушимая связь, они формируют единое целое — пространство-время. Все, что у Эйнштейна казалось туманным, в псевдоевклидовом четырехмерном мире, который вообразил Минковский, становилось ясным. Это геометрическое обрамление способствовало распространению специальной теории относительности. Его воздействие было очень сильным, хотя его приняли не сразу (настораживал тот факт, что чтобы оперировать физическими понятиями, требовалось обращаться к геометрии с ее отрицательными векторами). Эйнштейну это показалось поверхностной эрудицией, и в ответ Гильберт возразил: «Любой мальчик на улицах Гёттингена понимает в четырехмерной геометрии больше, чем Эйнштейн». Минковский изложил свою позицию в нескольких лекциях 1908 года, но не дождался их публикации и не успел насладиться успехом: в 1909 году ученый умер в результате осложнений после операции по удалению аппендикса. Эта потеря усилила депрессию, в которой Гильберт находился из-за нервного истощения.
ЭЙНШТЕЙН, ГИЛЬБЕРТ И УРАВНЕНИЯ ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
С 1911 года Эйнштейн направлял усилия на то, чтобы включить гравитацию в свою специальную теорию относительности. Он искал общую теорию. Несмотря на природное упрямство, Эйнштейнпризнал пользу выкладок Минковского, ведь они навели его на мысль, что ключ находится в геометрии. То есть чтобы представить эффекты гравитации посредством геометрической структуры пространства-времени, объекты должны располагаться в предусмотренном виде. Нужно было геометризовать гравитацию. Как простыня, которую держат два человека, деформируется, когда на нее падает какой-то предмет, так и тело с огромной массой, как Земля, искривляет пространство- время вокруг него, и эта кривизна является причиной движений гравитационного притяжения, которое мы ощущаем на его поверхности.
Как простыня, которую держат два человека, деформируется, когда на нее падает какой-то предмет, так и тело с огромной массой, как Земля, искривляет пространство- время вокруг него, и эта кривизна является причиной движений гравитационного притяжения, которое мы ощущаем на его поверхности.
В первых попытках математические выкладки Эйнштейна были довольно примитивными, и результаты их были незначительными. Если геометрия пространства-времени должна была зависеть от ее энергетико-материального содержания, то есть если гравитация должна была искривлять пространство-время, требовалась изменчивая геометрия, не заданная изначально и существенно отличающаяся от обычной. Знакомый математик указал Эйнштейну на классические работы Гаусса, Римана и в особенности на публикации Грегорио Риччи (1853-1925) и Туллио Леви-Чивита (1873-1941) в 1901 году. Последние содержали большую часть элементов геометрии Римана, необходимых для общей теории относительности. Вместе со своим другом Марселем Гроссманом (1878-1936) Эйнштейн начал изучать эти работы и обнаружил, что в них содержится необходимый ему математический аппарат, о котором он раньше не подозревал. В конце 1913 года физик и математик совместно опубликовали 28-страничную брошюру «Набросок обобщенной теории относительности и теории гравитации». Их целью было смоделировать Вселенную как геометрическую четырехмерную разновидность, снабженную римановой метрикой, или расстоянием, заданным тензором: 4 ds2= Σ gijdxidxj. i,J=1 Этот метрический тензор, который определял геометрические свойства (естественно, неевклидовы), характеризовал также гравитационное поле (см. рисунок на предыдущей странице). Однако уравнения гравитационного поля, содержащиеся в статье, не были верны, и вскоре от них отказались. Тогда для Эйнштейна начался долгий и утомительный период, прежде чем к концу ноября 1915 года он начал различать свет истины. Эйнштейн боролся с тензорным исчислением, чтобы получить правильные уравнения. Он внедрялся в область, куда осмелились ступить лишь некоторые математики. Одним из них был наш герой, Давид Гильберт. С 1909-го и практически до 1920 года Гильберт демонстрировал большую склонность к теоретической физике, применяя к ней методы вариационного исчисления. Итогом этих лет стала книга, написанная в 1924 году в соавторстве с Рихардом Курантом. Учебник «Методы математической физики» в течение десятилетий пользовался огромным успехом. Гильберт направил свое внимание на насущные физические проблемы — атома и теории относительности. Благодаря поддержке Пауля Вольскеля, богатого немецкого промышленника, увлекавшегося математикой, Гильберт периодически организовывал в Гёттингене исключительные лекции и принимал знаменитых академиков из других стран (он шутил, что единственная причина, по которой он все еще не доказал последнюю теорему Ферма, состоит в задаче не получить 100 000 марок, назначенных за доказательство премии, и не сразить одним ударом курицу, несущую золотые яйца). Среди первых гостей были Пуанкаре и Лоренц, прочитавшие лекции по вопросам, связанным с релятивистской механикой. Но, пожалуй, самым нашумевшим событием стал приезд Эйнштейна в начале лета 1915 года. Это была их первая встреча. Эйнштейн читал цикл из шести лекций в Гёттингене и остановился в доме Гильбертов. Проведя несколько дней в его компании, Гильберт загорелся поставить свои математические способности на службу новым идеям гравитации. В течение последующих месяцев они оба лихорадочно работали, часто обмениваясь письмами. Они преследовали одну и ту же цель: найти уравнения общей теории относительности. В какой-то момент Эйнштейна обеспокоила столь пылкая вовлеченность Гильберта в этот процесс, и когда в конце ноября 1915 года Гильберт предложил в письме Эйнштейну свои уравнения, тот, недавно нашедший итоговые уравнения общей теории относительности, сразу же обозначил собственное первенство. Гильберту оставалось только послать письмо с поздравлением.
УРАВНЕНИЯ ПОЛЯ В ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Пространство-время Минковского четырехмерное. Материя искривляет его так, что объекты перестают двигаться по прямым линиям и начинают двигаться по кривым, по геодезическим, под действием гравитации или некоторого ускорения. Чем больше массы или энергии мы введем, тем больше искривится пространство-время Минковского. Отношение между присутствием массы-энергии и формы четырехмерного пространства-времени задано уравнениями поля Эйнштейна: Gμν = (8πG)/(c4·Tμν). В левой части уравнения появляется Gμν, то есть тензор кривизны Эйнштейна: он измеряет деформацию пространства и зависит, в свою очередь, от метрического тензора, от gij. расстояния. В правой части, кроме числа π, постоянной всемирного тяготения G и скорости света с, появляется тензор энергия-импульс Τμν, который воплощает материю. Подводя итог: пространство диктует материи, как она должна двигаться, а материя обозначает для пространства, как оно должно искривляться. Отметим, что в 1917 году Гильберту удалось доказать: евклидова геометрия является настоящей геометрией Вселенной только тогда, когда тензор энергия-импульс точно равен нулю, то есть при отсутствии материи. В любом случае то, что евклидова геометрия была сброшена с пьедестала в глобальном отношении, ни в коем случае не означает, что она не несет локальной пользы в нашем окружении.Считалось, что Гильберт вывел уравнения теории относительности гравитационного поля раньше, чем Эйнштейн, хотя он никогда не оспаривал его первенство. Гильберт отправил свою статью в печать 20 ноября 1915 года, за пять дней до Эйнштейна. Воспользовавшись своими обширными математическими знаниями, он сформулировал вариационный принцип, из которого выводились уравнения гравитации и электромагнетизма (Эйнштейн, наоборот, ограничился гравитационным взаимодействием.) Он утверждал, что законы физики определяются тем, что некоторый интеграл достигает своего минимума. С другой стороны, некоторая функция, зависящая от римановой метрики, остается инвариантной к произвольным трансформациям координат. С гравитацией и электромагнетизмом он хотел сделать то же самое, что уже было сделано для геометрии: четко установить основания и вывести результаты из минимального числа аксиом или базовых принципов. Аксиоматическая структура, дедуктивный метод и вариационное исчисление — это три основных составляющих вклада Гильберта в физику. Но если статья Гильберта содержала уравнения общей теории относительности в виде, где была геометризована не только гравитация, но и электромагнетизм, и была отправлена в печать на пять дней раньше, чем статья Эйнштейна, разве не означает это, что честь открытия общей теории относительности принадлежит Гильберту, пусть даже Эйнштейн подготовил ему почву? Ответ на этот вопрос отрицательный по двум причинам. Первая: теория Гильберта не идентична теории Эйнштейна. Формально они равносильны, но различались по физической интерпретации. Для Эйнштейна аксиоматический метод не имел большой пользы в материи; кроме того, в отличие от большинства своих коллег, он не был сторонником идеи, что любая физическая теория должна быть выражена через вариационный принцип. Хотя сегодня имя Эйнштейна ассоциируется у нас с физиком-теоретиком, зацикленным на крайне абстрактных вопросах, следует понимать, что как в годы учебы, так и в период творческого расцвета он всегда был очень близок к экспериментальной реальности. Ему была в большей степени свойственна индукция, чем дедукция.
НАУКА И ВОЙНА
В 1914 году большая часть европейцев в эйфории приветствовала начало Первой мировой войны. Гильберт, наоборот, с первых дней не скрывал, что война кажется ему абсурдной. В августе этого года 93 знаменитых немецких интеллектуала направили манифест «К цивилизованному миру» в ответ на возрастающее возмущение действиями немецкой армии. Под влиянием националистической пропаганды Феликс Клейн подписал это обращение, поддерживающее политику кайзера. Попросили его подписать и Гильберта, но тот отказался, объясняя это тем, что не знает наверняка, являются обвинения в адрес немецких войск ложными или нет. Эта позиция сблизила его с пацифистом Эйнштейном, который тоже отказался подписывать манифест. В разгар войны, в 1917 году, Гильберт опубликовал некролог Жану Гастону Дарбу(1842-1917), выдающемуся французскому математику, в котором превозносил этого ученого. Когда студенты окружили его дом, требуя переписать заметку, Гильберт потребовал у них извинений (и получил их). В результате европейские коллеги увидели в нем человека свободного духом, презирающего традиции и условности. Так что по окончании войны, когда Германия была разгромлена, его репутация сохранилась, и на первом международном конгрессе математиков, состоявшемся в межвоенный период (Болонья, 1928, VIII Международный конгресс математиков), он не колеблясь настаивал на универсальном характере математики, поскольку любые границы — это против природы. Жан Гастон Дарбу.
Жан Гастон Дарбу.
Вторая причина, более важная, состоит в том, что, как недавно выяснил историк математики Лео Корри, содержание статьи, представленной Гильбертом в Академию наук 20 ноября, не совпадает с опубликованным. Гильберт внес исправления 6 декабря с учетом представленного Эйнштейном 25 ноября. Похоже, Гильберт изменил свои уравнения, чтобы приспособить их к уравнениям Эйнштейна. Так что этот небольшой спор не вылился в долгосрочную вражду. У нас произошла размолвка, причины которой я не хочу анализировать. [...] Просто стыдно подумать, что двое приличных людей, сумевших отчасти отрешиться от мелких страстей человечества, не могут наслаждаться общением друг с другом. Альберт Эйнштейн в письме Гильберту от 20 декабря 1915 года
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Если исследовательский этап Гильберта в области вариационного исчисления привел его к разработке общей теории относительности, то период между 1904 и 1910 годами, который он посвятил интегральным уравнениям, позволил ему сделать то же с квантовой механикой. Речь, конечно же, о самом важном вкладе Гильберта в математический анализ и опосредованно в физику, о ряде статей, которые позже он объединил в монографии «Основания общей теории линейных интегральных уравнений» (1912), содержащей не только строгую математическую теорию, но и множество разнообразных физических применений — от кинетической теории газов до теории излучения. Но начнем сначала. Для интегрального уравнения характерно, что неизвестная функция также появляется внутри интеграла. Например: b x(t) + ∫K(t,s)x(s)ds = ƒ(t), a где функция K(t, s) является ядром интегрального уравнения. При заданном ядре K(t, s) и функции ƒ(t) (непрерывные функции) требуется найти неизвестную функцию x(t). В XIX веке было сформулировано несколько интегральных уравнений по физическим вопросам, таким как проблема брахистохроны или проблема Дирихле. Но только в 1888 году Поль де Буа-Реймон (1831 — 1889) ввел термин «интегральные уравнения» для их обозначения и заявил о необходимости разработать общую теорию этих уравнений в качестве альтернативного метода решения задач с дифференциальными уравнениями. В 1900 году шведский математик Ивар Фредгольм (1866- 1927) позаимствовал внешне безобидное замечание итальянского математика Вито Вольтерры (1860-1940) и предложил новый способ решения проблемы Дирихле с использованием интегральных уравнений. Изучив уравнения потенциала, или уравнения Лапласа с граничными условиями, Фредгольм трансформировал проблему в интегральное уравнение, как приведенное выше, и воспользовался схожестью этого интегрального уравнения и системы бесконечных линейных уравнений, когда интеграл заменяется суммами Римана. Интеграл — это процесс вычисления площади, ограниченной кривой. Сумма Римана — по сути, всего лишь равносильный способ вычисления значения интеграла: проводится конечное число прямоугольников внутри площади, ограниченной кривой, и эта площадь приближается к сумме площадей каждого из этих прямоугольников (см. рисунок). Когда число прямоугольников стремится к бесконечности, суммы Римана сходятся в точном значении интеграла. В этой технике интегральное уравнение разрастается в систему бесконечных линейных уравнений. Следовательно, решить отправное интегральное уравнение — значит решить всю систему бесконечных линейных уравнений. Сумма Римана — это сумма площадей прямоугольников на рисунке, которая служит для приближения к площади, ограниченной кривой, то есть к интегралу функции ƒ(x) от a до b.
Сумма Римана — это сумма площадей прямоугольников на рисунке, которая служит для приближения к площади, ограниченной кривой, то есть к интегралу функции ƒ(x) от a до b.
Сенсационные результаты Фредгольма распространились со скоростью звука. Зимой 1900-1901 года гостивший в Гёттингене преподаватель провел аналогию между интегральными уравнениями и системами линейных уравнений на семинаре Гильберта, и тот живо заинтересовался данной темой и направил на нее всю свою производительность (в пылу он даже предсказал, что новый инструмент позволит в итоге доказать гипотезу Римана). Шесть работ на эту тему, опубликованные им между 1904 и 1910 годами, содержали зачатки нового ответвления анализа (функциональный анализ) и привели к понятию гильбертова пространства, основанию всей квантовой механики.
И СВЕРШИЛСЯ ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ!
Функциональный анализ изучает функции в совокупности, то есть пространства функций. Наиболее явные его истоки находятся в интегральных уравнениях, которые определяют алгебраизацию анализа (типичный подход функционального анализа), но также присутствуют в вариационном исчислении, где впервые появляются идеи множества функций, допустимых для решения проблемы и расстояния между функциями (через функционал). Математический аппарат, утвердившийся с функциональным анализом, в конце 1920-х годов обратился в столп целой физической дисциплины — квантовой механики. Благодаря этому ключевому факту его мощные формулировки, связанные с распространением квантовых выкладок, постоянно обновлялись. Функциональный анализ обобщает геометрические понятия w-мерного пространства (расстояние, теорема Пифагора и другие) до функциональных пространств бесконечной размерности. Среди этих пространств бесконечной размерности выделяется так называемое гильбертово пространство, построенное в области интегральных уравнений самим Гильбертом, но аксиоматизированное в связи с квантовой механикой его талантливым учеником Джоном фон Нейманом, который назвал пространство именем своего учителя около 1930 года. Гильбертово пространство в зачаточном виде появляется в статье 1906 года (четвертой из шести статей об интегральных уравнениях и первой настоящей статье о функциональном анализе). Можно сказать, что гильбертово пространство образуют функции, являющиеся решением интегральных уравнений. Когда Гильберт изучал интегральное уравнение, ему в голову пришла идея рассмотреть особую систему функций, которая выполняла бы некоторые свойства (для тригонометрической системы — быть базисом функционального пространства) и свести решение уравнения к определению коэффициентов неизвестной функции относительно этой системы (точнее, координат неизвестной функции относительно этого базиса пространства). Рассматривая тригонометрическую систему, он старался найти неизвестную функцию, представив ее с помощью коэффициентов Фурье (бесконечной последовательности чисел, позволяющих выражать функцию интегрируемого квадрата в виде суммы тригонометрических функций, умноженных на эти числа). Коэффициенты, как он заметил, удовлетворяли условию конечности суммы их квадратов. После подстановки этих отождествлений (или разработок) в интегральное уравнение проблема преобразилась в проблему решения бесконечного числа линейных уравнений с бесконечными неизвестными (коэффициентами функций из суммируемого квадрата). Продолжая данный пример, если в уравнении b x(t) + ∫K(t,s)x(s)ds = ƒ(t), a представить функции x(t), ƒ(t) и K(t, s) их коэффициентами Фурье, то это уравнение записывается как бесконечная система уравнений: ∞ xp + ∑kpqxq = ƒp p = 1, 2, 3... g=1 при условии, что сумма различных коэффициентов в квадрате конечна, то есть ∞ ∑x2p < ∞. p=1 Таким образом, при переходе из царства непрерывного в царство дискретного интеграл преобразуется в сумму (аналогичную операцию). Пространство всех последовательностей действительных чисел суммируемого квадрата (сегодня обозначаемое l2), где нужно искать решение, — это и есть гильбертово пространство. В этом пространстве числовых последовательностей, по аналогии с обычным евклидовым пространством, Гильберт определил расстояние и распространил на него классические понятия предела, непрерывности и так далее. Как Гильберт, так и его лучшие ученики (в особенности Эрхард Шмидт) досконально исследовали это геометрическое сходство функционального пространства l2 с обычным геометрическим пространством R". Вся теория о гильбертовых пространствах способствовала выходу на сцену первого известного пространства с бесконечным числом измерений в его каноническом представлении об l2. Эти годы были решающими, прежде чем появилась возможность общего анализа пространств функций. В 1906 году увидела свет докторская диссертация Мориса Фреше (1878— 1973), которая имела огромное влияние, поскольку в ней в абстрактном виде было введено понятие расстояния во множестве функций, а также остальные связанные геометрические понятия. Через некоторое время, в 1907 году, два молодых математика — бывший ученик Минковского Эрнст Фишер (1875-1954) и Фридьеш Рис (1880-1956), в ту пору учитель средней школы из венгерского городка, — независимо друг от друга открыли неожиданную связь между расцветающим функциональным анализом и другим великим математическим открытием того времени — теорией интегрирования Анри Лебега (1875-1941), которая была призвана залатать прорехи классических теорий интегрирования Коши и Римана. Теорема Фишера — Риса гласит, что существует соответствие, или изоморфизм, между пространством Гильберта l2 и пространством функций интегрируемого квадрата (которое сегодня мы называем L2). В одночасье родилась вторая модель гильбертова пространства. Эти работы позволили ввести новые функциональные пространства, такие как обобщение уже известных: пространств lр и Lp при р > 1 (например, если р = 3, пространство последовательностей/функций суммируемого/интегрируемого куба, и так далее). Групповой портрет. Слева направо: Альфред Хаар, сын Гильберта Франц, его неразлучный друг Герман Минковский, неизвестная женщина, Кёте Г ильберт, Давид Гильберт и Эрнст Хеллингер.
Групповой портрет. Слева направо: Альфред Хаар, сын Гильберта Франц, его неразлучный друг Герман Минковский, неизвестная женщина, Кёте Г ильберт, Давид Гильберт и Эрнст Хеллингер.
 Эйнштейн в гостях у Лоренца в Лондоне в 1921 году. Для установления теории относительности немецкий физик воспользовался работой Лоренца и Пуанкаре, а также математической помощью Г ильберта.
Эйнштейн в гостях у Лоренца в Лондоне в 1921 году. Для установления теории относительности немецкий физик воспользовался работой Лоренца и Пуанкаре, а также математической помощью Г ильберта.
 Джон фон Нейман, ученик Гильберта, который дал имя своего учителя гильбертову пространству.
Джон фон Нейман, ученик Гильберта, который дал имя своего учителя гильбертову пространству.
Официально функциональный анализ был введен в 1922 году, когда вышла из печати книга «Лекции по функциональному анализу» Поля Леви (1886-1971). В том же году была опубликована докторская диссертация поляка Стефана Банаха (1892-1945), в которой тот стремился доказать ряд теорем, справедливых для различных функциональных пространств, не останавливаясь на конкретной природе этих пространств (на конкретных функциях, которые входят в их состав). Любопытно, что многие открытия Банаха в области функционального анализа были сделаны в шуме «Шотландского кафе» во Львове (в то время считавшемся территорией Польши), где он нацарапывал заметки на мраморной крышке стола или на салфетке. Результатом этих заметок Банаха и других известных математиков, его компаньонов, стала «Шотландская книга» — один из самых важных математических документов XX века.
КВАНТЫ, МАТРИЦЫ И ВОЛНЫ
После тысячи и одной неудачной попытки объяснить излучения черного тела (то есть тела, находящегося в закрытой полости) немецкому физику Максу Планку (1858-1947) наконец это удалось. Он заявил, что излучение и поглощение энергии всегда происходит пучками, в прерывистом, или «квантизованном», виде. Энергия, как и деньги, не принимает значения внутри непрерывного диапазона, а только в дискретных единицах. «Дискретизация», объявленная Планком, была настоящим актом отчаяния. Рождение квантовой теории относится к 14 декабря 1900 года, когда его закон об излучении черного тела был представлен публично. Но в числе действующих лиц старой квантовой теории, кроме Планка, присутствуют Альберт Эйнштейн и Нильс Бор (1885-1962). В 1905 году, ставшем чудесным годом, Эйнштейн применил квантовую гипотезу к изучению света: световые волны состоят из мельчайших частиц (которые позже получили название фотонов), как это видно из фотоэлектрического эффекта. До середины XIX века корпускулярное видение материи, наследство Ньютона, доминировало над волновым видением. До 1900 года существовала гибридная концепция: твердые тела и флюиды (жидкости и газы) считались состоящими из частиц, а электромагнитное излучение понималось как волны. Теперь же выяснилось, что физикам нужно отказаться от классической концепции материи (волна или частица) ради новой концепции: волна и частица (как в случае со светом). В 1913 году Бор, стипендиат (благодаря поддержке фонда пивоваренной компании) лаборатории Эрнеста Резерфорда (1871-1937), квантизовал атом с целью объяснить атомные спектры. Прерывистые линии спектров были следствием квантизации энергии электронов внутри атома. К несчастью, модель атома Бора потерпела крах при применении ее к многоэлектронным атомам, и ученые постепенно приходили к выводу, что необходимо радикальное изменение в основаниях физики: появление нового вида механики (Макс Борн (1882-1970) назвал ее квантовой), который содержал бы связную аксиоматику, независимую от классических теорий, и преодолел бы мешанину из принципов, законов и вычислительных инструкций, составлявших старую квантовую теорию.У Зоммерфельда я научился оптимизму, у гёттингенцев — математике, а у Бора — физике. Вернер Гейзенберг
В 1925 году молодой физик Вернер Гейзенберг (1901-1976), приват-доцент в университете Геттингена, вывел основы квантовой механики, выздоравливая после приступа сенной лихорадки на острове Гельголанд. Гейзенберг настаивал, что множество всех частот и амплитуд излучения, испускаемого атомом, может считаться полным описанием системы атома, даже если невозможно истолковать его в смысле электронной траектории, которая вызывает излучение, поскольку орбиты электронов внутри атома ненаблюдаемы.
ОДНА ПРОБЛЕМА, ДВА РЕШЕНИЯ
Посмотрим, как квантовые механики решали проблему нахождения различных энергетических уровней электрона атома водорода. В матричной механике нужно было «диагонализовать» матрицу Гамильтона Н, измеряющую общую энергию системы, то есть определить матрицу S так, чтобы матрица W = S-1HS была диагональной; так диагональные элементы Еn — это энергетические значения электрона:
В свою очередь, в волновой механике требовалось решить волновое уравнение Шрёдингера, то есть следующее уравнение в частных производных: -Δψ + Vψ = Εψ, где ψ — волновая функция (независимая от времени), V — потенциал, а Е — энергия. Если определить оператор Гамильтона как Η = -Δ + V (то есть кинетическая энергия плюс потенциальная энергия), предыдущее уравнение можно переписать, чтобы оно приняло вид Ηψ = Εψ и представляло собой то, что известно как проблема собственных значений, или проблема Штурма — Лиувилля, поскольку ею занимались французские математики Жак Шарль Франсуа Штурм (1803-1855) и Жозеф Лиувилль (1809-1882). Она называется так, поскольку это последнее уравнение допускает решение для некоторых значений ψ и Е, которые получают название собственных функций и собственных значений, соответственно.
Собственные значения
В классической физике собственные значения определяли, например, характерные частоты колебания упругой мембраны, так что любое колебание могло выражаться как наложение этих базовых видов колебания. В квантовой физике собственные значения Еп — это как раз возможные уровни энергии электрона атома водорода. Разницы между этими собственными значениями дают частоты испускаемых квантов света (фотонов), описывая таким образом структуру спектра излучения атома. В свою очередь, различные состояния электрона заданы собственными функциями ψn, соотносящимися с собственными значениями. В математике множество собственных значений Еn матрицы или оператора называется спектром. В результате чудесного совпадения математический спектр (название для которого Гильберт выбрал случайно) в итоге стал ключевым для объяснения физических спектров атомов. Ученый говорил: «Я разработал теорию о бесконечных переменных и даже назвал ее спектральным анализом, совсем не предполагая, что позже она найдет применение для настоящего физического спектра». Это была счастливая случайность. Жак Шарль Франсуа Штурм
Жак Шарль Франсуа Штурм
 Жозеф Лиувилль.
Жозеф Лиувилль.
Кроме того, он выяснил, что эти множества чисел (соответствующие коэффициентам Фурье классического выражения движения электрона) не коммутируют. Другими словами, в отличие от классических величин, квантовые в целом выполняют QP ≠ PQ. Через несколько месяцев двое коллег из Геттингена, физик Макс Борн и математик Паскуаль Йордан (1902-1980), признали, что эти множества чисел Q и Р ведут себя как математические матрицы (хотя сам Гейзенберг, по его словам, даже не знал, что такое матрица). Матричная квантовая механика выросла в саду, возделанном Гильбертом. Однако Геттинген разделился на две группы: Гильберт и его сторонники верили в большой успех, обусловленный введением матричного исчисления в физику, а их противники отмахивались от утомительной метаматематики, наполнившей атомную физику. В рождественские каникулы 1925-1926 года Эрвин Шрё- дингер (1887-1961) осветил волновую квантовую механику, пока наслаждался обществом своей последней возлюбленной (по словам Германа Вейля, его коллеги по Цюриху). В отличие от юных физиков и математиков Геттингена, но как представителю значительной части старой гвардии, Шрёдингеру не очень импонировала квантовая механика Гейзенберга, Борна и Йордана. В поисках интуитивно более понятной теории, в которой бы применялись только классические математические инструменты, он вывел свое знаменитое волновое уравнение. Идея возникла при изучении движения электрона, как если бы речь шла о волновом движении, волновая функция Ψ которого отвечала бы за описание состояния системы. Его работа была принята с воодушевлением, потому что решить дифференциальное уравнение — чем физики занимались уже несколько веков — казалось намного проще, чем найти решение некоторых матричных уравнений. Итак, панорама, которая была представлена физикам в начале весны 1926 года, не могла быть более парадоксальной: в их распоряжении имелись две механики, которые объясняли и прогнозировали одни и те же явления, несмотря на то что в каждой использовался абсолютно разный подход и намечалась абсолютно разная концепция микрокосмоса. Если Шрёдингер называл матричную механику «противоестественной», то Гейзенберг не сдавался и окрестил волновую механику «отталкивающей». Некоторые физики — сам Шрёдингер, Карл Эккарт (1902-1973) и Вольфганг Паули (1900-1958) — стремились прояснить формальные отношения между обеими механиками. Они пришли к выводу, что оба механизма математически эквивалентны, хотя их доказательство того, что можно построить матрицы Q и Р на основе волновых функций Ψ и наоборот, было не совсем корректным. В признании сходства между двумя механизмами есть заслуга Гильберта. Он посмеивался над Борном и Гейзенбергом, так как, открыв матричную механику, они столкнулись с теми же трудностями, с которыми, конечно же, сталкиваются все математики, работающие с бесконечными матрицами. Когда они обратились за помощью к Гильберту, он сказал им (вспомнив свою работу над интегральными уравнениями 20-летней давности), что единственный раз он столкнулся с матрицами, когда те появлялись как побочный продукт изучения собственных значений дифференциального уравнения с граничными условиями (то есть когда интегральное уравнение преобразовывалось в систему бесконечных линейных уравнений). Он предположил, что если они найдут дифференциальное уравнение, порождающее эти матрицы, то, возможно, получат больше информации. Гейзенберг и Борн подумали, что он сказал это для того, чтобы отвязаться от них, а на самом деле не знал решения этого вопроса. Позже Гильберт шутил, указывая на то, что если бы они его тогда послушали, то открыли бы волновую механику Шрёдингера на полгода раньше него. Это был путь, по которому шли Шрёдингер, Эккарт и Паули, чтобы показать идентичность обеих теорий с математической точки зрения.
Единственная цель теоретической физики состоит в вычислении результатов, которые могут быть сравнены с опытом, и вовсе нет необходимости в утвердительном описании всего хода явлений. Поль Дирак
Осенью 1926 года Паскуаль Йордан и британский физик Поль Адриен Морис Дирак (1902-1984) независимо друг от друга начали разрабатывать теорию преобразований, чтобы раз и навсегда объединить квантовые механики. Так как квантовые величины, введенные Гейзенбергом, определяли новый тип алгебры (для него умножение не было коммутативным), Дирак решил назвать q-числами величины, которые так себя ведут (хотя q здесь происходило не от слова quantum, а от английского queer, то есть «странный», «необычный»). Итак, абстрактная алгебра #-чисел допускает различные представления или образы (так же как одна и та же система аксиом может допускать разные модели), два из которых — матричная и волновая механика.
ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
В матричной механике речь шла о поиске матрицы S, чтобы матрица W = S-1HS была диагональной. Если выделить HS в этом уравнении, получается HS = SW. И если, применяя правило умножения матриц, записать то, что означает это последнее уравнение для элементов каждой матрицы, можно получить систему бесконечных линейных уравнений (напоминает получившуюся при преобразовании интегрального уравнения): ∞ ∑hpqSqn = EnSpn. [1] q=1 С другой стороны, в волновой механике пытались решить волновое уравнение Шрёдингера Ηψ = Εψ, определяя собственные значения, являющиеся решением. Если в уравнение ввести собственную функцию ψn, назначенную собственному значению Еn , получается: Ηψn = Εnψn. [2] Как Гильберт, так и Дирак, переформулировав обе проблемы в таком виде, перешли к их сравнению и заметили, что [1] и [2] представляют собой схожую структуру: Гамильтониан x ΧΥΖ = Энергия x ΧΥΖ. Следовательно, вопрос, которым они задались, звучал так: какие условия следует допустить, чтобы приравнять член к члену уравнения [1] матричной механики к уравнению [2] волновой механики? Так как «интегрирование» в царстве непрерывного — это аналог «сложения» в царстве дискретного (символ ∫ происходит от последовательной деформации прописной S), они решили: то, что должно заменить (при переходе от дискретного к непрерывному) первый член в [1], будет выглядеть как ∫h(х,у)ψn(у)d(у). Значит, объединение между обеими квантовыми механиками было бы достигнуто, если бы последнее выражение совпадало с первым членом в [2] в виде: Ηψn(x) =∫h(x,у)ψn(у)dy, то есть если бы любой оператор Гамильтона мог быть записан как интегральный оператор. Но это было невозможно даже для такого простого оператора, как тождество (определяемое как Ηψ = ψ для любой волновой функции). Дирак не спасовал перед трудностями и, чтобы преодолеть их, прибегнул к функции δ. Эта своеобразная функция определена δ(z)=0 для любого z≠0[3] и, как ни парадоксально, ∫δ(z)dz= 1 [4]. Как представить себе функцию, которая равна 0 во всех точках, кроме одной, и интегрирует 1? Итак, приняв эту функцию и рассматривая h(x,y)=δ(x-y) как ядро вышеприведенного интегрального уравнения, можно выразить тождество, например, как интегральный оператор, просто применив магические свойства δ: [3] [4] Ηψ(x)=∫h(х,у)ψ(у)dy=∫δ(х-у)ψ(у)dy= ψ(x)∫δ(x-y)dy=ψ(x)·1=ψ(x). С помощью подобных вычислений можно доказать, что любой оператор может быть представлен как интегральный оператор, так что обе квантовые механики оказываются принудительно унифицированными. Схематическая диаграмма дельты Дирака: «функция», которая равна 0 во всех своих точках, кроме начала, где она равна бесконечности, чтобы таким образом интегрировать 1.
Схематическая диаграмма дельты Дирака: «функция», которая равна 0 во всех своих точках, кроме начала, где она равна бесконечности, чтобы таким образом интегрировать 1.
Для того чтобы все преобразования между представлениями квантовой механики работали корректно, Дирак был вынужден прибегнуть к использованию вымышленной математической сущности — дельта-функции, которая на самом деле функцией не была. Для физиков это стало полезной идеализацией, привести которую к строгому виду должны были математики. Для математиков, наоборот, это понятие оказалось подозрительным и не обладающим математической реальностью, его использование оправдывалось только физическими применениями. Дельта-функцию Дирака ждала печальная участь, поскольку лишь в 1950 году она нашла свое место в рамках теории распределений, созданной Лораном Шварцем (1915-2002). До этого из-за отсутствия у нее строгости она оставляла равнодушными математиков Гёттингена. И именно тогда в Гёттинген приехал молодой Джон фон Нейман, чтобы поработать в качестве помощника Гильберта. Блестяще защитив докторскую диссертацию по теории множеств, он начал читать лекции по функциональному анализу вместе с Эрхардом Шмидтом в Берлине. В то время Гильберт пытался найти рациональную математическую модель для квантовой механики; но его аксиоматический подход развивался медленно, потому что ученый страдал злокачественной анемией (смертельным заболеванием, от которого он исцелился благодаря нетрадиционным методам). В 1926-1927 году Гильберт попросил своего ассистента по физике Лотара Нордгейма разложить для него по полочкам суть последних исследований, чтобы иметь возможность читать курс квантовой механики, применяя свой любимый аксиоматический метод. Фон Нейман вдохнул жизнь в проект. Под предводительством Гильберта они втроем ринулись искать строгое математическое оформление. Так, в 1927 году они вместе написали статью «Об основаниях квантовой механики». Гильберт хотел заставить работать интегральную формулировку физических проблем, более практичную, чем дифференциальный вариант, выраженный посредством волнового уравнения или дискретной версии в матричных терминах. Так же как и венгерский физик Корнелий Ланцош (1893-1974) в 1926 году (что любопытно, за месяц до того, как Шрёдингер опубликовал свое знаменитое уравнение), Гильберт, Нордгейм и фон Нейман разработали квантовую механику, пользуясь интегральными уравнениями. Однако результат этого первого приближения не был удовлетворительным, поскольку они не смогли избежать тупика дельты Дирака, чтобы перейти от одной формулировки к другой. Фон Нейман закончил работу по аксиоматическому обоснованию квантовой механики в одиночку. Он сделал это в период с 1928 по 1932 год, опубликовав серию из пяти статей и монументальный трактат «Математические обоснования квантовой механики». Чтобы придать прочную математическую основу квантовой теории, он отказался от использования дельта-функций Дирака и от предпочтения интегральных уравнений Гильберта. У него было другое оружие: функциональный анализ. Он создал абстрактное аксиоматическое обрамление, гильбертово пространство, которое включало в себя частные матричный и волновой случаи.
«ОСНАЩЕННЫЕ» ГИЛЬБЕРТОВЫ ПРОСТРАНСТВА
Квантовая механика фон Неймана, безупречная для математиков, столкнулась с тем, что физики предпочитали квантовую механику Дирака, которая оказалась более полезной, несмотря на отсутствие строгости. Благодаря работам Лорана Шварца и Александра Гротендика по функциональному анализу, в 1950-1960 годы дельта-функции приобрели статус математической природы, формализовавшись как обобщенные функции, или распределения. Так формализм Дирака перестал быть математически подозрительным, поскольку вошел в состав «оснащенных»гильбертовых пространств (или триплетов Гельфанда). Идея состоит в том, чтобы связать лучшее в формализме фон Неймана (строгое гильбертово пространство) и лучшее в формализме Дирака (полезная дельта-функция) внутри одной непротиворечивой математической структуры. С этой целью пытаются пойти дальше гильбертова пространства и включить такие своеобразные объекты, как дельта-функция, но не теряя в то же время хорошей геометрии гильбертова пространства. Решение заключается в рассмотрении структуры вокруг пространства, следуя духу теории распределений: взять обычное гильбертово пространство и оснастить его двумя другими пространствами — одним поменьше и другим побольше, — которые содержат соответственно все хорошие функции (тестовые функции) и все плохие функции (своеобразные функции, такие как δ Дирака). Множество из этих трех пространств называют«оснащенным»гильбертовым пространством, или триплетом Гельфанда.Математические пространства, на которых были построены матричная и волновая механика, были очень разными: одно было дискретным и алгебраическим, другое — непрерывным и аналитическим. Как убедился фон Нейман, нет ничего удивительного в том, что их унификация не может быть достигнута без некоторого насилия над формализмом и математикой. Однако он заметил, что пространства функций, определенных в них, были в основном идентичными. Состояния атома были представлены в матричной механике посредством последовательностей чисел суммируемого квадрата, так что функциональное пространство, которое стояло за этим, было i2, то есть гильбертовым пространством по определению. Волновые функции волновой механики всегда относились к интегрируемому квадрату, то есть принадлежали функциональному пространству Lr И для этих двух пространств действовала теорема Фишера — Риса, хорошо известная математикам с 1907 года и гласящая, что оба эти пространства изоморфны. Так фон Нейман решил головоломку математической эквивалентности квантовых механик, показав, что механика Гейзенберга (сосредоточенная на матрицах и суммах) и механика Шрёдингера (сосредоточенная на функциях и интегралах) математически эквивалентны, поскольку являются вычислениями в двух изоморфных, идентичных гильбертовых пространствах. До этого времени под гильбертовым пространством понималось одно из двух конкретных пространств £2 или Lr Фон Нейман первым задумал абстрактное гильбертово пространство в современном его понимании. Избегая конкретных представлений, он работал с понятиями, полученными из аксиом, и пришел к распространению спектральной теории Гильберта в соответствии с квантовыми потребностями. Гильберт еще в начале века установил основы пространства бесконечной размерности. Но волей судеб такая абстрактная математическая теория, задуманная с опережением в 20 лет, подошла к замку квантовой механики. С тех пор математическая структура квантовой физики сопряжена с гильбертовым пространством. Описание состояния квантовой системы делается через вектор этого пространства. И физические величины изучаются с помощью операторов, определенных в гильбертовом пространстве. В результате появления квантовой механики теория гильбертовых пространств оказалась аксиоматически обоснованной, чему Гильберт был свидетелем.
ГЛАВА 4 Кризис оснований
С развитием математической логики и теории множеств удалось приблизиться к понятию, которое до той поры казалось бесполезным, — бесконечность. Но при этом углубилась трещина, проходящая по основанию математики. Наличие многочисленных парадоксов показало, что здание математики построено на песке. Тогда математики включились в гонку переоснования своей науки. Некоторые ученые встали на сторону логицизма Фреге и Рассела, другие разделились на две непримиримые группы: лидером интуиционистов стал Брауэр, а формалистов возглавил Гильберт. В 1920 году Гильберт направился в беспокойные воды оснований математики и до конца карьеры развивал исключительно эту область. В некоторой степени ученый с удвоенными усилиями возобновил свое исследование оснований математики, хотя на этот раз он был немного более амбициозен, чем 20 лет назад. Он действовал не в одиночку. Его верными оруженосцами стали Пауль Бернайс (1888-1977), один из его ассистентов в Гёттингене, и Вильгельм Аккерман (1896-1962), преподаватель средней школы, его бывший ученик (Гильберт отказался дать ему должность в университете, узнав, что тот намеревается обзавестись семьей, поскольку, по его мнению, это отвлекло бы его от исследовательской деятельности). Важной составляющей этой работы в долгий межвоенный период стали оживленные дискуссии немецкого математика и его ближайших коллег с виднейшими европейскими математиками, которые придерживались противоположных взглядов. Началом размышлений вокруг предмета математики исторически считается последняя четверть XIX века. Однако любопытство в отношенииприроды математического знания не ново, ему 2000 лет. Первый кризис оснований произошел в Древней Греции, когда разрушилась пифагорова арифметика. Пифагорейцы полагали, что все числа рациональны, но вскоре выяснилось, что существуют также иррациональные числа (как V2). Открытие этих неизмеримых чисел вызвало раскол в их математике. Рациональные числа не полностью описывали действительность. Континуум действительных чисел (например, прямая) образован не дискретным набором индивидуальных атомов. Работы Евдокса (IV век до н.э.) по обоснованиям примирили сознание с иррациональной бесконечностью и заложили фундамент, на котором была воздвигнута евклидова геометрия. Работы, связанные со вторым кризисом оснований, уже в XX веке разъясняли, в чем заключаются метод, строгость и истина новой математики — скорее аксиоматичной, чем интуитивной, скорее экзистенциальной, чем конструктивной. Нужно понимать, что не избежал Гильберт и подводных камней. В их числе выделим ряд антагонических понятий математики, которые возникли не из ничего, а уходят корнями в историю развития самой точной из наук. Распространение математического анализа с начала XIX века, наряду с зачатками теории множеств и математической логики, — это путеводная нить дисциплины, которая стала называться философией, или основаниями математики. Но вернемся на некоторое время к истокам.БОГ — МАТЕМАТИК?
Платонизм — изначальная философия математики. Приверженцами этой позиции среди прочих были Платон, Кантор, Гёдель... Любопытно, что первым платоником был не Платон, а Пифагор, который слепо верил, будто все есть число и математические объекты реально существуют. Как числа, так и треугольники или окружности существуют сами по себе, независимо от их толкования и нашего представления о них. Неоплатоники во главе с Блаженным Августином (IV век) утверждали, что бесконечное количество чисел в действительности существует в божественном разуме. И кому хватило бы глупости утверждать, будто Бог прекращает счет на каком-то числе, каким бы большим оно ни было? Перенесение термина платонизм из области философии в математику произошло на лекции, которую в 1934 году читал Пауль Бернайс, первый помощник Гильберта. Бернайс хотел дать возбуждающее интерес название способу восприятия современной математики, в которой математические объекты не строятся, а понимаются как заданные. Для Кантора, например, реальность чисел была намного ощутимее реальности чувственного мира, поскольку числа существуют в виде вечных идей божественного интеллекта. Гёдель пошел еще дальше и рассматривал математические множества как объекты настолько же реальные, как и физические тела. Математики-платоники, имя которым легион, не изобретают математические теоремы, а открывают их. Недостаток платонизма заключается в том, что он перенаселяет небеса. Платонизм хорош, когда необходимо утверждать, будто реально существуют простые математические сущности (треугольник в целом, квадрат в целом или общее количество натуральных чисел). Но он рушится, едва мы оставляем в стороне объекты античной математики и обращаемся к надуманным объектам современной математики — классам, множествам, функциям и сложным абстрактным структурам, которые выходили на первый план в XIX веке.ЛАБИРИНТ ВЫЧИСЛЕНИЙ
Греки основали геометрию и подчинили ей арифметику. Но благодаря алгебре постепенно арифметика стала независимой от геометрии, что 2000 лет спустя дало возможность осуществить обратное приведение. Геометрия нашла свое место в алгебре, которая, в свою очередь, располагалась в арифметике, усиленная новым исчислением Ньютона и Лейбница. Но арифметизацию математики, произошедшую между XVII и XVIII веками, требовалось вернуть к греческой строгости и положить конец фокусам исчисления бесконечно малых. В начале XIX века мрак математического анализа был почти абсолютным. Огюстен-Луи Коши (1789-1857) порвал с традицией бесконечно малых и переосновал анализ на понятиях предела и функции. Понятие функции было уточнено одновременно с развитием теорий дифференцирования и интегрирования. Но «Курс анализа» Коши, который увидел свет в 1821 году, строился на понятии непрерывности. Как вычисление пределов, так и работа с функциями требовали выверенного определения континуума чисел, на основе которого производились операции. Но что же представляет собой континуум? Доказательствам основных теорем анализа требовалось предварительное доказательство непрерывности прямой действительных чисел. Те, кто преподавал анализ, не знали верных доказательств теорем и пытались сделать так, чтобы официальные мистические операции принимались на веру. Это происходило даже с базовой теоремой Больцано, гласящей, что если функция непрерывна на определенном отрезке и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где эта функция равна нулю. Нечто подобное происходило в то время и с геометрией, и именно Гильберт прояснил понятие непрерывности. В середине XIX века основная проблема состояла в том, чтобы построить действительные числа (континуум) на основе рациональных чисел, поскольку было известно, как построить последние на основе целых, а целые — на основе натуральных. Натуральные, целые, рациональные, действительные... всю математику. В 1872 году были предложены несколько теорий построения действительных чисел. Во-первых, это теория действительных чисел: ее смогли воспроизвести на основе конспектов занятий Вейерштрасса, который идентифицировал каждое действительное число с бесконечной суммой рациональных чисел. Во-вторых, это теория Кантора, аналогичная теории Шарля Мерэ (1835-1911), в которой каждое действительное число — предел последовательности рациональных чисел. И наконец, это теория Дедекинда, в которой действительное число — всего лишь сечение, оно подразумевает разделение всех точек прямой на два класса: расположенные слева и справа от сечения. Для любого сечения на прямой всегда есть действительное число, которое делит прямую на две части. Если Платон утверждал, что бог вечно геометризует, то Дедекинд объявил, что человек вечно арифметизирует. Все числа свелись, по сути, к натуральным. Это настоящий интеллектуальный подвиг. Но что такое натуральные числа?ЛОГИКА КАК УНИВЕРСАЛЬНЫЙ КЛЮЧ К МАТЕМАТИКЕ
Поскольку арифметика напоминала дерево, которое безустанно растет вверх, в то время как его корни уходят вглубь, возникло первое течение, связанное с основаниями, — логицизм. Познакомимся с ним и с его первым идеологом, Готлобом Фреге (1848-1925). Этот немецкий математик отстаивал идею, что вся математика базируется на натуральных числах. Но как их построить? Ключ был, по его мнению, в области логики. Всю жизнь Фреге был угрюмым преподавателем в Йенском университете. Учеников у него было так мало, что регулярно его занятия посещали только двое: один философ и один военнослужащий в отставке, который учился для души. Он был неспособен говорить на другие темы, кроме логики и математики, и всегда тактично сводил любой разговор к ним. Результатом этой одержимости была «Концептография», опубликованная с подзаголовком «Подражающий арифметике формальный язык чистого мышления» в 1879 году. Фреге наполнил новым вином старые бурдюки логики, создав «математическую логику». Традиционная логика пребывала не в лучшем состоянии, несмотря на то что, по-видимому, исчерпала себя еще при Аристотеле. Но логика начала лукавить с математикой. Раймунд Луллий (1232-1315) в Ars Magna и Хуан Карамуэль (1606— 1682) в Mathesis Audax задумали вид логической алгебры, в которой все рациональные истины понимались в рамках вида вычислений универсальной записи, названной Лейбницем как calculus ratiocinator. Философы больше не испытывали необходимости в полемике, иначе они решали бы их, как будто их можно вычислить. Они усаживались бы за свои столы, брали в руки перья и говорили друг другу: посчитаем! Эти семена проросли в алгебру логики, которую Джордж Буль (1815-1864) вывел в своих «Законах мышления» в 1854 году. Но Фреге больше интересовался логикой алгебры, чем алгеброй логики, и в своей «Концептографии» формализовал логику пропозиций и предикатов (логику первого порядка), то есть рассуждений о некоторых объектах и свойствах, удовлетворяющих этим объектам, но не о свойствах, которые проверяют такие свойства (это епархия логики второго порядка). Позже в «Основах арифметики» (1884) он заложил базу программы логицизма, которую последовательно изложил в томах «Основных законов арифметики, выведенных концептографически» (1893-1903). Фреге утверждал, что логика предшествует математике и, следовательно, математические понятия должны быть сведены к логическим. Математика — лишь дополнение к логике. Значит, арифметика была логикой в последней инстанции, и арифметические понятия должны быть проанализированы в чисто логических терминах: «вычислить значит вывести». Говоря словами Фреге, «арифметические предложения — это логические законы, хотя не первичные, а производные». Если упростить окаменелую строгость работ Фреге, в которых педантичности и точности поровну, можно сказать, что он пришел к определению чисел с помощью классов, то есть с помощью множеств, или ансамблей. Каждому натуральному числу соответствовал класс всех классов, которые были подобны (равномощны) заданному. Например, число 3 — это то, что есть общего у всех следующих классов: лепестки трилистника, цвета светофора и так далее. Таким образом, число 3 может быть идентифицировано классом всех этих классов. В целом Фреге идентифицировал число 0 с классом всех пустых классов, 1 — с классом всех одночленных классов, и так далее. И поскольку есть только одно пустое множество (которое обозначается как перечеркнутый кружок, здесь заменен Ǿ), 0 = Ǿ. Тогда число 1 определяется как класс из всех классов, равномощных классу [Ǿ], обладающий единственным элементом. Аналогично определялись остальные числа.АКСИОМЫ ПЕАНО
В 1888 году Рихард Дедекинд опубликовал книгу с привкусом логицизма «Что такое числа и для чего они служат»(Гильберт прочитал ее в молодости). Однако Дедекинд определил натуральные числа принципиально иначе, чем Фреге. В 1889 году в книге под названием «Принципы арифметики, изложенные согласно новому методу» итальянский математик Джузеппе Пеано подтвердил аргументы Дедекинда, хотя и не был знаком с его работой, и определил натуральные числа посредством трех первоначальных понятий (нуль, функция последующего члена и равенство) и пяти аксиом. 1. Нуль есть натуральное число. 2. Следующее за натуральным числом есть натуральное число. 3. Нуль не следует ни за каким натуральным числом. 4. Всякое натуральное число следует только за одним натуральным числом. 5. Если какое-либо предложение доказано для нуля и если из допущения, что оно верно для натурального числа А, вытекает, что оно верно для следующего за А натурального числа, то это предложение верно для всех натуральных чисел. Пятая аксиома получила название принципа индукции и является основополагающей для доказательства теоремы о натуральных числах без необходимости проверять каждое из них по одному. Принцип формализует интуитивное представление о том, что когда все фишки домино выстроены в одну линию, падение первой из них (нуля) предполагает падение всех остальных (всех натуральных чисел). На основе этих аксиом можно определить сложение и умножение натуральных чисел, а также расположить их в упорядоченном виде. Результат известен как арифметика Пеано. Джузеппе Пеано, около 1910 года.
Джузеппе Пеано, около 1910 года.
К несчастью, смелая программа Фреге была поставлена под сомнение из-за обилия логических парадоксов. В своих работах Фреге всегда исходил из принципа выделения, согласно которому каждому понятию можно назначить его расширение, то есть любое свойство определяет класс элементов, которые удовлетворяют этому свойству. Аксиома существования классов была «Базовым Законом V» «Основных законов арифметики», и именно ею объясняется широкое распространение логицизма Фреге. В письме от 16 июня 1902 года молодой математик Бертран Рассел (1872-1970) проинформировал преподавателя Фреге о том, что в рамках его системы на основе этого несчастного закона может быть выведено противоречие. Парадокс Рассела показывал, что назначение каждому свойству связанного с ним класса было делом рискованным. Узнав об этом противоречии, Фреге добавил приложение ко второму тому «Основных законов арифметики», в котором попытался спасти свой огромный труд, ограничив применение принципа выделения. Вскоре он понял, что от этого мало проку, и остановил публикацию третьего тома своей главной работы. Он так и не оправился от удара. Погрузившись в меланхолию, без всякой надежды, но и без страха он признавал катастрофу: «Нет для ученого ничего ужаснее, чем выяснить, что все основание его работы рушится, именно в тот момент, когда он эту работу заканчивает. Меня в эту ситуацию поставило письмо господина Рассела, моя работа была почти готова к печати». Продемонстрировав интеллектуальную целостность, которой Рассел восхищался всю жизнь, Фреге ответил последнему, что арифметика, а с ней и вся математика вновь пошатнулись. Здравого смысла не было достаточно для поддержания безопасности математики перед лицом угроз, исходящих от логики.
ОБИЛИЕ ПАРАДОКСОВ
До весны 1901 года, когда Рассел обнаружил свой парадокс, согласно Фреге, считалось, что каждому свойству соответствует один класс, который образован сущностями, обладающими этим свойством. Рассел изучал поведение собственных классов, то есть тех, которые являются членами самих себя. Например, класс всех классов (который, являясь другим классом, принадлежит сам себе) или класс всех понятий (являясь другим понятием, также принадлежит сам себе). Логические огрехи неизбежны: если в библиотеке поместить имеющий черную обложку каталог всех книг в библиотеке, у которых имеется черная обложка, этот каталог каталогизирует сам себя. Возьмем класс R всех классов, которые обладают свойством не быть членами самих себя, формально: R = [х: х /ϵ х], где ϵ — символ принадлежности (/ϵ здесь замена перечеркнутого ϵ). И зададимся вопросом, является ли R членом самого себя, если R ϵ R. Мы выясним, что любой ответ сразу же предполагает противоположный ответ. Если это так, то это не так. Если это не так, то это так. Действительно, если R ϵ R, то есть если R принадлежит самому себе, то, по определению, R /ϵ R, то есть R не принадлежит самому себе, поскольку это класс всех классов с этим свойством. Но и наоборот, если R /ϵ R, то R ϵ R, поскольку оно выполняет свойство, определяющее класс всех классов, которые не являются членами самих себя. В итоге получается противоречие: R ϵ R только тогда, когда R /ϵ R. Класс R принадлежит самому себе только тогда, когда он не принадлежит самому себе. Рассел был в недоумении от абсурда, с которым он столкнулся. Этому противоречию он затем дал название парадокса брадобрея: цирюльник в деревушке утверждает, что бреет всех мужчин, которые не бреются сами, и никого больше. В один прекрасный день, проснувшись, он задается вопросом, кто же бреет его, и в замешательстве осознает, что бреет сам себя тогда и только тогда, если не бреет сам себя. Бедный цирюльник попадает в настоящее логическое болото. Французский математик Анри Пуанкаре был первым, кто указал на то, что источник парадоксов, атакующих логику, заключается в цикличности, в виде автореференции или принадлежности самому себе. Парадоксы держались на использовании непредикативных определений — тех, в которых определяемое входит в состав определения. Позже Рассел назвал это принципом порочного круга. Неудивительно, что нарушение этого принципа ведет к парадоксам, антиномиям и противоречиям, многие из которых признаются даже вне формальных языков, в естественных языках. В качестве примера служит хорошо известный парадокс лжеца, приписываемый Эпимениду Критскому (в своих письмах о нем упоминает даже святой Павел). В одном из стихотворений Эпименид порицает критян, называя их лжецами. Но поскольку он сам критянин, его утверждение, относящееся к самому себе, преобразуется в «я лгу». В этом случае то, что он говорит, не может быть правдой, значит, критяне не лгут. Но если они не лгут, то и Эпименид тоже, поэтому получается, что критяне лгут, и так далее. Математическая логика, как ее стали называть вслед за Пеано, создавала одни только неприятности. И Пуанкаре, который считал ее бесполезной, смеялся: «Она уже не стерильна, она порождает противоречия». Несмотря ни на что логистическая программа, составленная Фреге, получила развитие благодаря бесцеремонности Бертрана Рассела и Альфреда Норта Уайтхеда (1861-1947). В 1900 году на международном конгрессе по философии, проходившем в Париже, Рассел столкнулся с символической реформой Пеано. В 1889 году Пеано представил свои «Принципы арифметики», содержащие знаменитые пять аксиом (включая принцип индукции) для натуральных чисел, используя новую символику, которую разработал сам. В сообществе логиков и математиков одномерная символика Пеано была принята лучше, чем двумерная символика Фреге (за исключением его учеников, которые взбунтовались и не успокоились, даже когда Пеано предложил поставить всем зачет). В 1902 году, верный логицизму Фреге и символизму Пеано, Рассел опубликовал «Принципы математики». Но медовый месяц логики был коротким, потому что незадолго до публикации он открыл парадокс, который сегодня носит его имя. До 1910 года Рассел работал с Уайтхедом, и оба стремились справиться с противоречиями, которые вскрыл парадокс. В книге Principia mathematica (1911-1913) они глубже, чем кто-либо на сегодняшний день, погрузились в основания математики. Эта блестящая работа стала, говоря словами Гильберта, «коронацией аксиоматизации».БЕСКОНЕЧНЫЙ ОТЕЛЬ ГИЛЬБЕРТА
Гёттингенский профессор придумал метафору, которая просто и ясно объясняет некоторые парадоксы, связанные с бесконечностью и открытые математиками одновременно с логическими парадоксами. Несмотря на то что это кажется невероятным, в отеле с бесконечным числом номеров всегда есть место для новых гостей, хотя все номера заняты. Действительно, если мы переселим гостя из первого номера во второй, того, что во втором, — в четвертый, того, что в третьем, — в шестой, и так далее, мы освободим все нечетные номера. Поскольку существует бесконечное количество нечетных чисел, есть место не только для нового постояльца, который подойдет к гостиничной стойке, но также и для бесконечного числа постояльцев. Из этой же самой ситуации мы могли бы сделать больше удивительных выводов... — В отеле заняты все номера, и один гость уезжает. Тогда число постояльцев остается тем же самым (бесконечным). — Если уезжают все гости, занимающие четные номера, то число постояльцев остается тем же самым (бесконечным). — Однако если из отеля уедут все гости, занимающие номера, например с пятого и далее, то число постояльцев не будет тем же самым (в этот раз их число будет конечным). Все это наводит нас на мысль о гибкости математической бесконечности и об осторожности, с которой нужно высказываться о ней.Чтобы избежать парадоксов, Рассел и Уайтхед сформировали теорию типов, в которой для того, чтобы X ϵ Y было правильно составленной формулой, требуется, чтобы тип значения Y был непосредственно выше типа значений X. Таким образом, пропозиция «класс всех стульев не является стулом» — не истинная и не ложная, а попросту лишена смысла, поскольку стульями могут быть только объекты, а не классы объектов. Другими словами, ошибочно распространять свойство одного типа на другой. При применении этой хитроумной теории авторы могли утверждать, что формулировки, ведущие к парадоксу Рассела, перестают иметь смысл: R ϵ R теперь являлось неправильно составленной формулой, поскольку в ней было задействовано не больше одного типа.
Математика [...] обладает не только истиной, но и высшей красотой, холодной и суровой, подобной скульптуре. Бертран Рассел
В Principia после устранения парадоксов Уайтхед и Рассел перешли к выведению математики из логики, поскольку в их понимании граница здесь невозможна. С технической точки зрения проект логификации математических теорем натолкнулся на многочисленные трудности. Ученым потребовалось более 379 страниц (!), чтобы доказать, что 1 + 1 = 2. Настоящее безумие. Кроме того, они были вынуждены расширить логику до крайне обобщенной теории отношений, в которую включили такие малоудовлетворительные аксиомы, созданные для данного случая, как редуктивность и бесконечность. Неуклюжая аксиома редуктивности работала как нечто вроде deus ex machina, — авторы прагматично обосновывали ее тем, чтобы работать с антиномиями и логифицировать математику: когда формула оказывается слишком сложной, предполагалось, что ее всегда можно упростить до другой, более низкого уровня. Аксиома бесконечности была нужна для определения натуральных чисел в комплексе. Следуя за Фреге, они определили 2 как класс всех пар, 3 — как класс всех троек... Но они были вынуждены ввести аксиому (в ней утверждалось, что для любого числа существует другое, больше него), обоснование которой не могло строиться ни на одном из классов логической или математической догадки (что было бы нарушением принципа «логика или математика, основывающаяся на самой себе»), а лишь на характерной структуре мира, которому приписывалось то, что он должен включать в себя бесконечное число объектов. Если бы в мире существовало не бесконечное число вещей, а только максимальное число вещей n, Рассел и Уайтхед не смогли бы определить число n + 1, поскольку класс всех скоплений (n + 1) был бы пустым, так как не было бы n + 1 объектов в мире. Герман Вейль, ученик Гильберта, решительно отверг это: «Принципы...» испытывали веру, как Отцы Церкви. Баланс заключался в том, что в лучшем случае Расселу и Уайтхеду удалось свести математику к виду мегалогики, раю для логиков. Логистический тезис является либо ложным (если логика не включает в себя теорию классов — то, что называется теорией множеств), либо тривиальным (если включает ее). На сегодняшний день некоторые логики пытаются возродить этот тезис, чтобы перевести математику в подходящую логику второго порядка (поскольку логики первого порядка оказалось недостаточно). Но, как говорили многие математики, логика второго порядка — это всего лишь замаскированная математика множеств. Так как в логике второго порядка допустимо говорить не только об объектах, но и о свойствах, можно определить множество понятий, типичных для теории множеств. Количественно оценивать свойства — в конечном итоге все равно что количественно оценивать множества, множество объектов, выполняющих свойство. Следовательно, речь идет о логике, лежащей в основе собственно теории множеств. Ее наибольшая выразительная сила, позволяющая охарактеризовать бесконечность или формализовать принцип индукции в одной-единственной аксиоме (вместо схемы аксиом, заключающей в себе бесконечности), — это обоюдоострое оружие. Мы находимся там же, где и были: если логика включает в себя теорию множеств, то логистический тезис истинный, но тривиальный; если логика его не включает, он радикально ложный.
РОЖДЕНИЕ ТЕОРИИ МНОЖЕСТВ
Логики шли на невероятные хитрости, чтобы решить проблему парадоксов. Но какое решение давали математики? Если логики хотели логифицироватъ математику, то математики хотели омножествитъ ее. Омножествление математики началось издалека. Абстрактная теория множеств была создана Кантором, но связанный с множеством подход в математике предшествовал ей. Он присутствовал у Римана и в основном у Дедекинда. Риман предложил понятие многообразия в значении, граничащем со значением множества, в качестве основания всей чистой математики. И Дедекинд выдвинул подход множеств к алгебре, введя такие понятия, как группа, тело и идеал (только понятие кольца не поддалось ему и было введено позже Гильбертом). Героическая эпоха теории множеств начинается в 1872 году. Тогда, опубликовав свои построения действительных чисел, Дедекинд и Кантор приступили к бурному личному взаимодействию. В 1874 году Кантор доказал, что существует два типа бесконечности: счетная (как множество натуральных чисел) и несчетная (как действительные числа, то есть как континуум). Он заявил, что множество алгебраических чисел счетное, и доказал это на основе метода, который Дедекинд передал ему в письме, хотя и не признал здесь заслуги последнего (этот конфликт, скорее всего, и стал причиной их разрыва). В 1879 году Кантор представил понятие кардинального числа множества, которое обобщает понятие числа элементов множества в области бесконечных множеств. Проверка того, обладают ли два конечных множества одним и тем же числом элементов, состоит в одновременном удалении по одному элементу из каждого из них столько раз, сколько возможно. Если оба множества заканчиваются одновременно, мы точно знаем, что у них одно и то же число элементов, или кардинальное число. Так как эта идея не предполагает счета, она распространяется на бесконечные множества: о множествах A и В говорят, что они имеют одно и то же кардинальное число, и это записывается как |A| = |B| если между ними можно установить биекцию, то есть соответствие один к одному.ДИАГОНАЛЬНЫЙ АРГУМЕНТ КАНТОРА
Одним из великих открытий Георга Кантора стали несчетные множества, для которых невозможно провести биекцию с натуральными числами. Одно из них — это континуум. И если целые и рациональные числа счетные, то действительные числа такими не являются. Нельзя связать их попарно с натуральными числами, их нельзя пронумеровать, поставить в список одно за другим. Возьмем числовую прямую и рассмотрим отрезок от 0 до 1. Выразим все входящие в этот отрезок числа в двоичном коде, то есть с помощью последовательностей 0 и 1. Например: 101001000... (опустив 0 и запятую, отделяющую десятичную дробь, которые должны предшествовать выражению). Докажем, что предположение о том, что это счетное множество, приводит к противоречию. Действительно, если бы это было так, мы могли бы записать все его элементы в списке, подобном следующему: 1.° → 0100... 2.° → 0110... 3.° → 1101... ... ... Теперь обратим внимание на элементы главной диагонали, они подчеркнуты. Построим элемент, который несмотря на то, что является последовательностью 0 и 1, не входит в список. Для этого образуем последовательность, состоящую из следующих чисел: так как первый выделенный член был 0, запишем 1; так как второй был 1, запишем 0; так как третий был 0, запишем 1; и так далее. Итоговый элемент начинается с 101... и не совпадает ни с одним из элементов в списке. Это не может быть первая последовательность, поскольку первый член отличается, не вторая, потому что мы изменили второй член, и не третья, и так далее. Это противоречит предположению, что речь идет о счетном множестве, которое, следовательно, может быть выражено в виде списка. Использованный метод доказательства получил название диагонализации и повлиял на последующие значимые доказательства в истории оснований математики. Георг Кантор.
Георг Кантор.
Между тем Дедекинд дал более удачное определение бесконечному множеству, чем Кантор. По прошествии времени оба определения, избавленные от ошибок, оказались равносильными (в соответствии с аксиомой выбора, о которой речь пойдет позже). Для Кантора множество бесконечно, если оно не конечно, то есть если нельзя провести биекцию с каким- нибудь натуральным числом. Для Дедекинда, наоборот, под влиянием предположений Галилея и Больцано, множество бесконечно только тогда, когда можно провести биекцию с его собственной частью. Например, натуральные числа бесконечны, потому что можно провести биекцию с четными числами, при этом 0 соответствует 0; 1 - 2; 2 - 4; и в целом каждому числу n — вдвое большее число 2n.
Его теория представляется мне наиболее заслуживающим удивления цветком математического духа и вообще одним из высших достижений чисто умственной деятельности человека. [...] Никто не изгонит нас из рая, который создал нам Кантор. Давид Гильберт о Георге Канторе, «О бесконечном» (1925)
К концу 1882 года Кантор разработал свою арифметику кардинальных и порядковых (трансфинитных) чисел, а также выдвинул континуум-гипотезу. Натуральные числа образуют бесконечное множество наименьшего размера, который мы можем вообразить. Следовательно, его кардинальное число, то есть первое бесконечное кардинальное число, обозначается буквой алеф еврейского алфавита с нижним индексом 0: ϰ0. Это кардинальное число соответствует всем счетным множествам, и это первая веха на пути к бесконечности. Кардинальное число континуума, действительных чисел, равно (по ряду сложных причин) 2ϰ0. При таких условиях континуум-гипотеза устанавливает, что нет никакой другой бесконечности между натуральными и действительными числами, или, говоря другими словами, что 2ϰ0 =ϰ1 Последовательность кардинальных чисел ϰ0, ϰ1, ϰ2,... работает как своего рода модель для измерения размера вселенной множеств, где существует бесконечное число бесконечностей. Безрезультатные попытки доказать континуум-гипотезу и постоянные нападки Кронекера на теорию трансфинитных множеств спровоцировали у Кантора депрессию, которая отдалила его от математики и подтолкнула в сторону теологии (он также увлекался идеей, что Бэкон был истинным автором произведений Шекспира). С 1900 года теория Кантора, как и логика, стала мостом над бурными водами. Параллельно с логическими парадоксами возникли антиномии теории множеств. Большинство парадоксов, в которых говорилось о классах, были переформулированы с помощью теории множеств (например, парадокс Рассела). Но появились и новые: парадоксы бесконечности. В то время как логические парадоксы были связаны с цикличностью определения некоторых классов, парадоксы множеств отсылали к бесконечности. Главный в их числе — парадокс Кантора о собрании всех множеств. Пусть V — «множество» всех множеств. Поскольку, как доказал Кантор, кардинальное число любого множества меньше кардинального числа его показательного множества (которое обозначается ϑ(A) и включает в себя все подмножества или части A), получается, что |V| < |ϑ(V)|. С другой стороны, из определения V следует, что показательное множество V должно содержаться в V, поскольку V — это абсолютное множество, самое большое, которое включает в себя все остальные, и нет ничего выше него. Поэтому |V| ≥ |ϑ(V)|, что является абсурдом, противоречием по отношению к предыдущему результату. Эрнст Цермело (1871-1953) был первым математиком, который различил нелогистический выход из лабиринта (не зря он открыл парадокс, подобный парадоксу Рассела): следовало перейти от интуитивной к аксиоматической теории множеств. С 1897 года Цермело находился в Геттингене и выполнял инструкции Гильберта, который воодушевил его сформулировать систему аксиом для теории Кантора. Его вклад в аксиоматический метод теории множеств сравним с вкладом Гильберта в геометрию. В 1908 году Цермело представил первую аксиоматизацию теории множеств, отшлифованную Абрахамом Френкелем (1891-1965) в 1922 году (и фон Нейманом в 1925 году, когда тот включил в нее аксиому регулярности, или основания).
КЛАССЫ И МНОЖЕСТВА
Теория множеств Цермело — Френкеля также исходит из логики первого порядка и принимает отношение принадлежности ϵ в качестве первоначального. Аксиомы ZF, озвученные вербально, следующие. 1. Два множества равны тогда и только тогда, когда они имеют идентичные элементы (аксиома объемности). 2. Существует множество без единого элемента Ǿ. 3. При заданном множестве х и свойстве, которое можно сформулировать на языке первого порядка теории множеств, существует множество всех элементов X, которые удовлетворяют свойству (аксиома выделения). 4. Если x и у — множества, то неупорядоченная пара {х, у} — множество. 5. Объединение множеств во множество — множество. 6. Можно образовать потенциальное множество любого множества, то есть собрание всех подмножеств или частей любого множества — другое множество. 7. Существует как минимум одно бесконечное множество (аксиома бесконечности). 8. Образ множества, заданный функцией, является множеством (аксиома преобразования). 9. x не принадлежит x (аксиома основания, или регулярности). Если к этим аксиомам добавить так называемую аксиому выбора, получится система ZFC (С — от английского choice — «выбор»). В 1930-е годы теория множеств ZFC была расширена теорией классов и множеств фон Неймана — Бернайса — Гёделя (известной среди математиков по аббревиатуре NBG). Фон Нейман предложил иерархическую и накопительную конструкцию вселенной множеств, которую обычно схематично представляют в виде перевернутого конуса (см. рисунок). На основе пустого множества, путем повторения (с помощью трансфинитной рекурсии) операций «части множества- и «объединение множества- он построил все этажи, на которых упорядоченно располагаются множества — от самых маленьких до самых больших: 0 = Ǿ, 1 = {0} = {Ǿ}, 2 = {0, 1} = {Ǿ, {Ǿ}} и так далее. В этой теории парадоксы Рассела и Кантора доказывают, что R и V — не множества, а классы, которые принимаются в рамках этой теории. Кофинальные элементы, обладающие иерархией, не являются членами никакого другого множества, потому что они слишком большие и соответствуют классам. Иерархическая конструкция вселенной множеств, разработанная фон Нейманом.
Иерархическая конструкция вселенной множеств, разработанная фон Нейманом.
С тех пор она известна как аксиоматика ZF (по их инициалам) теории множеств. Итак, в ZF парадокс класса Рассела превращается в доказательство того, что этот класс не является множеством, другими словами, что его не существует в рамках этой теории, в связи с чем антиномия испаряется в воздухе. Если мы предположим, что R — это множество, и столкнемся с абсурдом, это будет означать, что R — не множество. Аналогично, парадокс Кантора превращается в доказательство того, что «множество» всех множеств V — это не множество, поэтому его также не существует внутри теории. В ZF такая загадка, как парадокс брадобрея, демонстрирует отсутствие существования индивидуума с этими характеристиками. Более того, аксиомы ZF блокируют цикличность, которая с помощью различных стратегий делает очевидной несостоятельность парадоксов. Формулы типа R ϵ R запрещены в ZF, поскольку в аксиоме основания, или регулярности, установлено, что ни одно множество не принадлежит самому себе, то есть (перевернутое A)x(x /ϵх). При этой аксиоме опасных множеств просто не существует. Следует заметить, что при наличии ZF не только были устранены парадоксы неформальной теории множеств, но и стало возможным омножествление математики: с определением функции как множества упорядоченных пар, предложенным Феликсом Хаусдорфом (1868-1942) и Казимиром Куратовским (1896-1980) чуть позже, это понятие (столп анализа) оказалось омножествленным, что упрочило обоснование математики с помощью множеств. Все головокружительное разнообразие математических структур оказалось сведено к их самым базовым компонентам — множествам. Однако работы Цермело вызвали большой ажиотаж и крайне враждебную реакцию специалистов. Пытаясь доказать континуум-гипотезу, в 1904 году Цермело сформулировал аксиому выбора. Эта аксиома гласит, что можно одновременно выбрать элемент каждого множества из бесконечного собрания непустых множеств. Формально если S = {А, B, С,...} — это собрание непустых множеств, то существует множество Z, которое состоит ровно из одного элемента множества А, одного из B, одного из С и так далее. Бертран Рассел объяснял это на следующем примере. Представим себе миллионера, который, каждый раз покупая пару туфель, покупает и пару носков. Предположим, он уже обладает бесконечным набором коробок с туфлями и таким же количеством упаковок с носками. Если бы он хотел удостовериться, что у него действительно равное количество пар туфель и носков, он мог бы доставать по одному правые туфли и находить им пару из одного носка (или если бы коробки с туфлями и неоткрытые упаковки носков закончились одновременно, он бы знал, что их у него одинаковое количество). Но он не может совершить последнее действие, не применив аксиому выбора, поскольку эта аксиома позволяет осуществлять бесконечное число произвольных выборов в коллекции наборов носков (в то время как из каждой коробки туфель он всегда может выбрать правый, между носками нет никакой разницы, поскольку не существует правого носка, отличного от левого). Несмотря на кажущуюся невинность, аксиома выбора имеет удивительные следствия, противоречащие интуиции. Одно из них, по примеру Цермело, — это принцип вполне упорядочивания, который гласит, что любое множество, каким бы странным оно ни казалось, может быть вполне упорядоченным, то есть упорядоченным линейно, как натуральные числа, где любое подмножество всегда обладает первым элементом. Более того, аксиома выбора вскоре оказалась необходимой для доказательства того, что арифметика кардинальных чисел работает корректно (что два любых кардинальных числа всегда сравнимы), а также для доказательства через лемму Цорна многочисленных базовых результатов алгебры и анализа. Это спровоцировало международную дискуссию между сторонниками и противниками аксиомы выбора (это даже нашло отражение в специальном номере журнала Mathematische Annalen, издаваемого Клейном и Гильбертом). С одной стороны, этот мощный инструмент защищали Цермело, Рассел и Гильберт. С другой — против его необоснованного использования боролся молодой нидерландский математик Лёйтзен Эгберт Ян Брауэр (1871-1956), который рассчитывал на поддержку важных французских математиков: Рене-Луи Бэра (1874-1932), Эмиля Бореля (1871-1956) и Анри Лебега (1875-1941). Если на островах главенствовали логицисты, то на континенте буйствовали формалисты — под предводительством Гильберта — и интуиционисты, во главе которых стоял Брауэр.
БРАУЭР ПРОТИВ ГИЛЬБЕРТА
Брауэр заявлял, что «пируэты Цермело» способствуют прочному обоснованию математики раз и навсегда. Его беспокоило то, что последние 25 лет абстрактная математика возводила воздушные замки. Ему нельзя отказать в проницательности в том, что касается рисков аксиомы выбора. Благодаря ей были извлечены на свет многочисленные математические монстры. И в их числе, несколькими годами позже (в 1926 году), парадокс Банаха — Тарского. Теорема, стоящая за ним, обязательно использует эту сомнительную аксиому и производит следующее парадоксальное распределение множеств в трехмерном пространстве: шар можно разложить на конечное число отдельных частей, так что на их основе можно вновь построить два шара, идентичных исходному. Это такой математический аналог библейского чуда хлебов и рыб (единственное, что сочетается со здравым смыслом, — то, что оба шара, идентичных исходному, не измеряются в понимании Лебега, поэтому данный парадокс никогда не появляется при вычислении объемов). В 1907 году Брауэр получил степень доктора наук в Амстердамском университете, защитив диссертацию «Об основаниях математики», в которой наблюдались интуиционистские черты. Через пять лет, 14 октября 1912 года, уже получив признание как математик, с огромным профессиональным багажом за спиной, он прочитал лекцию под названием «Интуиционизм и формализм». Эта лекция обозначила начало его плана по обоснованию математики, и сразу же на нее навесили ярлыки «интуиционизм» и «формализм». В этой лекции Брауэр отсылал к Канту, Кронекеру и недавно скончавшемуся Пуанкаре (самой яркой из «звезд») как к своим предшественникам.КРИВАЯ ГИЛЬБЕРТА
В 1877 году Кантор построил биекцию между отрезком и квадратом. В отрезке было столько же точек, сколько и в квадрате. Возможность установить соответствие по одному между одномерной прямой и двумерной плоскостью заставила его воскликнуть: «Я это вижу, но я в это не верю!» Дюбуа-Реймон пошел еще дальше и заявил, что это «противно здравому смыслу». С1890 по 1891 год Пеано и Гильберт вообразили соответствующие непрерывные кривые, способные пройти через каждую точку квадрата. Кривые Пеано и Гильберта (одномерные линии, способные заполнить двумерные квадраты) только усугубили проблему размерности. Как различить «измерения»? Пуанкаре подчеркнул необходимость надлежащего определения измерения.Брауэр и топология
С 1908 по 1911 год Брауэр взял паузу в жестокой борьбе за интуиционизм и заложил основы новой математической дисциплины — топологии, «геометрии на резиновом листе» (как выразился Пуанкаре). Для начала он предложил несколько контрпримеров, о которые разбивались большинство результатов, полученных Артуром Шёнфлисом (1853-1928), другом Гильберта. И уже в 1911 году он представил теорему об инвариантности размерности с помощью бинепрерывного приложения, то есть гомеоморфизма, что положило конец сомнениям, зароненным Кантором, Пеано и Гильбертом: m-мерное и п-мерное пространства негомеоморфны, если m отличается от n. Они могут поддаваться биекции, но никогда не гомеоморфны, потому что эта биекция не будет непрерывной. Топология демонстрировала торжество здравого смысла. После каждой итерации кривая Г ильберта змеится все больше и больше, прежде чем (в пределе) полностью покрыть квадрат.
После каждой итерации кривая Г ильберта змеится все больше и больше, прежде чем (в пределе) полностью покрыть квадрат.
Вклад Гаусса, Римана и, наконец, Гильберта позволил геометрии окончательно освободиться от наследия Евклида и Канта (несмотря на протест Фреге). Брауэр предложил отказаться от априорного подхода Канта к пространству, но более решительно придерживался априорного подхода ко времени. Математика ведала свойствами времени, поскольку его ход сводился к арифметической последовательности: 0, 1, 2, 3, 4... 1 после 0, но до 2, и так далее. Согласно Брауэру, нужно было восстановить конструктивистское видение математики Пуанкаре. Несмотря на перевод и адаптацию работ Кантора на французский язык, Пуанкаре получал шпильки в свой адрес со стороны Рассела и Цермело, которые называли его ретроградом, игнорирующим новый математический метод. Но и Пуанкаре немолчал, насмехаясь над логицистским течением: «Логика не стерильна, она порождает противоречия». Кроме того, он указывал на то, что если бы всю математику можно было вывести на одних только правилах логики, получилось бы, что математика была всего лишь гигантской тавтологией, логической истиной в стиле А = А. С его точки зрения, логика напоминала машину по производству сосисок: на входе помещают свинью, а на выходе получается вполне упорядоченная связка. Но математика работает не как пианола. Математическое доказательство представляло собой творческий механизм: благодаря интуиции мы способны доказать бесконечное число силлогизмов за конечное число шагов (принцип индукции). Именно этот переход от конечного к бесконечному определяет, по мнению Пуанкаре, чудо математики. Интуиция — это молния, которая освещает математику путь посреди ночи и позволяет ему изобретать математику. Посредством интуиции именно человеческий разум создает математические объекты.
Искусство математики заключается в том, чтобы найти этот особый случай, содержащий в себе все истоки обобщенности. Давид Гильберт
Брауэр перенял эту живописную философию математики Пуанкаре, с которым лично встретился в 1909 году. В противоположность платонизму и логицизму, утверждающим, что математические истины открываются сами, интуиционизм утверждает, что на самом деле они изобретаются (этот тезис сближает его с формализмом). Однако на вопрос, где находится математическая точность, интуиционизм Брауэра отвечает: «разум», а формализм Гильберта: «бумага». У Брауэра и Гильберта, которые познакомились во время отпуска в 1909 году, имелись две конфликтные темы: прежде всего это природа математики — как свободная конструкция человеческого понимания или как аксиоматическая теория — и роль принципа исключенного третьего в математике. Нерв интуиционизма именно в отрицании этого логического принципа, отсылающего к Аристотелю и утверждающего, что дизъюнкция пропозиции и ее отрицание — это логическая истина, то есть она всегда истинна, в любой модели или вселенной толкования (╞Av ¬A). Другими словами, либо А истинно, либо истинно отрицание А, потому что любой третий вариант систематически исключен (именно поэтому говорят об «исключенном третьем»). Наряду с принципом непротиворечия (╞¬(A^¬A)) и принципом идентичности (╞(перевернутое A)x(x = х)) этот принцип образовывал три классических закона рассуждения. Однако для Брауэра это необязательно было так. Поскольку мы не знаем, содержит ли десятичное продолжение числа π 20 нулей подряд, пропозиция «десятичное продолжение числа π содержит 20 нулей подряд» не является (и в этом ключ к интуиционизму) ни истинной, ни ложной. Ее истинность на сегодняшний день не может быть определена. Один единомышленник Брауэра утверждал, что принцип исключенного третьего для такого типа пропозиций может быть справедливым для Бога (Он знает всю бесконечную последовательность знаков после запятой такой, как она есть), но такое невозможно для человеческой логики. Совершив разворот на 180° по отношению к логистической догме, интуиционисты считали такую логику ответвлением математики, а не наоборот. Этот образ мысли положил начало тому, что с тех пор известно как «интуиционистская логика», формализованная прилежным учеником Брауэра Арендом Гейтингом (1898— 1980). В классической логике двойное отрицание пропозиции равносильно пропозиции, то есть ¬¬А↔А. Но интуиционистская логика отрицает, что из двойного отрицания пропозиции можно вывести исходную пропозицию. Следовательно, ¬¬А→А не принимается. Этот интуиционистский пересмотр классической логики отвечает на вопрос: почему Брауэр отвергал рассуждения доведением до абсурда (к которым нередко прибегал Гильберт)? Доказательством ложности отрицания А не доказывалось, что А истинно, поскольку был оставлен принцип исключенного третьего. Нидерландский математик считал справедливыми только конструктивные доказательства. Доказать, что отрицание теоремы противоречиво, — неравносильно доказательству, что теорема истинна, поскольку, прежде чем доказать последнее, нужно открыто сконструировать ее содержание. Для математиков-интуиционистов неконструктивные доказательства существования (доведением до абсурда) свидетельствуют о том, что в мире есть скрытое сокровище, но не указывают его местонахождение, поэтому такие доказательства имеют исключительно эвристическую ценность. Для существования математического объекта недостаточно, чтобы он не порождал никакого противоречия; нужно ввести эффективную процедуру его построения. Парадоксы, открытые в рамках теории множеств, по мнению Брауэра, явно представляли собой опасность для чисто экзистенциальной математики. Не зря Кронекер всегда ожесточенно спорил с Кантором о том, что если не построить множества, о которых тот говорил (а он не мог их построить, поскольку подавляющее большинство их было бесконечным), теоремы теории множеств растворятся в воздухе. Нужно было вернуться на путь греческой математики, которая была конструктивной, а значит интуиционистской, при этом бесконечность присутствовала только в потенции, но никогда не была актуальной. Гаусс уже высказывал подобное мнение: «Я прежде всего протестую против применения бесконечной величины как завершенной, в математике это никак не допустимо. Понятие бесконечности есть лишь способ выражения понятия предела». Для интуиционистов все трудности оснований математики исходили из использования бесконечности как чего-то законченного и идеального. Это нарушение происходит при попытке определить реальное число, такое, например, как число π = 3, 141592... Это многоточие после первых знаков после запятой создает у нас ложное ощущение, будто перед нами закрытый объект. В итоге речь зашла о восстановлении классической математики, насколько это возможно, без обращения к принципу исключенного третьего и к доведению до абсурда. В 1918 году Брауэр начал реализацию своего плана, который он назвал «вторым актом интуиционизма» («первый» акт предполагался как интуитивное основание математики), в статье «Основание теории множеств, независимо от принципа исключенного третьего». Держась за интуиционизм Канта, Брауэр основывался на временной перечислимости и признавал возможность только счетных множеств, считая несчетные множества противоречащими интуиции. Как говорил Кронекер, «Бог создал натуральные числа, все остальное создано человеком». С несчетными множествами работать нельзя, чтобы не столкнуться с серьезными парадоксами. В интуиционистской теории множеств сами множества получают имя видов, и единственные позволенные собрания чисел — конечные собрания: {0}, {0, 1}, {0, 1, 2}... Ни в коем случае не разрешено внезапно образовывать ансамбли из всех натуральных чисел {0, 1, 2,...}. Следовательно, алефы Кантора исчезают в тумане.
Бесконечность! Ни один другой вопрос так не вдохновлял человека, ни одна другая идея так не стимулировала его интеллект, ни одно другое понятие не требует большего разъяснения. Давид Гильберт
Аренд Гейтинг, в свою очередь, вплотную подошел к арифметике. Интуиционистская арифметика включает в себя те же математические законы, что и классическая, но она подчиняется только логическим законам, которые удовлетворяют интуиционистов. В отличие от интуиционистской теории множеств, которая жертвовала значительной частью классической теории множеств, интуиционистская арифметика приготовила сюрприз: тесную связь с классической арифметикой. В 1933 году Курт Гёдель доказал, что для каждой формулы, доказуемой в арифметике Пеано, существует равносильная формула, которая доказуема в арифметике Рейтинга, и наоборот. Интуиционистская арифметика только внешне была слабее классической. Наконец, в своей работе «Континуум» (1918) Герман Вейль попытался восстановить анализ с интуиционистских позиций. Он отказывался принимать произвольные множества натуральных чисел, учитывая только те бесконечные множества, которые можно было определить, построить. Поэтому ему удалось определить только те действительные числа, которые соответствуют арифметическому закону. То есть он восстановил только счетное количество несчетных чисел, которые составляют континуум. Для классического математика числовая прямая содержит все возможные последовательности Коши или сечения Дедекинда, а не только те, которые определимы, то есть те, которые можно уточнить с помощью построительного правила. И поскольку они представляют собой счетное количество, то оставляют числовую прямую полной отверстий, — это атомизированный континуум. Из чего следует, что интуиционистский анализ чрезвычайно отличается от классического. Математики-интуиционисты не принимают, например, теорему Больцано. И наоборот, классические математики не принимают многих результатов интуиционистов (для интуиционистов, например, не существует разрывных функций). Интуиционистская реконструкция логики и математики не очень-то вдохновляла, хотя имела широкое распространение. Это была не реконструкция, а скорее разрушение. Интуиционистская математика искалечила классическую математику.
 Снимок с торжества по случаю 60-летия Давида Гильберта. Рядом с ним вдова его друга Минковского (справа) и его жена Кёте. В тот период он полностью отдался спору с интуиционистами об основаниях математики.
Снимок с торжества по случаю 60-летия Давида Гильберта. Рядом с ним вдова его друга Минковского (справа) и его жена Кёте. В тот период он полностью отдался спору с интуиционистами об основаниях математики.
 Гильберт в своем саду вместе с Германом Вейлем, одним из своих любимых учеников, который, однако, выступал на стороне интуиционистов.
Гильберт в своем саду вместе с Германом Вейлем, одним из своих любимых учеников, который, однако, выступал на стороне интуиционистов.
 Ян Брауэр, нидерландский математик, который возглавил интуиционистское движение, считая своими предшественниками Канта, Кронекера и Пуанкаре. Самый ярый противник Гильберта.
Ян Брауэр, нидерландский математик, который возглавил интуиционистское движение, считая своими предшественниками Канта, Кронекера и Пуанкаре. Самый ярый противник Гильберта.
Интуиционизм с его постоянным воззванием к конструктивности, основанной на временной перечислимости и на отказе от принципа «третьего не дано», выбросил за борт более половины классических достижений. С Брауэром математика обрела ясность, но математики наблюдали, как передовые теории, которые казались им прочными как скалы, обращаются в пепел. Хотя нидерландский математик без колебаний принял разрушение анализа, большая часть математического сообщества сочла это неприемлемым. Некоторые математики заговорили о «большевистской угрозе», которую несет Брауэр. И тут Гильберту пришлось вмешаться.
«ЖРЕБИЙ БРОШЕН»
Полемика между формализмом и интуиционизмом лежала в основе всего спора об основаниях в 1920 годы, при этом Гильберт и Брауэр были ее главными участниками. Спор, то ли из-за сложного характера Брауэра, то ли из-за большого авторитета Гильберта, перешел чисто академические границы и обрел форму личного противостояния. Началось оно в 1921 году, и сразу потеря в лагере Гильберта: дезертировал его блестящий ученик Герман Вейль. В этом году он опубликовал памфлет «О новом кризисе оснований математики», в котором поддерживал разгромные тезисы Брауэра и называл себя апостолом интуиционизма, предсказывая приход математической революции. Спор затрагивал важнейшие стороны концепции математики Гильберта, но его бурная реакция отчасти объяснялась вопросами репутации. Если самый выдающийся ученик перешел в стан врага, почему этого не смогут сделать остальные? В счастливые 1920-е, которые совпали с последним исследовательским этапом в его карьере, уже пожилой Гильберт посвятил себя спору об основаниях математики. И он вмешался в него со всем пылом, что определило в споре действительно новый поворот. Немец предложил «программу Гильберта» (уже намеченную в его знаменитой лекции в Париже в 1900 году), чтобы раз и навсегда заложить основы математики. Для Гильберта наука была организмом, который растет и развивается одновременно во многих направлениях. Прояснение оснований с помощью аксиоматического метода было одной из фаз этого роста, и несмотря на всю важность, она необязательно была приоритетной. Для описания этой концепции Гильберт использовал характерную для себя метафору: «Здание науки строится не как дом, где сначала закладывают прочный фундамент, а потом уже переходят к сооружению конструкции и отделке комнат. Наука прежде всего охватывает широкое пространство, чтобы иметь возможность свободно развиваться. И только после того, как проявляются первые признаки того, что ее слабый фундамент не выдерживает, принимаются за его укрепление и переопределение. Это признак не слабости науки, а наоборот. Это правильный и здоровый путь ее развития». В математике время исследования оснований уже пришло. С 1900 года убежденный в надежности аксиоматического метода, который так хорошо себя показал в геометрии, Гильберт навязывал аксиоматический подход остальным математическим дисциплинам, в частности теории множеств, а также сделал первые шаги для основания математической теории доказательства. Пока платонизм и логицизм утверждали, что точностью математики ведает царствие небесное, а интуиционизм приписывал это человеческому разуму, формализм Гильберта связывал ее с исписанным листом бумаги. Математику можно рассматривать как игру знаков, лишенных значения, как цепь символов на бумаге, свободных от смысла, но подчиняющихся некоторым правилам, чтобы с ними можно было работать. Формалистская позиция, которую развили Гильберт и его соратники (Бернайс и Аккерман), предлагала решение, основанное на двух моментах: во-первых, на общей аксиоматизации математики и логики, а во-вторых, на доказательстве непротиворечивости этой формальной системы. Доказательство, что внутри системы нельзя вывести никакого противоречия, было краеугольным камнем формалистского здания. Однако сперва требовалось дать отпор набравшему силу интуиционизму европейских математиков. После Первой мировой войны критика классической математики, сформулированная Брауэром и Вейлем, усилилась и побудила Гильберта попытаться искоренить все скептические сомнения. Гильберт осознавал, что позиция Брауэра и Вейля не лишена обоснования и нужно действовать осторожно, чтобы не спровоцировать парадоксы теории множеств. Но он не был готов отказаться ни от теории Кантора (не зря первой проблемой в списке 1900 года была его континуум-гипотеза), ни от достижений классической математики (включая достижения, полученные с использованием самой многострадальной аксиомы, аксиомы выбора). Значительная часть его успеха как математика обязана доказательствам существования, как раз против таких доказательств Брауэр (как до него Кронекер и Гордан) и выступал. Пытаясь пресечь его влияние, Гильберт задался вопросом, что можно сделать, чтобы не отказываться от принципа исключенного третьего. По его мнению, отнять этот принцип у математика было равносильно тому, чтобы запретить астроному использовать телескоп или боксеру пускать в ход кулаки. Профессор из Гёттингена был удивлен и разочарован тем, что целый круг математиков, не церемонясь, заняли сторону противника, и это серьезно сказалось на математике. Континуум или трансфинитные числа Кантора оказались в положении обреченных математических объектов. А теорема, доказывающая существование бесконечного количества простых чисел, в свою очередь, была ярким примером запрещенного образа мысли. Действительно, принятие идеи, что любая значимая пропозиция либо истинна, либо ложна, является основополагающим для метода косвенного доказательства. Евклид доказал существование бесконечного количества простых чисел, продемонстрировав, что противоположный тезис является ложным, то есть воспользовавшись принципом исключенного третьего. Поскольку его доказательство не было конструктивным и не позволяло определить и-ное простое число, оно не годилось для интуиционистов. По сравнению с классической интуиционистская математика предполагала жалкий остаток, ряд изолированных и бессвязных результатов. Постоянный страх Гильберта был вызван тем, что интуиционизму удастся расчленить математику и при этом будут утрачены ценные достижения. Он был насколько удручен этим положением вещей, что, борясь с интуиционизмом, даже переходил на личности и оперировал не совсем академическими аргументами: «Программа Брауэра — это не революция, а банальное повторение старых методов [отсылка к Кронекеру] бесплодного поиска, который, даже если применить его с удвоенной силой, полностью проваливается. Сегодня мы вооружены благодаря работам Фреге, Дедекинда и Кантора. Попытки Брауэра и Вейля заранее обречены на поражение». В конце десятилетия, когда борьба между двумя группами достигла апогея, Гильберт почувствовал, что силы на исходе и злокачественная анемия убивает его. И тогда он испугался, что после его смерти Брауэр обретет могущество и склонит к интуиционизму журнал Mathematische Annalen, который Гильберт возглавлял. В итоге в 1928 году он совершил немного грязный маневр и исключил Брауэра из редколлегии. Несмотря на возражения Эйнштейна, большинство ученых прислушались к воле Гильберта, и Брауэру пришлось уйти. Это столкновение надломило нидерландского математика, и он более чем когда-либо ударился в солипсизм. Гильберт назвал этот эпизод «войной мышей и лягушек». Гильберт выиграл битву, но не войну.ГЛАВА 5 Крах программы Гильберта
Гильберт мечтал поместить математику на аксиоматический фундамент. К сожалению, теоремы Гёделя не позволили его мечтам стать явью. В математике, задуманной как формальная система, всегда останется место гипотезе, истинность или ложность которой нельзя доказать. Еще хуже — никогда нельзя будет доказать, что она лишена противоречий. Когда возведение здания математики уже завершалось, его фундамент вновь разрушился. К концу 1920-х годов ангел формализма и демон интуиционизма все еще боролись за душу каждого математика. Но, к удовольствию Гильберта, формализм мчался на всех парусах. Казалось, «программа Гильберта» вот-вот свершится. Никто, даже самые реакционно и революционно настроенные математики, не могли изгнать формалистов из фантасмагорического собора, выстроенного из бесконечностей Кантора. Никто не мог заставить их перестать слушать симфонию бесконечности — классического анализа. После 1900 года, когда Гильберт прочитал ту знаменитую лекцию в Париже, на III Международном конгрессе математиков 1904 года, проведенном в Гейдельберге, он представил свою точку зрения на кризис оснований, но в течение следующих 15 лет больше не возвращался к этой теме — анализ и физика полностью захватили его. Движимый желанием дать отпор интуиционистам, он снова обратился к теме основ математики сначала в 1917 году, а затем постоянно возвращался к ней с 1922 года. Для Гильберта и формалистской школы объекты математической мысли — это символы сами по себе, и фундаментальная проблема — это проблема устойчивости или непротиворечивости математики. Чтобы окончательно обосновать математику, он не нуждался ни в Боге, как Кронекер, ни в предположении об особенностях нашего восприятия в соответствии с принципом индукции, как Пуанкаре, ни в оригинальной интуиции, как Брауэр, ни даже в аксиоме о бесконечности или аксиоме о редуктивности, как Рассел и Уайтхед. Как таковая проблема оснований математики должна была окончательно устраниться после проверки на непротиворечивость аксиоматической системы математики.СИЛЬНЫЕ СТОРОНЫ ПРОГРАММЫ
Несложно проследить происхождение идей Гильберта. В 1900 году он опубликовал лекцию «Понятие числа», прочитанную годом ранее на ежегодной ассамблее Немецкого математического общества. После книги об основаниях геометрии эта работа стала его второй публикацией, касающейся аксиоматического метода. В ней он рассматривал два возможных подхода к математическим понятиям — генетический и аксиоматический. Классический пример применения генетического метода характерен для арифметики. Натуральные числа появляются на основе базовой интуиции счета: если требуется произвести вычитание любых натуральных чисел, система расширяется, чтобы включить в себя целые числа. Необходимость разделить два любых целых числа приводит к введению рациональных чисел, а чтобы иметь возможность извлекать корни, добавляются иррациональные числа и дается определение действительным числам. Гильберт отмечал, есть аксиоматический метод, типичный для геометрии (и для анализа, поскольку Гильберт показал, как аксиоматизировать действительные числа). Несмотря на высокую дидактическую ценность генетического метода, аксиоматический метод имеет преимущество обеспечения полной логической надежности. В этой ранней работе Гильберт открыто и впервые заявил о необходимости подхода к проблеме абсолютной непротиворечивости арифметики как к унаследованной от геометрии (относительную непротиворечивость которой он сам доказал). Этот вопрос занял второе место (ему предшествует только континуумгипотеза) в списке из 23 открытых проблем 1900 года; Гильберт вернулся к нему на конгрессе 1904 года, хотя и недооценил его сложность. Задача заключалась не в том, чтобы найти самые базовые модели, на которые можно было бы опереться, чтобы вывести непротиворечивость арифметики, как это было сделано с аксиомами геометрии (при этом была бы доказана только относительная непротиворечивость). Следовало разработать доказательство абсолютной непротиворечивости, основываясь на синтаксисе, а не на семантике, то есть выяснив, позволяет формальная система, выражающая арифметику, прийти к противоречиям или нет. Однако только около 1904 года, когда стали проявляться парадоксы, Гильберт убедился, что основные усилия необходимо направить на аксиоматический анализ как часть более обширной задачи — установления непротиворечивости арифметики (поскольку и геометрия, и анализ были сведены к ней). Как обычно, Гильберт выбрал себе соратника — на этот раз Цермело — и поручил ему детальную разработку аксиоматизации теории множеств. Именно так начали вырисовываться два основных момента программы Гильберта: сперва аксиоматизация, затем непротиворечивость. На первом этапе было необходимо формализовать теорию множеств, а также логику и арифметику. Наивные определения не позволяли вывести строгие рассуждения, лишенные парадоксов. Следовало полностью формализовать известную математику, переведя все ее содержимое в формальную систему, выраженную с помощью нового символического языка: 0 (число нуль), s (функция последующего члена), ¬ (не), v (или), ^ (и), →(вывод), Ǝ (квантор существования), перевернутое А(квантор всеобщности), = (равенство), х (переменная) и так далее. Как раз в 1928 году, спустя 50 лет после первого шага Фреге, Гильберт и Аккерман опубликовали «Основы теоретической логики» — учебник по дисциплине, сегодня называемой логикой первого порядка. Их формализация достигла канонического уровня, и сегодня она известна как система Гильберта — Аккермана. Они установили формальный синтаксис, а также предложили аксиомы и правила этой логики, что позволяет выводить новые формулы. Логика первого порядка превратилась в настоящее исчисление.Вначале был знак. Давид Гильберт, «Новые основания математики» (1922)
В учебнике Гильберта и Аккермана были сформулированы некоторые металогические вопросы о свойствах исчисления, ими разработанного. Они перекликались, в частности, с доказательством (в 1926 году предложенным Бернайсом) того, что элементарная логика, или логика пропозиций, является верной (любая доказуемая формула верна) и полной (любая логическая истина, в свою очередь, доказуема), и к этому же результату в 1922 году независимо пришел Эмиль Пост (1897- 1954). Авторы задавались вопросом — является ли таковой логика первого порядка? — хотя признавали, что ответ не найден. Ровно через год, в 1929 году, молодой австрийский логик Курт Гёдель доказал полноту логики первого порядка в своей докторской диссертации, написанной под руководством Ханса Хана (1879-1934), хотя опубликовал ее он лишь в 1930 году Эта логика была верной (все доказуемые формулы истинны) и полной (все логические истины, все тавтологии доказуемы). При исчислении предикатов первого порядка синтаксическое понятие дедукции и семантическое понятие истины совпадают, имеют одно и то же расширение. Программа Гильберта неожиданно обрела успех: любая логически справедливая формула, то есть истинная в любой возможной интерпретации, выводима с помощью описанных исчислений. Но что произойдет, если к этому чистому исчислению предикатов добавить аксиомы и правила, которые относились бы к арифметике или к теории множеств? Останется ли оно верным и непротиворечивым? И полным? На втором этапе в объект математического изучения следовало превратить само понятие доказательства, чтобы таким образом доказать непротиворечивость арифметики и искоренить все сомнения. В математике нет места полуправде. Для Гильберта математик занимается понятием математического доказательства, точно так же как физик проверяет работу своих приборов или философ критически осмысливает свои же аргументы. Разработка «теории доказательства» позволит рассматривать доказательства в качестве результата чистых сочетаний символов, согласно предписанным формальным правилам. В этих условиях было достаточно доказать, что никакое формальное выведение, никакое сочетание символов не может привести к формуле 0≠0 (что является противоречием). Так была бы установлена непротиворечивость арифметики. Достаточно доказать, что есть одна недоказуемая формула, поскольку если бы все формулы были доказуемы, мы могли бы вывести противоречие (доказав пропозицию и обратную ей), и система оказалась бы противоречивой. И наоборот, если бы система была противоречивой, поскольку из противоречия следует что угодно (ex contradictione sequitur quodlibet, как уверяли схоластики), мы могли бы доказать любую формулу (формула «если 0≠0, то Р» всегда истинна, справедлива, поскольку таковой не является предпосылка). В 1920 годы Гильберт ввел идею о том, что его «теория доказательства» подходит к вопросу непротиворечивости на двух уровнях рассмотрения. С одной стороны, это математический уровень, как представлено в рамках формальной системы. С другой стороны, это метаматематический, дискурсивный уровень, на котором говорится об аксиоматизированной математике. На данном уровне следовало доказать непротиворечивость посредством ряда техник, которые изучали бы формальную систему извне, отключив ее от любого числового значения или значения, связанного с бесконечностью, просто в качестве конечных цепочек первичных знаков, на основе которых можно образовать формулы и доказательства в соответствии с некоторыми предопределенными правилами. Пропозиции, которые относятся к этому формальному скелету, к этой арифметике, лишенной значения, — это метаматематические пропозиции, которые формулируются не на языке объекта, а на метаязыке. Это как если бы на уроке английского использовался испанский язык, чтобы показать оттенки какого-нибудь англосаксонского слова. Вопрос о непротиворечивости в математике или вопрос, является ли формула 0≠0 доказуемой, — по сути, то же самое, что спрашивать, является ли определенная шахматная позиция правомерной, то есть можно ли достичь ее из исходного положения партии и по правилам передвижения фигур. Чтобы на него ответить, мы не играем в шахматы, а размышляем о собственно шахматах.
Сомневайся в данных, пока данные не оставят места сомнению. Анри Пуанкаре
Но Гильберт настаивал на том, что математическое доказательство непротиворечивости арифметики должно удовлетворить как классических математиков, так и интуиционистов, то есть оно должно проводиться финитными, конструктивными методами, которые не требуют вмешательства бесконечности. В конце жизни Пуанкаре подчеркивал, что если для доказательства непротиворечивости арифметики — даже в математическом плане — воспользоваться принципом индукции, то есть пятой аксиомой Пеано, получится порочный круг: попытка доказать связность арифметики с помощью арифметического принципа. Нужно было доказать это посредством самоочевидных рассуждений, что сами математические методы, даже когда они предполагают присутствие актуальной бесконечности, справедливы, то есть не позволяют вывести противоречие. Более того, Гильберт хотел доказать не только непротиворечивость математики, но также ее полноту. Это был другой нерешенный вопрос из его лекции 1900 года: возможность решения любого математического вопроса. Гильберту и его соратникам удалось доказать непротиворечивость некоторых простых формальных систем. Так, в 1922 году Гильберт сконцентрировался на элементарной части арифметики и, изучая вид доказуемых формул, сделал вывод, что формула 0≠0 — не из их числа. Это доказательство позже было развито Аккерманом в его докторской диссертации (датированной 1925 годом и написанной под руководством Гильберта), а также в 1927 году элегантно упрощено фон Нейманом. Но это были фрагментарные достижения: формальные арифметические системы, из которых следовала непротиворечивость, не включали в себя принцип индукции. В 1929 году польскому математику Мойжешу Пресбургеру (1904-1943) удалось доказать непротиворечивость арифметики, включающей в себя принцип индукции и сложение, но не умножение. Эти результаты обрели форму двухтомника, написанного Бернайсом от лица Гильберта и озаглавленного «Основания математики» (1934-1939). Однако непротиворечивость систем, описывающих достаточно большую область арифметики с натуральными числами, все еще оставалась неохваченной.
ГЁДЕЛЬ: БУРИ И ШКВАЛЫ
К 1930 году первый пункт программы Гильберта в целом был выполнен: логика, теория множеств и арифметика аксиоматизированы. Но все еще оставался вопрос об их непротиворечивости и полноте. Гильберт вышел на пенсию, когда ему исполнилось 68 лет. В связи с получением звания почетного гражданина Кёнигсберга заслуженный профессор Гёттингенского университета произнес речь в своем родном городе. В ней он вновь отстаивал идею, что в математике нет неразрешимых проблем. Записывая обращение для местного радио, он четко произнес последнюю фразу своей речи: «Мы должны знать. Мы будем знать» и улыбнулся. Запись сохранилась, и если прислушаться, в конце можно уловить смех Гильберта. Это было 8 сентября 1930 года. По иронии судьбы, за три дня до этого в Кёнигсберге состоялась конференция по эпистемологии точных наук. Цель встречи состояла в том, чтобы определить, на какой стадии находится разрешение кризиса оснований математики. Выступали представители каждого из связанных с основаниями течений. От логицизма — Рудольф Карнап (1891-1970), изложивший концепцию математики, которую сформулировал в Венском кружке: математические теоремы как тавтологии, логические истины. От интуиционизма — Аренд Гейтинг, выступавший за исключение бесконечности из математики. И от формализма — Джон фон Нейман, сторонник Гильберта. А 6 сентября слово взял 24-летний австрийский логик Курт Гёдель и доложил о недавно полученных им результатах: «Я могу привести примеры истинных арифметических пропозиций, недоказуемых в формальной системе классической математики». Несмотря на важность этого заявления, оно осталось незамеченным. И только фон Нейман был в недоумении. Несмотря на то что он всегда мечтал доказать непротиворечивость всей математики посредством финитных методов, в его голову уже закралось сомнение, что на самом деле это невозможно, и краткое выступление застенчивого юноши в круглых очках показалось его событием невероятного значения. Это был смертный приговор красивому девизу Гильберта. Надежда, которая теплилась в душе немецкого математика более 30 лет, должна была окончательно угаснуть. Математика больше никогда не будет надежной. Когда в 1931 году были опубликованы теоремы Гёделя о неполноте, в программе Гильберта произошло короткое замыкание. Чтобы объяснить, почему это произошло, нам нужно обратиться к математической логике. С эпохи Аристотеля, не забывая о вкладе схоластиков, логика задумывалась как учение о рассуждении, которое никогда не происходит в пустоте, а всегда в рамках какого-то языка. С течением времени математики обращали все большее внимание на логику языков, на которых они изъясняются, чтобы определить их возможности. Логика научила математиков тому, что в языке существует два основных понятия: одно — семантического характера, понятие истины, другое — синтаксического характера, понятие доказательства. Сложность заключалась в том, чтобы определить радиус их действия: совпадают ли эти два понятия экстенсионально, пусть они сильно различаются интенсионально. Другими словами, является ли все доказуемое истинным (правильность) и все истинное — доказуемым {полнота). В целом языку, богатому в плане выражения, соответствует логика, бедная на интересные свойства. Так, логика языков первого порядка является правильной и полной, но математику ее обычно не хватает в ежедневной работе (когда нужно количественно оценить свойства, а не только объекты). Но не следует ожидать, что логика языков второго порядка или выше будет полной. Так что одно из двух: либо мы занимаемся математикой на маловыразительном языке, логика которого правильна и полна, либо мы формализуем наши математические рассуждения на выразительном языке, но логика, лежащая в его основании, в лучшем случае правильна (мы можем доказывать лишь истины), но не полна (мы не можем доказать все истины).Гёдель — величайший логик со времен Аристотеля. Джон фон Нейман о Гёделе
Ограничиваясь языком первого порядка (где можно давать количественную оценку только объектам), если мы будем толковать объекты как числа, мы едва ли уйдем дальше элементарной арифметики (например, теорема, утверждающая, что любое множество натуральных чисел обладает минимальным невыразимым элементом, поскольку нам придется давать количественную оценку множествам чисел) и никогда не доберемся до анализа. Проблема в том, что функции или числовые отношения не являются числами. Однако эта трудность испаряется, если мы рассматриваем множества, поскольку функции и отношения между множествами — это, в свою очередь, другие множества: я-ные собрания множеств — это множества. Возникает важный вопрос: можно ли свести всю математику к теории множеств? Если истолковать объекты нашего языка первого порядка как множества, легко эмпирически убедиться, что большинство математических сущностей можно определить на основе множеств. Эта программа исследования основывалась на вышеупомянутой теории множеств ZF: на базе небольшого количества аксиом, сформулированных в первом порядке, эта теория множеств была способна охватить значительную часть математики того времени. Снова, как в итоге понял Гёдель, цена этого теоретического богатства (выразимость) — метатеоретическая бедность, которая проявляется в нескольких ограничивающих результатах: теоремах о неполноте. В первой теореме доказывается, что существует истинная формула, которая недоказуема в ZF (хотя в работе Гёделя в качестве отправной формальной системы взят труд Рппсгрга mathematica, а его результаты справедливы для ZFи других смежных систем). А во второй — что невозможно доказать непротиворечивость ZF в ZF. Более того, доказательство в ZF отсутствия противоречия в ZF и, следовательно, в математике доказало бы исключительно, что ZF и математика противоречивы. Гёдель положил конец надежде на формализм Гильберта. Все усилия, направленные на доказательство непротиворечивости математики, обречены на провал. Точнее, невозможно доказать посредством финитных методов отсутствие противоречий любой формальной системы, содержащей арифметику Пеано (если позволить себе применение тяжелой артиллерии, непротиворечивость все-таки возможно доказать, как в 1936 году это сделал ученик Гильберта Герхард Генцен (1909-1945), хотя и посредством трансфинитных методов, очевидность которых спорная).
Кто из нас не возликовал бы, подними он занавес, за которым скрывается будущее, загляни он в последующие достижения науки и секреты ее развития?! Давид Гильберт, из речи на II Международном конгрессе математиков в Париже
Парадокс лжеца был для Гёделя одним из двигателей доказательства теорем о неполноте. Поскольку доказательство было на грани перехода в цикличность, некоторые математики — в частности, 60-летний Цермело — не осознали его ценности. Гёдель придумал ловкий перевод на метаязык внутри языка: арифметизацию метаматематики. С помощью смелой цифровой кодификации, основанной на простых числах (которую с тех пор называют гёделизацией), он назначил номера знакам так, чтобы с каждой формулой (и также с каждым доказательством) можно было связать число, кодировавшее бы всю структуру. Пропозиции, в которых говорилось о свойствах формальной системы, выражались в рамках системы посредством арифметических формул. Доказуемость, например, была представлена в виде числового отношения. В таких условиях Гёдель вышел из ситуации, составив формулу G, которая говорит сама о себе: «я недоказуемо». Эта формула стала примером неразрешимого утверждения внутри формальной системы: ни она, ни ее отрицание не являются теоремами, то есть чем-то доказуемым. Действительно, Іеделю удалось доказать, что G доказуемо тогда и только тогда, когда ¬G доказуемо. Следовательно, если мы хотим, чтобы формальная система была непротиворечивой, ни G, ни ¬G не могут быть таковыми. Если бы G было доказуемо, так как ¬G утверждает в метаматематических терминах, что G доказуемо (отрицает то, что оно недоказуемо, как сказано в нем самом), то было бы возможно доказать также ¬G и вывести противоречие (G^¬G). И наоборот, если бы ¬G было доказуемым, мы могли бы по той же причине доказать G и прийти к тому же противоречию. В итоге доказательство любой из этих двух формул автоматически предполагало бы противоречивость системы. Более того, если допустить, что формальная система непротиворечива, то G недоказуемо, но истинно. Если бы G было ложно, так как в G говорится: «я недоказуемо», то G было бы доказуемо, что невозможно. Следовательно, у нас есть высказывание G, которое, хотя и недоказуемо, является истинным. Существование неразрешимого утверждения предполагает, что аксиомы теории не содержат ответа на все вопросы, формулируемые формальным языком, потому что ни утверждение, ни его отрицание не являются теоремами. И так как либо оно, либо его отрицание должно быть истинным, у нас есть истинная недоказуемая формула. Хуже всего, что если добавить неразрешимое утверждение в качестве аксиомы, появляются другие, новые. Математика вдруг очнулась от гильбертова сна — от мечты о полноте, в которой аксиоматические системы не содержат неразрешимых формул, а истинное всегда совпадает с доказуемым. Проще говоря, «непротиворечивый» предполагает «неполный», и наоборот, «полный» предполагает «противоречивый». Ни одна формальная система, содержащая привычную арифметику, не может быть одновременно и той и другой. Если мы предположим, что она непротиворечива, она всегда будет неполной, то есть будет содержать недоказуемые истины. Будут существовать некоторые истинные свойства формально неразрешимых чисел, то есть свойства, которые мы не можем ни доказать, ни отвергнуть на основе аксиом. Но за первой теоремой о неполноте следует вторая: так как непротиворечивость равносильна утверждению, что формула 0≠0 недоказуема, Гёдель трансформировал это последнее математическое свойство в арифметическую формулу (назовем ее С) и заметил, что в первой теореме установлено, по сути, что «C→G». Непротиворечивость предполагает, что существует неразрешимое утверждение и, следовательно, неполнота. Так что доказательство С позволило бы нам исключить G из импликации «C→G» посредством modus ponens и, следовательно, доказать G, что невозможно, поскольку G недоказуемо. Это удивительное следствие сводится к тому, что непротиворечивость формальной системы, которая включает в себя арифметику, недоказуема в рамках формальной системы. Гёдель не доказал должным образом эту вторую теорему, он только высказался о ее приемлемости, но так никогда и не записал обещанного доказательства. Первое полное доказательство, очень тщательное, появилось, что любопытно, в 1939 году, во втором томе «Оснований математики» Бернайса и Гильберта. Мало того, к синтаксическим ограничениям, которые открыл Гёдель, присоединилось другое ограничение — семантическое, формальных систем первого порядка: теорема, сформулированная Леопольдом Лёвенгеймом (1878-1957) и Туральфом Скулемом (1887-1963) около 1920 года (Скулем вернулся к ней в 1933 году). В 1930 году в рамках своего доказательства полноты логики первого порядка Гёдель мимоходом доказал, что любая непротиворечивая теория первого порядка имеет модель, в которой аксиомы проверяются, хотя и ничего не добавил о том, какие характеристики имеет эта модель и как ее построить. Лёвенгейм и Скулем до этого заметили, что любая непротиворечивая формальная система первого порядка имеет, по сути, счетную модель. Это порождает парадокс Скулема: если ZF непротиворечиво, то оно обладает счетной моделью. То есть несчетный континуум, которым мы намереваемся оперировать в ZF, может относиться к счетному множеству вне ZF. Теория действительных чисел, от которой мы ждем знакомой несчетной модели («настоящие» действительные числа), также имеет счетную модель.
ТЕОРЕМА ТАРСКОГО О НЕВЫРАЗИМОСТИ ИСТИНЫ
Альфред Тарский (1902-1993) считал себя лучшим из живущих математических логиков с ясным умом (чтобы избежать сравнения с Гёделем, страдавшим маниями и навязчивыми идеями). В 1939 году этому польскому ученому удалось переехать в США и на несколько десятилетий превратить университет Беркли в мировую столицу математической логики. Он любил работать ночью и увлекался психотропными средствами, которые помогали ему бодрствовать и трудиться без устали, а также имел репутацию Казановы. Тарский знаменит тем, что в 1933 году опубликовал огромную статью, в которой дал формальное определение истине и таким образом обозначил начало теории моделей. Если Гильберт в своей теории доказательства прояснил синтаксическое понятие формального доказательства, Тарский сделал то же самое с семантическим понятием истины. Альфред Тарский, 1968 год.
Альфред Тарский, 1968 год.
Еще одна ограничительная теорема
В 1933 году,через два года, после того как Гёдель объявил о двух результатах о неполноте, Тарский извлек на свет другую ограничительную теорему, хотя она уже была провозглашена и доказана Гёделем в письме Цермело, датированном 1931 годом. В этой ограничительной теореме установлено, что любая формальная теория первого порядка, содержащая базовую арифметику, неспособна (если она непротиворечива) выразить свое собственное понятие истины. Интересные непротиворечивые теории не могут содержать выражения «быть истинным» в своем языке, поскольку в этом случае они породили бы парадокс лжеца. С помощью гёделизации можно воспроизвести формулу Г, которая утверждает о самой себе, что она ложная. Воспользовавшись выражением «быть истинным», которое, предположительно, существует в языке, мы придем к следующему противоречию: Т истинное тогда и только тогда, если оно ложное, поскольку именно это утверждает Т. Как в случае с лжецом: я говорю правду, если я лгу. Без сомнения, математические логики сумели применить цикличность, лежащую в основе парадоксов, с большой пользой.ENTSCHEIDUNGSPROBLEM, ИЛИ ПРОБЛЕМА РАЗРЕШЕНИЯ
На IX Международном конгрессе математиков, проходившем в 1928 году в Болонье, Гильберт воспользовался случаем, чтобы предложить свой план по спасению математики и обозначить следующий вопрос: существует ли механическая процедура, которая решала бы все и каждую проблему математики, алгоритм, способный принципиально разрешить все математические вопросы, который при заданной математической пропозиции дал бы нам знать, является она теоремой или нет? Другими словами, является ли она разрешимой в математике? Как и на вопросы непротиворечивости и полноты, ответ на нее был отрицательным. После теорем Гёделя стало ясно, что ответ на эту проблему — категорическое «нет», поскольку математика является неполной: предполагаемый алгоритм в течение бесконечного времени «думал» бы над неразрешимым высказыванием, поскольку ни оно, ни его отрицание не являются теоремой. Следовательно, ответ на проблему разрешения оставалось дать только для логики первого порядка, которая, напомним, является полной. Однако в 1936 году Алан Тьюринг (1912-1954) и независимо от него Алонзо Чёрч (1903-1995) доказали, что логика первого порядка также неразрешима.Тезис Чёрча — Тьюринга
Для начала Тьюринг сформулировал, что означает думать как машина, механически. Его первая победа заключалась в определении понятия вычислимой функции: это функция, которую способна вычислить машина Тьюринга — вид компьютера без ограничений в пространстве или времени. Одновременно, по другую сторону Атлантического океана, Чёрч пришел к аналогичным выводам, разработав формальную систему, которую назвал лямбда-исчислением. С тех пор под названием тезиса Чёрча — Тьюринга известен постулат, утверждающий, что любое альтернативное определение вычислимости равносильно определению, данному Тьюрингом в терминах его машин. Прибегнув к изобретательному варианту диагонального аргумента Кантора, Тьюринг доказал, что существует намного больше функций, чем машин Тьюринга. Другими словами, существуют невычислимые функции. Исчислимые функции, как и машины Тьюринга, имеются в счетном количестве, то есть они как иголки в стоге сена всех функций. Наконец, рассмотрев проблему остановки, он предложил отрицательный ответ на вопрос Гильберта — Entscheidungsproblem: если бы существовала эта процедура, она также была бы способна определить за конечное время, останавливается любая машина Тьюринга через конечное число шагов или входит в бесконечную петлю, когда на входе вводятся некоторые данные. Но последнее, как он доказал, невозможно. Не существует алгоритма, способного получить на входе логическое или математическое высказывание и выдать на выходе: «теорема» или «не теорема» (хотя свойство выводимости действительно разрешимо в ограниченной логике пропозиций). Сланцевая статуя и портрет Алана Тьюринга в музее Блетчли-Парка.
Сланцевая статуя и портрет Алана Тьюринга в музее Блетчли-Парка.
Это означает, что теории первого порядка не могут контролировать кардинальное число своих моделей. Так, например, если сформулировать аксиомы арифметики Пеано в логике второго порядка (неполной), то они категориальны (то есть все их возможные модели изоморфны, имеют одно и то же кардинальное число), но если сформулировать их в логике первого порядка (полной), то мы расплачиваемся тем, что теряем категориальность. Появятся стандартная и нестандартная модели натуральных чисел. Скупость логика имеет свою цену. Вскоре Гёдель предположил, что континуум-гипотеза Кантора, которую в 1925 году Гильберт считал почти доказанной на основе выведенной из его теории доказательства изящной техники, была примером неразрешимого высказывания в привычной теории множеств. В 1938 году, ограничиваясь подмножеством конструктивных множеств, Гёдель доказал: невозможно доказать, что она ложная в ZFC. И обратно, в 1963 году Пол Коэн (1934-2007), использовав метод форсинга, доказал: также невозможно доказать, что она истина в ZFC. Гёдель и Коэн построили модели, в которых гипотеза истинна и ложна соответственно. Так что ни утверждение, ни отрицание континуум-гипотезы недоказуемо. То же самое происходит с аксиомой выбора, непротиворечивость и независимость которой относительно остальных аксиом также доказали оба математика. Следовательно, статус аксиомы выбора и континуум-гипотезы в теории множеств аналогичен статусу аксиомы параллельных прямых в геометрии. Рай Кантора — не единственный доступный рай теории множеств. Программа Гильберта выбыла с поля боя после двух ударов, полученных от Гёделя. Как первая, так и вторая проблемы знаменитого списка из 23 проблем Гильберта в итоге оказались решены, хотя и способом, который в 1900 году было трудно вообразить. В математике истинное не совпадает с доказуемым. Аксиом и правил выведения, которые Гильберт поставил во главу угла, было недостаточно, чтобы вывести все математические теоремы, при этом можно представить себе пропозиции истинные, но невыводимые в формальной системе классической математики. «Арифметика непротиворечива» — вот пример этого типа неразрешимых пропозиций. Гильберт, узнав о теоремах Гёделя спустя несколько дней (благодаря Бернайсу), попытался спасти часть своей программы, позволив использование нефинитных методов для доказательства непротиворечивости математики. Но эти методы совсем не очевидны. Гильберт и его команда походили на пастухов, которые построили убежище, чтобы защитить стадо от волков, но не могли быть уверены в том, что внутри нет ни одного волка.
БАЛАНС: ТРЕЩИНЫ ФОРМАЛИЗМА
Несмотря на то что скептические сомнения так и не были устранены, классическая математика все же чувствовала себя неплохо. Твердость и энтузиазм Гильберта смогли поддерживать курс большого корабля математики. С точки зрения обоснования математики формализм был отправлен в нокаут, но в отношении философии математики выиграли по очкам. Часто говорят, что платоническая позиция лучше всего характеризует отношение математика к сути этой дисциплины. Математик верит в реальность математических объектов. Но, конечно, когда философы начинают одолевать его своими вопросами, он бежит и прячется под юбкой формализма и заявляет: «Математика — всего лишь сочетание знаков, лишенных значения, красивая игра формул, еще интереснее, чем шахматы». Но при этом ее отношение к их реальному значению скрыто сумерками: если нужна точность, надо исключить любое значение; но если нужно, чтобы математика имела смысл, нужно отказаться от точности. Для строгого формалиста любая математическая теория — всего лишь сочетание знаков, не имеющих значения, как иероглиф, лишенный смысла. Большинство математиков являются платонистами по будням, пока работают с теоремами, пропозициями и выводами, и становятся формалистами по выходным, когда оставляют работу и беседуют с философами. Хотя ясно, что Гильберт был формалистом в рамках области оснований математики, нельзя утверждать, что он оставался им в отношении общей концепции науки. Для немецкого математика она не имеет ничего общего с произвольностью игры. Здесь скорее закрытая подкрепленная внутренней необходимостью концептуальная система, в которой новым идеям всегда соответствуют новые знаки и манипуляции. В итоге формализм оказался самым сильным течением, хотя его стремление к надежной математике, расцениваемой как наука о формальных системах, разбилось о теоремы Гёделя. И ошибка представителей этого течения, как и других, заключается в предположении, что науки базируются на своих собственных основаниях. Во время кризиса оснований не было речи об опасности обрушения многовекового здания математики. Довольно распространенный миф заключается в том, что логико-формальные решения поддержали руины, потому что математика продолжала развиваться и никто не заметил трещин. Но все-таки она переживала золотой век с его блестящими достижениями (теория меры, функциональный анализ, топология...). А неудачно названный кризис оснований, который намечался только в области логики и теории множеств, был скорее кризисом методов, который обновил подход к математике. Гильберт был чемпионом по аксиоматике, сторонником аксиоматического метода не только в математике, но и в науке в целом. Под его покровительством этот метод распространился от корней до кроны математического дерева. Но, оставив в стороне брешь, обнаруженную Гёделем, следует сказать, что аксиоматизм Гильберта не сочетается с рутиной математика — с тем, с чем он сталкивается постоянно. Если мы посмотрим на математика за работой, поскольку статьи — всего лишь продукты его деятельности, то удивимся, сколько неформальных рассуждений он выдает. Что доказывают ограничительные теоремы Гёделя или Тарского для математика в действии? Что математика — слишком крупный кролик для того, чтобы вытащить его из столь маленького цилиндра аксиоматической системы, каким бы ловким ни был этот фокусник Гильберт. Более того, аксиоматика возможна, только если ей предшествовала фаза работы с моделью, то есть аксиомы чисел могут быть сформулированы, если уже есть некоторое представление о том объекте, с которым мы имеем дело. Генетический метод предшествует аксиоматическому, и замена первого вторым предполагает похищение честно заработанного (аксиоматика немедленно присваивает себе все построенное). Могила Гильберта в Гёттингене. У основания памятника высечена знаменитая фраза «Мы должны знать. Мы будем знать».
Могила Гильберта в Гёттингене. У основания памятника высечена знаменитая фраза «Мы должны знать. Мы будем знать».
 Альфред Тарский и Курт Гёдель в Вене в 1935 году. Своими ограничительными теоремами оба поспособствовали разрушению возведенной Г ильбертом конструкции математики.
Альфред Тарский и Курт Гёдель в Вене в 1935 году. Своими ограничительными теоремами оба поспособствовали разрушению возведенной Г ильбертом конструкции математики.
 Давид Гильберт, 1930-е годы.
Давид Гильберт, 1930-е годы.
БУРБАКИ
После Второй мировой войны ультраформалистская концепция математики сформировалась в виде бурбакизма. Группа молодых французских математиков (Андре Вейль, Анри Картан, Жан Дьёдонне и другие) собралась в 1935 году и решила назвать себя именем потерпевшего поражение французского генерала Бурбаки, поскольку еще в университете один шутник-студент, учившийся на курс старше, подбросил им неверные теоремы, носящие имена известных генералов. Коллектив Бурбаки подписывался под многочисленными докладами и монографиями и считал себя настоящим интеллектуальным наследником Гильберта. Под лозунгом «Долой Евклида!» Бурбаки представлял математику в абстрактном и чистом виде, который выкристаллизовался в виде высокоаксиоматичной работы «Элементы математики». Эта традиция представлять математику как подарок небес, лишенный любой земной неточности, в течение 1970-1980-х годов оказывала влияние на преподавание абстрактной теории множеств в средних школах Европы. Собрание Бурбаки, 1938 год. Слева направо: С. Вейль, Ш. Пизо, А. Вейль, Ж. Дьёдонне, К. Шаботи, Ш. Эресманн и Ж. Дельсарт.
Собрание Бурбаки, 1938 год. Слева направо: С. Вейль, Ш. Пизо, А. Вейль, Ж. Дьёдонне, К. Шаботи, Ш. Эресманн и Ж. Дельсарт.
Даже логические аксиомы и аксиомы теории множеств были получены как результат анализа неформальных доказательств. Кроме того, когда обычный математик рассуждает о континууме действительных чисел, он никогда не думает о нестандартных (счетных) моделях континуума (они существуют, если работать аксиоматически в рамках ZFC, и для заядлого формалиста они столь же справедливы, как и стандартная модель). С точки зрения специалиста в области анализа или топологии, для которого континуум — это операционная реальность, существование счетных моделей означает просто бедность формального языка как средства подражания неформальным рассуждениям. Несмотря на яркость метафоры, введенной Гильбертом, математика — это не здание или храм, она больше похожа на город с его проспектами, кварталами, новостройками и опустевшими домами, огороженными под снос.
ГИБЕЛЬ БОГОВ
С приходом Гитлера к власти в 1933 году Людвиг Бибербах (присоединившийся к нацистской партии) встал во главе математики в Германии, продвигая «арийскую, или немецкую», математику (Deutsche Mathematik). Теория относительности была отвергнута как еврейское мошенничество. Та же участь постигла теорию множеств — вероятно, из-за использования в ней еврейского алфавита для обозначения трансфинитных кардинальных чисел (хотя также сыграло роль то, что Бибербах был сторонником Брауэра в Берлине). Еврейским преподавателям было запрещено вести занятия, и одного за другим их сняли с должностей. Математический институт в Гёттингене быстро сдал позиции, и его международный престиж был утрачен, к большому огорчению Гильберта. Герман Вейль — любимый ученик, который сменил его на кафедре, — был вынужден эмигрировать, поскольку его жена была еврейкой по происхождению, и в итоге он присоединился к Альберту Эйнштейну и Курту Гёделю в Институте перспективных исследований в Принстоне. Рихард Курант был отстранен от работы и обосновался в Нью-Йоркском университете. Бернайс вернулся в Швейцарию. Гильберт был обескуражен новой политической ситуацией в Германии. Как-то он спросил у Блюменталя, своего первого аспиранта, какой курс тот читает, и услышал в ответ, что ему больше не разрешено вести занятия. Старик был ужасно возмущен. Когда на банкете его усадили рядом с новым министром образования и тот спросил: «Как в Гёттингене с математикой теперь, когда его очистили от еврейского влияния?», Гильберт парировал: «Математика в Гёттингене? Но ведь ее уже нет!» С началом Второй мировой войны все стало еще более мрачным. Блюменталь эмигрировал в Нидерланды, однако немцы захватили эту страну в 1940-м и его арестовали. Он умер в том же году в печально известном лагере Терезиенштадт, что на территории современной Чехии. Феликс Хаусдорф, который написал первый учебник по теории множеств, покончил жизнь самоубийством, когда узнал, что ему и его семье предстоит депортация в концентрационный лагерь. Другие, например Банах, выжили, но серьезно пострадали физически, работая «кормителями вшей» в возглавляемом немцами бактериологическом институте, где исследовался тиф. Давид Гильберт умер в Гёттингене 14 февраля 1943 года под рев орудий. На похоронах ученого присутствовали менее дюжины человек. Но сегодня живы слова, ставшие его эпитафией: Wir müssen wissen. Wir werden wissen — «Мы должны знать. Мы будем знать».Список рекомендуемой литературы
Almira, J.M. y Sabina dk Lis, J.C., Hilbert. Matemdtico fundamental, Madrid, Nivola, 2007. Bell, E.T., Los grandes matemdticos, Buenos Aires, Losada, 2010. Boyer, C., Historia de la matemdtica, Madrid, Alianza, 1996. Fresan, J., El sueno de la razon. La logica matemdtica у susparadojas, Barcelona, RBA, 2010. Grattan-Guinness, I. (ed.), Delcdlculo a la teoria de conjuntos, Madrid, Alianza, 1984. Gray, J.J., El reto de Hilbert, Barcelona, Critica, 2003. Hilbert, D., Fundamentos de las Matemdticos, Mexico D.F., UNAM, 1993. Kline, M., Matemdticos: la perdida de la certidumbre, Madrid, Siglo XXI, 1998. Mancosu, P. (ed.), From Brouwer to Hilbert. The Debate on the Foundations of Mathematics in the 1920s, Oxford University Press, 1998. Mosteri'n, J., Los logicos, Madrid, Espasa-Calpe, 2000. Odifreddi, P., La matemdtica del siglo xx, Madrid, Katz Barpal Editores, 2006. Reid, C., Hilbert, Nueva York, Springer Verlag, 1970. Stewart, I., Historia de las matemdticos, Barcelona, Critica, 2008. Torretti, R., El paraiso de Cantor, Santiago de Chile, Editorial Universitaria, 1998.Указатель
Entscheidungsproblem, или проблема разрешения 160, 161 ignorabimus 52, 53 Pnncipia mathematica 121-122, 156 Аккерман, Вильгельм 13, 111, 141, 149, 150, 152 аксиома выбора 126, 128, 130, 131, 141, 162 параллельных прямых 28, 29, 31, 32, 36, 38, 42, 44, 162 анализ 8-11, 18, 26, 35, 44, 46, 50, 53, 56, 60, 61, 65, 69, 72, 77, 80, 81, 92-96, 101, 104, 106, 107, 112, 114, 130, 131, 137, 138, 147-149, 155, 164, 167 Банах, Стефан 98, 132, 168 Бернайс, Пауль 13, 111, 113, 128, 141, 150, 153, 158, 162, 168 бесконечность 11, 29, 93-95, 105, 107, 109, 112, 121, 124, 126-128, 134, 136, 137, 147, 151-154, 160, 161 актуальная 152 Бибербах, Людвиг 59, 167 Блюменталь, Отто 65, 67, 168 Бойяи, Янош 31-32, 85 Борн, Макс 99, 102, 103 Брауэр, Лёйтзен Эгберт Ян 11, 109, 131-137, 139-143, 148, 167 Бурбаки 166 вариационное исчисление 13, 60, 61, 63, 79, 72, 79-83, 88, 90, 94 Варинга гипотеза 85 Вейерштрасс, Карл 17, 67, 79, 83, 114 Вейль, Герман 64, 67, 102, 123, 138, 139-140, 142, 143, 167 Гаусс, Карл Фридрих 7, 8, 12, 18, 23, 24, 31, 32, 35, 39, 43, 65, 71, 78, 87, 134, 136 Гейзенберг, Вернер 99, 100, 102, 103, 104, 108 Гейтинг, Аренд 136, 138, 154 геометрия евклидова 18, 28, 30-36, 40, 42-45, 89, 95, 112 неевклидова 15, 18, 26, 28-34, 38, 40, 42-44, 46, 87 Герц, Генрих Рудольф 41, 56, 71 Гёдель, Курт 9, 11, 13, 42, 53, 62, 112, 113, 138, 145, 150, 154- 162, 164, 165, 167 теорема о полноте 37, 150, 158, 160 теоремы о неполноте 11, 42, 154, 156, 158, 159 Гёттингенский университет 9, 13, 19, 24, 35, 39, 49, 55, 65, 67, 71, 72, 84, 88, 90, 93, 99, 100, 103, 111, 121, 127, 142, 153, 167, 168 Гильберта бесконечный отель 121 кривая 133 проблемы 53, 57, 62, 64, 65, 82, 100, 162 программа 140, 145, 147, 150, 153, 154, 162 гильбертово пространство 10, 69, 93-97, 106-108 Гордан, Пауль 19-22, 45, 142 Гордана проблема 13, 15, 19, 22 Дедекинд, Рихард 37, 114, 117, 124, 126, 138, 143 Ден, Макс 54, 62, 67 Дирак, Поль 103-107 Дирихле, Петер Густав Лежён 77 проблема 13, 77-79, 82, 83, 93 доведение до абсурда 20, 21, 136, 137 доказательство 8, 20-22, 24-26, 28, 41, 52, 57, 61, 102, 114, 125, 128, 134, 141, 142, 149-152, 154, 156-159, 161, 167 конструктивное 12, 20, 22, 112, 135, 136, 138, 142 экзистенциальное 12, 20, 22, 112, 136, 141, 142 Евклид 7, 21, 25-28, 31, 32, 35-37, 44, 142, 166 инварианты 13, 19, 20, 22-24, 35, 49, 85 интуиционизм 11, 132-143, 147, 154, 163 истина 8, 27, 38, 41-44, 52, 53, 112, 116, 120, 122, 123, 134, 135, 136, 142, 145, 150, 151, 154, 155-159, 162-163 Кант, Иммануил 7, 17, 35, 43, 132, 134, 137, 139 Кантор, Георг 11, 24, 43, 53, 112— 114, 124-127, 129, 130, 133, 136, 137, 141, 143, 161, 162 категориальность 161 квантовая механика 10, 13, 62, 65, 69, 72, 83, 92-94, 98-100, 103-108 класс 113, 116-119, 122, 123, 127-129 Клейн, Феликс 13, 19, 21, 22, 24, 30, 40, 50, 55, 60, 67, 71, 84, 91, 131 континуум-гипотеза 10, 53, 60, 62, 126, 130, 149, 161, 162 Коэн, Пол 62, 161, 162 Кронекер, Леопольд 17, 20, 58, 63, 67, 127, 132, 136, 137, 139, 142, 143, 147 Лобачевский, Николай 31, 32 логицизм 11, 109, 115, 118, 121, 134, 141, 153, 163 Международный конгресс математиков 1897 г., Цюрих 50 1900 г., Париж 9, 13, 47, 49, 51, 60, 71, 72, 140, 147, 156 1904 г., Гейдельберг 147 1928 г., Болонья 91, 160 Минковский, Герман 9, 13, 18, 24, 50, 55, 71, 85-87, 89, 96, 97, 139 множество кардинальное число 124, 127 несчетное 124, 125, 129, 137, 160 счетное 124-126, 129, 137, 138, 158, 160, 161, 167 независимость 38, 40, 42, 162 Нейман, Джон фон 9, 62, 72, 95, 97, 106-108, 128-129, 152, 154, 155 непротиворечивость 11, 13, 37, 40-42, 54, 61, 62, 141, 147-154, 156, 158, 160, 162 Нордгейм, Лотар Вольфганг 72, 106 оснований кризис 109, 111, 140, 147, 153, 164 «Основания геометрии» 9, 15, 35, 39, 42-46, 71, 148 «Отчет о числах» 26, 35 парадокс 109, 118-124, 127, 128, 129-132, 136, 137, 141, 149, 159 Банаха — Тарского 132 Кантора 127, 128, 129 лжеца 120, 156, 159 Рассела 118, 119, 121, 122, 127-129 Скулема 160 Паш, Мориц 34-36, 41 Пеано, Джузеппе 34, 35, 41, 65, 117, 120, 133, 138, 152, 156, 160 аксиомы 117, 152, 160 платонизм 112, 113, 135, 141, 163 полнота 36. 37, 42, 150, 152-154, 157, 158, 160 принцип индукции 117, 120, 123, 134, 148, 152, 153 исключенного третьего 136, 142 Пуанкаре, Анри 8, 9, 11, 19, 26, 40, 45, 50-52, 59-61, 63-65, 84-86, 97, 119, 120, 132-135, 139, 148, 152 Рассел, Бертран 11, 109, 118-123, 127-131, 134, 148 Риман, Бернхард 24, 32, 34, 40, 64, 71, 78, 87, 92, 93, 96, 124, 134 Римана гипотеза 10, 57, 61, 62, 64, 94 Робинсон, Джулия 58, 159 Тарский, Альфред 42, 159, 164, 165 теорема о невыразимости 159 теория множеств 10, 54, 62, 104, 109, 112, 123, 124, 126-128, 136, 137, 141, 149, 150, 153, 155, 161, 162, 164, 167, 168 относительности 13, 69, 71, 72, 83, 84, 86-91, 97, 167 типов 122 чисел 13, 15, 18, 19, 24, 34, 35, 49, 53, 57, 58, 61, 85 Тьюринг, Алан 160, 161 Уайтхед, Альфред Норт 120-123, 148 уравнение в частных производных 72-77, 82, 100 дифференциальное 18, 59, 60, 61, 63, 72-75, 77, 81, 93, 102, 103 интегральное 13, 69, 72, 73, 92-96, 103, 105-107 потенциала, или Лапласа 75- 77, 82, 93 формализм 11, 13, 36, 86, 94, 107, 108, 132, 134, 138, 141, 147, 154, 156, 162, 163 Фреге, Готлоб 11, 43-46, 109, 115— 120, 123, 134, 143, 149 Хаусдорф, Феликс 130, 168 Цермело, Эрнст 67, 127, 128, 130— 132, 134, 149, 156, 159 Чёрч, Алонзо 160 Шмидт, Эрхард 67, 96, 106 Шрёдингер, Эрвин 100, 102-104, 106, 108 Эйнштейн, Альберт 7, 9, 10, 13, 69, 84, 86-92, 97, 99, 143, 167
Давид Гильберт намеревался привести математику из методологического хаоса, в который она погрузилась в конце XIX века, к порядку посредством аксиомы, обосновавшей ее непротиворечиво и полно. В итоге этот эпохальный проект провалился, но сама попытка навсегда изменила облик всей дисциплины. Чтобы избавить математику от противоречий, сделать ее «идеальной», Гильберт исследовал ее вдоль и поперек, даже углубился в физику, чтобы предоставить квантовой механике структуру, названную позже его именем, - гильбертово пространство. Среди коллег этого незаурядного ученого выделяла невероятная харизма, а знаменитые 23 кардинальные проблемы, сформулированные им в 1900 году, предопределили развитие самой дисциплины на десятилетия вперед. Он превратил город Гёттинген в мировую столицу математики, но стал свидетелем того, как его разоряют нацистские зачистки. Знаменитая фраза «Мы должны знать. Мы будем знать», выгравированная на его могиле, передает жажду знаний последнего великого математика-универсала.
Последние комментарии
3 дней 15 часов назад
4 дней 3 часов назад
4 дней 4 часов назад
4 дней 15 часов назад
5 дней 9 часов назад
5 дней 22 часов назад