Моделирование канала коротковолновой радиосвязи [Владимир Иванович Шлома] (fb2) читать онлайн
- Моделирование канала коротковолновой радиосвязи 1 Мб, 28с. скачать: (fb2) читать: (полностью) - (постранично) - Владимир Иванович Шлома
[Настройки текста] [Cбросить фильтры]
[Оглавление]
Владимир Шлома Моделирование канала коротковолновой радиосвязи
Информация о научной работе
Реферат: В работе предложена методика расчета отношения сигнал/шум для заданных трассы КВ радиосвязи, времени года и времени суток, с использованием оперативного прогноза станций ИЗМИРАН для определения напряженности поля сигнала в заданной точке приема. Поскольку напряженность электрического поля помехи в точке приема в соответствии с МСЭ-R P.372-9 определяется для условной антенны симметричный вибратор, находящейся в свободном пространстве, а на практике имеем дело в основном со штатными для приемных центров антеннами ВГД, выведены формулы для пересчета мощности помехи, рассчитываемой в соответствии с МСЭ-R P.372-9 для условной антенны, в мощность помехи, принимаемой реальной антенной ВГД. Рассмотрены различные способы моделирования помехи с огибающими, распределенными по нормальному, логнормальному и полунормальному законам распределения, проанализирована возможность и адекватность их применения, даны рекомендации по их применению. Разработана программа KVkanal для Matlab, приведенная в приложении А, в которой вычисляется отношение сигнал/шум для каждой из действующих помех и для суммарной помехи, а также мощность помехи, которую требуется создавать при моделировании КВ радиоканала. Инструкция по работе с программой KVkanal приведена в приложении Б. Депонировано №122/В217 от 05.10.2017 г. в Федеральном государственном бюджетном учреждении науки Всероссийский институт научной и технической информации Российской академии наук (ВИНИТИ РАН), г. Москва.Ключевые слова: радиосвязь, коротковолновая радиосвязь, канал связи, напряженность поля, диаграмма направленности, симметричный вибратор, закон распределения, мощность помех, мощность сигнала. Abstract: In work the design procedure of the relation a signal/noise for set lines КВ of a radio communication, a season and time of days, with use of the operative forecast of stations IZMIRAN for definition of intensity of a field of a signal in the set point of reception is offered. As intensity of electric field of a hindrance in a reception point, according to
МСЭ-R P.372-9, is defined for the conditional aerial the symmetric vibrator which are in free space, and in practice we deal basically with regular aerials VGD for the reception centres, formulas for recalculation of capacity of the hindrance counted according to МСЭ-R P.372-9 for the conditional aerial, in capacity of the hindrance accepted by real aerial VGD are deduced. Various ways of modelling of a hindrance with bending around, distributed on normal are considered, логнормальному and to seminormal laws of distribution, possibility and adequacy of their application is analysed, recommendations about their application are given. Program KVkanal for Matlab, resulted in appendix A in which the relation a signal/noise for each of operating hindrances and for a total hindrance is calculated, and also capacity of a hindrance which is required to be created at modelling КВ of a radio channel is developed. The instruction on work with program KVkanal is resulted in the appendix Б. Key Words: radio communication, short-wave radio communication, communication channel, intensity of a field, the orientation diagramme, the symmetric vibrator, the distribution law, capacity of hindrances, capacity of a signal.
Введение
Для прогнозирования качества работы канала КВ радиосвязи или для оценки качества работы вновь разработанных средств радиосвязи без проведения натурных испытаний требуется моделировать такой канал радиосвязи с помощью ПЭВМ. В настоящее время такое моделирование можно осуществлять с использованием данных сети ионосферных станций ИЗМИРАН. Пример оперативного прогноза станций ИЗМИРАН приведен на рис. 1.
Рисунок 1. Пример оперативного прогноза.
Для прогнозирования качества КВ радиосвязи нужно оценить прогнозируемое отношение с/ш на входе приемника, для чего нужно знать напряженности электрического поля сигнала и помехи в точке приема. Напряженность электрического поля сигнала определяется по таблицам 1 и 2 из рисунка 1 для выбранной рабочей частоты, которая должна выбираться как можно ближе к максимально применимой частоте (МПЧ) для обеспечения минимального затухания сигнала. При применении направленных антенн понадобиться также угол прихода сигнала для определения коэффициента усиления антенны. Будем считать, что в точке приема используется направленная на корреспондента стандартная для приемных центров России антенна Надененко ВГДШ c длиной плеча
 и с высотой подвеса h=λ/2.
Напряженность электрического поля шума в точке приема определяется в соответствии с рекомендациями МСЭ-R P.372-9 [3]. Основными видами шума в КВ диапазоне являются промышленные помехи, атмосферные помехи за счет удаленных грозовых разрядов и галактический шум. Тепловые шумы в этом диапазоне вносят незначительный вклад и их можно не учитывать.
По предлагаемой ниже методике рассчитывается отношение сигнал/шум на входе приемника в заданной точке приема для заданного времени года и времени суток. На основе полученного отношения сигнал/шум производится моделирование канала КВ радиосвязи для заданной трассы и заданного времени работы.
и с высотой подвеса h=λ/2.
Напряженность электрического поля шума в точке приема определяется в соответствии с рекомендациями МСЭ-R P.372-9 [3]. Основными видами шума в КВ диапазоне являются промышленные помехи, атмосферные помехи за счет удаленных грозовых разрядов и галактический шум. Тепловые шумы в этом диапазоне вносят незначительный вклад и их можно не учитывать.
По предлагаемой ниже методике рассчитывается отношение сигнал/шум на входе приемника в заданной точке приема для заданного времени года и времени суток. На основе полученного отношения сигнал/шум производится моделирование канала КВ радиосвязи для заданной трассы и заданного времени работы.
Расчет отношения сигнал/шум на входе приемника

Отношение с/ш обычно обозначается , и вычисляется по формуле:

где Рс – мощность сигнала на входе приемника; Рп – мощность шума (помехи) на входе приемника. Зная напряженность поля сигнала в точке приема Ес и параметры приемной антенны, по формулам, приведенным в [2], можно определить напряжение сигнала Uс на входе приемника:
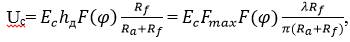
(1) где F(φ) – функция направленности антенны в вертикальной плоскости; Ra – волновое сопротивление антенны; Rf – волновое сопротивление фидера;

– действующая длина антенны, где Fmax – максимальное значение функции направленности. Соответственно мощность сигнала будет определяться по формуле:

Напряжение помехи рассчитывается по формулам, приведенным в [3] для симметричного полуволнового вибратора в свободном пространстве, то есть, без учета влияния земли. Поскольку в качестве приемной антенны у нас используется симметричный вибратор с характеристиками от полуволнового до волнового и высотой подвеса h=λ/2, диаграмма направленности которого отличается от диаграммы направленности полуволнового вибратора в свободном пространстве, нужно определить коэффициент для пересчета напряжения шума. Для этого сравним диаграммы направленности полуволнового и волнового симметричных вибраторов. Функция направленности симметричного вибратора, находящегося в свободном пространстве в плоскости, проходящей через ось вибратора записывается в виде [2]:

(2) где k=2π/λ – волновое число; – длина плеча вибратора в частях длины волны λ; α – угол в радианах, отсчитываемый от оси вибратора. Поскольку для полуволнового симметричного вибратора =λ/4, то для него функция направленности запишется:

(3) Максимальное значение F(α)λ/2max=1 при α=π/2. Функцию направленности в плоскости, перпендикулярной оси вибратора можно записать:

(4) Для волнового симметричного вибратора =λ/2 и функция направленности будет иметь вид:

(5) Максимальное значение F(α)λmax=2 при α=π/2. Функцию направленности в плоскости, перпендикулярной оси вибратора можно записать:

(6) Влияние земли на диаграмму направленности антенны учитывают с помощью формулы [2]:

(7) где ko – коэффициент отражения от земли, примем ko=1; h=λ/2 – высота подвеса антенны; β – сдвиг фаз между антенной и ее зеркальным отражением, для горизонтальных антенн β=180о; φ1 – угол, отсчитываемый от вертикали. Тогда

(8) После перехода к дополнительному углу φ=90о-φ1, отсчитываемому от поверхности земли, будем иметь:

(9) Тогда функции направленности полуволнового и волнового вибраторов в вертикальной плоскости можно записать:

(10) (11) Максимальные значения этих функций будут F(φ)λ/2max=2 и F(φ)λmax=4, при двух значениях углов φ=30о и φ=150о.


Максимальные значения функций направленности в плоскости вибратора и в плоскости перпендикулярной оси вибратора должны быть равны. Если максимальное значение функции направленности в плоскости перпендикулярной оси вибратора увеличилось в раз, то и в плоскости проходящей через ось вибратора и расположенной под углом к горизонту, соответствующему максимальному значению функции направленности в плоскости перпендикулярной оси вибратора, максимальное значение увеличилось в раз. Поэтому, функции направленности в плоскости проходящей через ось вибратора и расположенной под углом φ =30 о к горизонту, то есть плоскости, проходящей через середину одного из двух лепестков диаграммы направленности, нужно пересчитать по формулам:
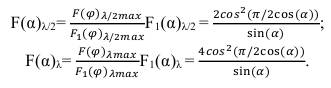
(12) (13) В дальнейшем приведенные выше функции направленности (12) и (13) будем считать функциями диаграммы направленности в горизонтальной плоскости. Мощность помехи, приходящей с некоторого направления под углами α и φ будет определяться по формуле:

(14) где Uп – напряжение помехи на входе приемника;

– действующая длина антенны;
Ra – волновое сопротивление антенны; Rf – волновое сопротивление фидера; Eп – напряженность поля помехи в точке приема;

– коэффициент пропорциональности;

– функция направленности антенны;

– нормированная функция направленности антенны; Fmax – максимальное значение функции направленности антенны. Будем считать, что помеха принимается антенной со всех направлений верхней полусферы с одинаковой интенсивностью, фазы случайны и равновероятны. Тогда мощность принимаемых помех будет суммой элементарных мощностей ΔРп, то есть интегралом по полусфере:

(15) где

(16) где

– нормированная функция направленности в горизонтальной плоскости;

– нормированная функция направленности в вертикальной плоскости. Мощность помех, принимаемых из верхней полусферы эквивалентной антенной (симметричным полуволновым вибратором в свободном пространстве), для которого Fн(φ)=1 и Fmax=1, будет вычисляться по формуле:

(17) Чтобы перейти от мощности помех в эквивалентной антенне к мощности помех в реальной антенне, введем коэффициент пересчета, определяемый как:

(18) Тогда мощность помехи в реальной антенне будет вычисляться по формуле:

(19) Подставив в формулу (18) значения Рп и Рпэ из (15) и (17), получим выражение для вычисления коэффициента пересчета:

(20) Вычислим значения коэффициентов пересчета для двух реальных антенн с высотой подвеса над землей h=λ/2, полуволнового симметричного вибратора и волнового симметричного вибратора.


Расчет напряжения промышленных и галактических помех и отношения сигнал/шум на входе приемника
Медианные значения коэффициентов промышленного и галактического шума приведены на рис. 10 в рекомендациях МСЭ-R P.372-9 [3]. Для получения этих значений также можно воспользоваться следующей формулой [3]: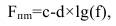
(21) где f – рабочая частота в МГц; c и d – коэффициенты, приведенные в таблице 1. Таблица 1. Значения параметров

В таблице для примера приведены коэффициенты только для тех категорий окружающей среды, в которых размещаются приемные центры. В таблице также приведены децили коэффициента шума относительно медианного значения и соответствующие среднеквадратические отклонения, рассчитанные по формуле (22) для верхней децили. Верхняя дециль Du соответствует случайной величине, не превышаемой в течение 90% времени. Нижняя дециль Dl соответствует случайной величине, не превышаемой в течение 10% времени. Среднеквадратическое отклонение σ соответствует случайной величине, не превышаемой в течение 84% времени.
Медианные значения коэффициентов промышленного и галактического шума Fппm и Fпgm рассчитываем по формуле (21), причем для галактического шума только для частот f≥10МГц. Среднеквадратическое отклонение коэффициента промышленного шума от медианного значения σ определяется по графику интегральной функции распределения или по формуле:

(22) или можно взять из таблицы 1 уже рассчитанное, а для галактической помехи, в соответствии с таблицей 1, σ=1,56 (дБ). Медианное значение напряженности электрического поля помехи в точке приема для эквивалентной антенны, которой является симметричный горизонтальный диполь длиной λ/2, находящийся в свободном пространстве, то есть, без учета влияния земли, будет определяться по формуле:

(23) где f – рабочая частота в МГц; b – полоса пропускания приемника в Гц. Переходя от (дБ) к (мкВ/м) получаем:

(24) Подставляя в формулу (23) вместо Fa(дБ) значения Fппm и Fпgm, а затем переводя в (мкВ/м) по формуле (24) вычисляем медианные значения напряженности электрического поля промышленных и галактических помех Eппm и Eпgm в точке приема для эквивалентной антенны. Аналогично по формуле (23) определяем среднеквадратическое отклонение напряженности поля промышленных помех σЕп и галактического шума σЕg в (дБ/мкВ/м) от медианных значений подставляя вместо Fa(дБ) соответствующие значения σ, а затем переводя в (мкВ/м) по формуле (24). Определяем коэффициенты пропорциональности k для промышленной и галактической помехи как отношение среднеквадратических отклонений от медианных значений к медианным значениям:

(25) Определяем действующее значение напряженности поля промышленной и галактической помех Eпп и Eпg в точке приема по формуле:

(26) Напряжение помех на входе приемника при эквивалентной антенне определяется по формуле [2]:

(27) где Ra=300 Ом – волновое сопротивление применяемой антенны; Rf=200 Ом – волновое сопротивление применяемого фидера; Ea=Eп×hd – э.д.с, наводимая в эквивалентной антенне, где Eп – напряженность поля атмосферной помехи в точке приема (формула 26);

– действующая длина эквивалентной антенны,
где λ –длина волны излучения. Несложно показать, что для реальной антенны напряжение помехи будет определяться по формуле:

(28) (29) где Uпm – медианное значение напряжения помех; σU – среднеквадратическое отклонение напряжения помех от медианного значения. Вычисляем напряжение промышленных помех и галактического шума на входе приемника Uпп и Uпg подставляя в формулы (27) и (28) соответствующие значения. Поскольку между величинами Uп и Eп имеется линейная зависимость (формулы (27) и (28)), то из формулы (25) имеем:

(30) Тогда медианное значение напряжения помехи Uпm можно вычислить по формуле:

(31) Соответственно, среднеквадратическое отклонение напряжения помехи от медианного значения будет определяться:

(32) Подставляя в формулы (31) и (32) соответствующие значения, находим медианные значения Uппm и Uпgm, и среднеквадратические отклонения от медианных значений σUп и σUg амплитуды огибающей промышленных помех и галактического шума. Напряжения огибающих промышленных помех и галактического шума распределены по нормальному закону с медианными значениями Uппm и Uпgm, и среднеквадратическими отклонениями огибающей от медианных значений σUп и σUg. Находим отношение с/ш на входе приемника, подключенного к антенне симметричный полуволновой вибратор:

(33)

где – функция направленности антенны в вертикальной плоскости (10), где φ – угол прихода сигнала, отсчитываемый от поверхности земли (рад). Находим отношение с/ш на входе приемника, подключенного к антенне симметричный волновой вибратор:

(34)

где – функция направленности антенны в вертикальной плоскости (11),
Расчет напряжения атмосферных помех и отношения сигнал/шум на входе приемника
В рекомендациях МСЭ-R P.372-9 [3] на рис. 15а – 38а изображены карты мира, на которых приведены ожидаемые медианные значения коэффициента фоновых атмосферных радиошумов Fam(дБ) выше kT0b, на частоте 1 МГц для каждого времени года при 4-часовых временных блоках, время местное, где:
k – постоянная Больцмана = 1,38×10 –23 Дж/K; T0 – эталонная температура (K), принятая равной 290 K; b – ширина полосы приемной системы на уровне мощности шума (Гц). На рис. 2 приведен пример такой карты [3].
Рисунок 2. Пример карты
Изменение Fam с частотой для каждого блока сезон-время можно видеть на рис. 15b – 38b [3], а изменение других параметров шума в зависимости от частоты – на рис. 15с – 38с [3]. В качестве эталонной антенны для этих атмосферных помех примем горизонтальный симметричный полуволновой
 вибратор, размещенный в свободном пространстве. Пример рисунков b и с приведен на рис. 3.
вибратор, размещенный в свободном пространстве. Пример рисунков b и с приведен на рис. 3.
Рисунок 3. Пример рисунков b и с.
Расчет атмосферного шума следует начинать с определения по рис.1 даты и времени сеанса связи и координат точки приема. Далее в рекомендациях МСЭ‑R P.372-9 [3] находим карту мира и графики «b» и «с», соответствующие требуемому сезону и времени суток в точке приема. По координатам точки приема определяем значение Fam(дБ) на частоте 1 МГц. По графику «b» определяем медианное значение Fam(дБ) для выбранной рабочей частоты, а по графику «с» – значение стандартного отклонения σFam(дБ) для выбранной рабочей частоты. Определяем значение коэффициента шума Fa(дБ) для выбранной рабочей частоты:

(35) Определяем по формуле (23) медианное значение напряженности электрического поля Епаm(дБ/мкВ/м) атмосферной помехи в точке приема для симметричного горизонтального диполя длиной λ/2 и переводим в (мкВ/м) по формуле (24).
По графикам «с» находим медианное отклонение напряжения Vdm(дБ) и его стандартное отклонение σVd(дБ) при b=200 Гц. Находим отклонение напряжения от медианного значения Vd для b=200 Гц
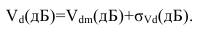
(36) По графику, приведенному в рекомендациях МСЭ-R P.372-9 рис.40 находим отклонение напряжения от среднего значения для заданной полосы пропускания Vdb(дБ). По графику, приведенному в рекомендациях МСЭ-R P.372-9 рис.39 находим превышение напряжения помехи относительно медианного значения для заданной надежности связи А0(дБ). Переходя от (дБ) к (мкВ) имеем:

(37) где Uпаm – медианное значение напряжения атмосферной помехи. Поскольку напряжение помехи пропорционально напряженности поля в точке приема, то по аналогичной формуле можно определять превышение напряженности поля атмосферной помехи в точке приема относительно медианного значения:

(38) где Епam – медианное значение напряженности электрического поля атмосферной помехи в точке приема. Действующее значение напряженности электрического поля атмосферной помехи в точке приема будет определяться по формуле:

(39) Соответственно, коэффициент пропорциональности ka для атмосферной помехи, определяемый по формуле (25), будет равен:

(40) По формуле (27) определяем действующее значение атмосферной помехи на входе приемника при эквивалентной антенне, и по формуле (28) пересчитываем для реальной антенны. Воспользовавшись формулой (33) можно найти медианное значение напряжения атмосферной помехи:

(41) и среднеквадратическое отклонение амплитуды огибающей от медианного значения:
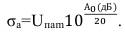
(42) Амплитуда огибающей атмосферной помехи на входе приемника имеет логнормальное распределение. По формулам (33) и (34) находим отношение с/ш на входе приемника, подключенного к антеннам полуволновой и волновой симметричный вибратор.
Расчет напряженности поля и отношения сигнал/шум для суммарной помехи
Отношение с/ш на входе приемника при воздействии суммарной помехи приближенно можно найти по формуле аналогичной (33) или (34):
(43) По формулам, приведенным в [3], можно определить воздействие суммарной помехи путем расчета коэффициента суммарной помехи и его стандартного отклонения. Для этого вычисляем переходные коэффициенты αт и βт по формулам [3]:

(44)
(45) где σi=Dui/1,282 – стандартное отклонение коэффициента шума i-й помехи, рассчитываемое через значение верхней децили; Fami – медианное значение коэффициента шума i-й помехи; с=4,343 – коэффициент. Вычисляем стандартное отклонение коэффициента шума суммарной помехи [3]

(46) Вычисляем медианное значение коэффициента шума суммарной помехи по формуле [3]:
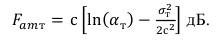
(47) Вычисляем действующее значение коэффициента шума суммарной помехи

(48) Медианное значение напряженности электрического поля суммарной помехи Etm в точке приема для эквивалентной антенны определяется по формуле (23) при подстановке в формулу Famт, затем по формуле (24) переводим в (мкВ/м). Аналогично по формулам (23) и (24) определяем среднеквадратическое отклонение напряженности поля суммарной помехи σЕt. По формуле (25) определяем коэффициенты пропорциональности k для суммарной помехи. Определяем действующее значение напряженности поля суммарной помехи Eпt в точке приема по формуле (26). Напряжение суммарной помехи на входе приемника при эквивалентной антенне определяется по формуле (27). Для реальной антенны напряжение суммарной помехи будет определяться по формуле (28). Медианное значение напряжения суммарной помехи и стандартное отклонение от медианного значения определяем по формулам (31) и (32). По формуле (33) и (34) находим отношение с/ш на входе приемника, подключенного к антеннам полуволновой и волновой симметричный вибраторы. Напряжение суммарной помехи имеет огибающую, распределенную по полунормальному закону. Примечания: Полунормальное распределение – нормальное распределение с удвоенной плотностью вероятности, определенное на половине интервала.
Моделирование канала КВ радиосвязи
Особенности моделирования Для моделирования канала КВ радиосвязи необходимо сформировать высокочастотный сигнал и помеху, действующие на вход радиоприемника. Уровень высокочастотного сигнала может быть фиксированным и превышающим чувствительность приемника, уровень помехи при этом должен регулироваться и соответствовать расчетному отношению с/ш на входе приемника. Как было показано выше, в КВ диапазоне нужно учитывать три основных типа помех: промышленные помехи с нормальным законом распределения, галактический шум с нормальным законом распределения, и атмосферные помехи с логнормальным законом распределения. Для экономии материальных ресурсов есть смысл вместо трех помех формировать две, одну распределенную по нормальному закону, со среднеквадратическим отклонением, определяемым по формуле:
(49) где σх1 и σх2 – среднеквадратические отклонения формируемых промышленной помехи и галактического шума, и вторую – атмосферную помеху с логнормальным распределением. Имеются стандартные программы для формирования случайных величин с такими законами распределения. Еще менее затратным является формирование одной суммарной помехи, распределенной по полунормальному закону. При формировании помех возникают определенные сложности. По методике международного союза электросвязи [3], были определены параметры огибающей этих помех: медианное значение амплитуды огибающей mE и среднеквадратическое отклонение амплитуды огибающей от медианного значения σE. А для формирования помехи нужно знать математическое ожидание случайной величины и среднеквадратическое отклонение формируемой случайной величины х(t) от математического ожидания, обозначим его σх. Кроме того известно, что математическое ожидание помехи равно нулю. Для формирования случайного процесса, соответствующего параметрам огибающей рассчитанной помехи, требуется найти связь между вычисленными выше параметрами огибающей помехи (медианным значением амплитуды огибающей mE и среднеквадратическим отклонение амплитуды огибающей от медианного значения σE), и параметрами формируемой случайной величины. Следует рассмотреть формирование случайных величин с огибающими, распределенными по нормальному и логарифмически нормальному законам распределения. Формирование случайной величины с огибающей, распределенной по нормальному закону. Первый способ. Рассмотрим формирование помехи с огибающей, распределенной по нормальному закону, путем формирования одной случайной величины, распределенной по нормальному закону. Функция распределения случайной величины, распределенной по нормальному закону, записывается в виде:

(50) Определим параметры огибающей этой случайной величины. По аналогии с огибающей сигнала, под огибающей случайного процесса одной случайной величины будем понимать совокупность положительных значений случайного процесса, то есть значения х≥0. Тогда медианное значение огибающей будет определяться как математическое ожидание положительных значений случайного процесса по формуле:

(51) Произведем замену переменной:

(52) Тогда

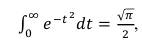
Учитывая, что получим

(53) Дисперсию огибающей, определяем, как второй момент от положительных значений случайного процесса по формуле:
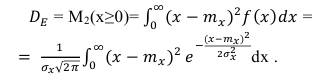
(54) Произведя замену переменной, аналогичную (52), получим:

Произведя интегрирование по частям получим:

(55) (56)
Если помеха, распределенная по нормальному закону, имеет математическое ожидание mx=0 и некоторое среднеквадратическое отклонение от математического ожидания σх, то медианное значение огибающей этого процесса, mE и среднеквадратическое отклонение от медианного значения σE, в соответствии с (44) и (47), всегда будут равны:

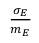

Для такого случайного процесса отношение всегда равно .
Поэтому, таким способом невозможно сформировать помеху с требуемыми параметрами огибающей.
Второй способ. Рассмотрим формирование помехи посредством формирования двух случайных процессов, основного и сопряженного. Итак, требуется сформировать некоторую случайную величину х(t), распределенную по нормальному закону с параметрами: математическое ожидание mx=0, среднеквадратическое отклонение σх, которое зависит от среднеквадратического отклонения огибающей. Определим параметры огибающей этой случайной величины посредством сопряженного процесса [1]. С помощью преобразования Гильберта можно найти некоторую случайную величину y(t), сопряженную с величиной x(t) [1]

(57) Тогда случайную величину x(t) и ей сопряженную y(t) можно представить в виде [1]:

(58) (59) где
 – огибающая случайного процесса, (60)
– огибающая случайного процесса, (60)

– фаза случайного процесса.
(61)
Математическое ожидание случайной величины y(t) my=0, а среднеквадратическое отклонение σy=σх. Определим среднеквадратическое отклонение огибающей σЕ(t) случайного процесса и установим его связь со среднеквадратическим отклонением σх исходного случайного процесса. В формуле (60) под знаком корня квадратного имеются две случайные величины, которые являются квадратичными функциями случайного процесса. Функция плотности вероятности для нормального закона имеет вид [4]:

(62)

Функция плотности вероятности для нормального закона при квадратичной функции случайного процесса приведена в [1] и для u ( t )= x 2 ( t ) и, соответственно, будет иметь вид:

(63) при a=0 функция будет иметь вид:
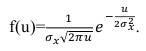
(64) Математическое ожидание этой квадратичной функции mu вычислим как первый момент случайной величины:
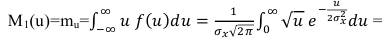
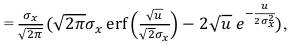
(65) и после подстановки пределов получаем:

(66) Тогда математическое ожидание огибающей случайного процесса, то есть функции E(t), будет определяться:
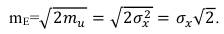
(67) В данном случае математическое ожидание огибающей будет и ее медианным значением. Дисперсию квадратичной функции Du вычислим как второй момент случайной величины:

(68) и после подстановки пределов получаем:

(69) Тогда среднеквадратическое отклонение квадратичной функции будет равно:

(70) Дисперсия огибающей случайного процесса, то есть функции E(t), будет определяться:

(71) Среднеквадратическое отклонение огибающей случайного процесса от медианного значения будет вычисляться по формуле:

(72) Обратим внимание на то, что для случайной величины, распределенной по нормальному закону с математическим ожиданием mx=0, параметры огибающей вычисляются по одной и той же формуле:

Это означает, что в шуме, моделируемом посредством основного и сопряженного процесса, формула (57), соотношение
 всегда будет равно единице. Поэтому этим способом также невозможно смоделировать случайный процесс с требуемыми параметрами огибающей.
всегда будет равно единице. Поэтому этим способом также невозможно смоделировать случайный процесс с требуемыми параметрами огибающей.
Третий способ. Рассмотрим еще один способ формирования помехи посредством формирования двух процессов: процесса, соответствующего среднеквадратическому отклонению от медианного значения огибающей, и процесса, соответствующего медианному значению огибающей. Для этого сформируем случайные величины x(t) огибающей случайного процесса X(t), распределенные по нормальному закону с параметрами: mx=0 и σx. Сформируем случайные величины y(t) случайного процесса Y(t), распределенного по равномерному закону в котором случайная величина может принимать только два значения: y(t)=± my. Вычислим случайные величины z(t)=x(t)+y(t), генерируемого процесса Z(t). Для формирования случайных величин x(t) в MATLAB можно сгенерировать случайную величину x1=rand, распределенную по равномерному закону в диапазоне [0,1], а затем по интегральной функции нормального закона распределения получить случайные величины x(t). Для формирования случайных величин y(t) в MATLAB можно сгенерировать случайную величину y1=randi([0,1],1), распределенную по равномерному закону и имеющую значения только 0 и 1, а затем сформировать случайную величину y(t) по следующему закону: y= my при y1=1; y= -my при y1=0, или наоборот, это значения не имеет. Рассмотрим формируемую таким способом помеху. Плотность распределения формируемой случайной величины x(t), распределенной по нормальному закону, запишется в виде [4]:

(73) Случайная величина y(t) распределена по равномерному закону и имеет всего два значения +my и –my, вероятность появления которых Р=1/2. Суммарная случайная величина z(t)=x(t)+y(t)=x(t)±my, определена на двух интервалах: z≥0 и z≤0. При z≥0 случайная величина распределена по нормальному закону с параметрами σx и плюс my, а при z≤0 с параметрами σx и минус my. С учетом вероятности появления положительных и отрицательных значений случайной величины ее плотность распределения можно записать в виде:

(74)
(75)
Определим медианное значение огибающей этого случайного процесса в соответствии с (51).

Подставив медианное значение, вычисленное в (53) для нормального закона распределения получим:
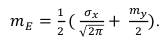
(76) Определим дисперсию огибающей этого случайного процесса в соответствии с (54).

Подставив значение дисперсии огибающей, вычисленное в (55) для нормального закона распределения получим:

Соответственно

(77) Из (76) и (77) найдем значения параметров σx и my, необходимых для формирования случайного процесса с огибающей, соответствующей рассчитанной.
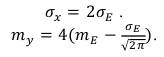
(78) (79) Задача решена. С помощью данного способа имеется возможность формировать случайный процесс с параметрами огибающей, соответствующими требуемым. Формирование случайной величины с огибающей, распределенной по логарифмически нормальному закону. Если случайная величина x(t) распределена по логарифмически нормальному закону, то ее плотность вероятности запишется в виде [4]:

(80)
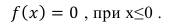
Тогда случайная величина

(81) будет распределена по нормальному закону с плотностью распределения [4]

(82) Как видно из (70) и (71), при переходе от одного закона распределения к другому параметры mx и σx не изменяются, поэтому и параметры случайной величины с огибающей, распределенной по нормальному закону, mE и σE не будут изменяться при переходе к огибающей, распределенной по логарифмически нормальному закону. Из (71) находим формулу для перехода от случайной величины, распределенной по нормальному закону, к случайной величине, распределенной по логарифмически нормальному закону

(83) Способ формирования случайной величины z(t) с огибающей, распределенной по нормальному закону бы определен выше в третьем способе. Остается по формуле, аналогичной (83), от случайной величины z(t) перейти к случайной величине z1(t) с огибающей, распределенной по логарифмически нормальному закону

(84) Таким образом, способ формирования случайной величины с огибающей, распределенной по логарифмически нормальному закону, также определен. Формирование случайной величины с огибающей, распределенной по полунормальному закону. Под полунормальным законом распределения (Half-normal distribution) понимают нормальный закон распределения, заданный на половине интервала, но для которого площадь под кривой спектральной плотности равна площади под кривой спектральной плоскости нормального закона распределения, заданного на всем интервале от -∞ до +∞. В литературе на русском языке упоминание об этом законе распределения встречается крайне редко, в основном под названием «усеченный слева нормальный закон распределения». Плотность распределения и интегральная функция для полунормального закона распределения записывается в виде [5]:
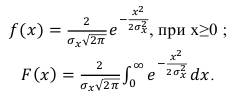
(85)
(86)
Из формулы (85) видно, что это центрированный (mx=0) нормальный закон распределения с удвоенной плотностью, заданный на половине интервала. Определяя по формулам (51) и (54) медианное значение огибающей этого закона распределения и стандартное отклонение от медианного значения получаем:

(87) (88)
Сравнивая с аналогичными параметрами, полученными для нормального закона в (53) и (56), видим, что для полунормального закона распределения эти параметры в два раза больше, чем для нормального закона. Формировать случайную величину с огибающей, распределенной по полунормальному закону будем аналогично рассмотренному выше третьему способу формирования случайной величины, но с учетом значений, полученных в формулах (87) и (88). Медианное значение огибающей и стандартное отклонение от огибающей должны бать в 2 раза больше, чем для огибающей, распределенной по нормальному закону, полученные в (76) и (77), в результате чего будем иметь:

(89) (90) Откуда получаем параметры для формирования случайной величины с огибающей, распределенной по полунормальному закону:

Заключение
Для моделирования радиоканала, сформированные таким образом с помощью ПЭВМ сигнал и помехи следует подать на вход радиоприемного устройства или его имитатора, при этом отношение с/ш на входе радиоприемного устройства для каждого вида помехи должно соответствовать вычисленному значению. Программа расчета параметров для моделирования КВ радиоканала KVkanal приведена в приложении А, инструкция по работе с программой KVkanal приведена в приложении Б.Литература Левин Б.Р. Теоретические основы статистической радиотехники. Издательство «Советское радио», М-1969. Надененко С.И. Антенны Государственное издательство литературы по вопросам связи и радио, М-1959. Рекомендация МСЭ-R Р.372-9 Радиошум, 2007. Вентцель Е.С. Теория вероятностей. Издательство «Наука», М-1969. Википедия (на английском языке), Half-normal distribution.
Приложение А Программа
KVkanal (Расчет параметров для моделирования КВ радиоканала) Исходный код программыclc; clear; close all; % расчет отношения сигнал/шум на входе приемника в КВ диапазоне % ввод исходных данных D=2600; % км – дальность связи f=11.75; % МГц – рабочая частота Ec=1.28; % мкВ/м – напряженность поля сигнала в точке приема a=7.1; % град. – угол прихода сигнала A=2; % применяемая антенна: A=1 – ближе к полуволновому вибратору; A=2 – ближе к волновому вибратору. Tp=300; % град. К – абсолютная температура входных цепей приемника Ta=40; % град. К – эффективная температура антенны df=3000; % Гц – полоса пропускания приемника (тракта ПЧ) dU=1; % мкВ – чувствительность приемника Fama=45; % дБ – медианное значение коэффициента атмосферного шума dFama=6; % дБ – стандартное отклонение Fama A0=3; % дБ – превышение напряжения огибающей над медианным значением M=1; % категория среды в месте приема: 1 – жилой район, 2 – сельская местность. Ra=300; % Ом – волновое сопротивление антенны Rf=200; % Ом – волновое сопротивление фидера % решение задачи k=1.38e-23; % дж/град. – постоянная Больцмана l=300/f; % длина волны излучения a1=a*pi/180; % рад. – угол прихода сигнала if A==1 F=2*sin(pi*sin(a1)); % функция направленности для полуволновой антенны ВГД в вертикальной плоскости Fmax=2; % максимальное значение диаграммы направленности Kp=8; % коэффициент пересчета мощности помехи из эквивалентной антенны в реальную Ap=' (антенна полуволновой вибратор) '; else F=4*sin(pi*sin(a1)); % функция направленности для волновой антенны ВГД в вертикальной плоскости Fmax=4; % максимальное значение диаграммы направленности Kp=80; % коэффициент пересчета мощности помехи из эквивалентной антенны в реальную Ap=' (антенна волновой вибратор) '; end hd=l*Fmax/pi; % действующая высота симметричного вибратора hde=l/pi; % действующая высота эквивалентной антенны % расчет мощности сигнала Ea=Ec*hd*F; % мкВ – эдс сигнала, наводимая в антенне U=Ea*Rf/(Ra+Rf); % мкВ – амплитуда входного сигнала P=U^2/Rf; % мкВт – мощность входного сигнала % тепловой шум Pha=4e6*k*Ta*df; % мкВт – мощность шума антенны Php=4e6*k*Tp*df; % мкВт – мощностьшума входных цепей приемника Ph=Pha+Php; % мкВт – мощность теплового шума на входе приемника % эфирный шум (атмосферные помехи) Faa=Fama+dFama; % дБ – коэффициент атмосферного шума Epd=Faa+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – напряженность поля помехи в точке приема для заданного df Epm=10^(Epd/20); % мкВ/м – медианное изначение напряженности поля помехи в точке приема ka=10^(A0/20); % коэффициент Ep=Epm*(1+ka); % действующее изначение напряженности поля помехи в точке приема Epa=Ep*hde; % мкВ – эдс помехи, наводимая в эквивалентной антенне Upa=Kp^(1/2)*Epa*Rf/(Ra+Rf); % мкВ – амплитуда атмосферной помехи на выходе реальной антенны Upam=Upa/(1+ka); % медианное изначение напряжения атмосферной помехи на выходе реальной антенны siga=Upam*ka; % стандартное отклонение напряжения атмосферной помехи на выходе реальной антенны от медианного значения sigax=2*siga; % стандартное отклонение моделируемого процесса с нормальным распределением moax=4*(Upam-siga/(2*pi)^(1/2)); % мат. ожидание моделируемого процесса Pap=Upa^2/Rf; % мкВт – мощность атмосферной помехи Pp=(Ph+Pap); % мкВт – мощность атмосферной и тепловой помех на входе приемника h02a=P/Pp; % раз отношение с/ш на входе приемника Pad=10*log10(Pp/P); % дБ требуемый уровень помехи относительно сигнала для имитации канала связи L=D/cos(a1); % км – длина пути луча t=L/300; % сек. – время прохождения пути disp([' Входной сигнал', Ap]); disp(['U=', num2str(U),' мкВ (амплитуда входного сигнала)']); disp(['P=', num2str(P),' мкВт (мощность входного сигнала)']); disp(['Ph=', num2str(Ph),' мкВт (мощность тепловой помехи)']); disp(['L=', num2str(L),' км (длина пути, пройденного лучем)']); disp(['t=', num2str(t),' мсек. (время прохождения пути)']); disp(' Атмосферная помеха. Логнормальное распределение.'); disp(['Pap=', num2str(Pap),' мкВт (мощность атмосферной помехи)']); disp(['h02a=', num2str(h02a),' раз (отношение с/ш)']); if U<dU disp([' Амплитуда входного сигнала меньше чувствительности приемника']); else disp(['sigax=', num2str(sigax),' (требуемое стандартное отклонение моделируемого процесса)']); disp(['moax=', num2str(moax),' (требуемое мат. ожидание моделируемого процесса)']); disp(['Pad=', num2str(Pad),' дБ (требуемая мощность атмосферной помехи относительно мощности входного сигнала для имитации канала связи)']); end % галактический шум if f>10 || f==10 Famg=52.25-10.296*log(f); % дБ – медианное значение коэффициента галактического шума dFamg=1.56; Fag=Famg+1.56; % дБ – коэффициент галактического шума Epgd=Fag+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – напряженность поля помехи в точке приема для заданного df Epgm=Famg+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – медианное значение напряженности поля помехи в точке приема для заданного df dEpg=dFamg+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – стандортное отклонение от медианного значения напряженности поля помехи в точке приема для заданного df kg=10^(dEpg/20)/10^(Epgm/20); % коэффициент Epg=10^(Epgd/20); % мкВ/м – напряженность поля помехи в точке приема Epga=Epg*hde; % мкВ – эдс помехи, наводимая в эквивалентной антенне Upg=Kp^(1/2)*Epga*Rf/(Ra+Rf); % мкВ – амплитуда галактической помехи на выходе реальной антенны Ppg=Upg^2/Rf; % мкВт – мощность галактической помехи Upgm=Upg/(1+kg); % медианное изначение напряжения галактической помехи на выходе реальной антенны sigg=Upgm*kg; % стандартное отклонение напряжения галактической помехи на выходе реальной антенны от медианного значения siggx=2*sigg; % стандартное отклонение моделируемого процесса с нормальным распределением mogx=4*(Upgm-sigg/(2*pi)^(1/2)); % мат. ожидание моделируемого процесса h02g=P/Ppg; % раз отношение с/ш на входе приемника Pgd=10*log(1/h02g); % дБ требуемый уровень помехи относительно сигнала для имитации канала связи disp(' Галактический шум. Нормальное распределение.'); disp(['Ppg=', num2str(Ppg),' мкВт (мощность галактической помехи)']); disp(['h02g=', num2str(h02g),' раз (отношение с/ш)']); disp(['siggx=', num2str(siggx),' (требуемое стандартное отклонение моделируемого процесса)']); disp(['mogx=', num2str(mogx),' (требуемое мат. ожидание моделируемого процесса)']); disp(['Pgd=', num2str(Pgd),' дБ (требуемая мощность галактической помехи относительно мощности входного сигнала для имитации канала связи)']); else Ppg=0; Famg=0; dFamg=0; disp(['Ppg=', num2str(Ppg),' ( галактическая помеха отсутствует)']); end % промышленный шум if M==1 Famp=71.52-11.987*log(f); % дБ – медианное значение коэффициента промышленного шума для жилого района dFamp=8.18; % дБ – стандартное отклонение коэффициента промышленного шума для жилого района Fap=Famp+8.18; % дБ – коэффициент промышленного шума для жилого района Mp=' (жилой район) '; elseif M==2 Famp=66.19-11.987*log(f); % дБ – медианное значение коэффициента промышленного шума для сельской местности dFamp=7.27; % дБ – стандартное отклонение коэффициента промышленного шума для сельской местности Fap=Famp+7.27; % дБ – коэффициент промышленного шума для сельской местности Mp=' (сельская местность) '; end Eppd=Fap+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – напряженность поля помехи в точке приема для заданного df Eppm=Famp+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – медианное значение напряженности поля помехи в точке приема для заданного df dEpp=dFamp+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – стандортное отклонение от медианного значения напряженности поля помехи в точке приема для заданного df kp=10^(dEpp/20)/10^(Eppm/20); % коэффициент Epp=10^(Eppd/20); % мкВ/м – напряженность поля помехи в точке приема Eppa=Epp*hde; % мкВ – эдс помехи, наводимая в эквивалентной антенне Upp=Kp^(1/2)*Eppa*Rf/(Ra+Rf); % мкВ – амплитуда промышленной помехи на выходе реальной антенны Ppp=Upp^2/Rf; % мкВт – мощность промышленной помехи Uppm=Upp/(1+kp); % медианное изначение напряжения промышленной помехи на выходе реальной антенны sigp=Uppm*kp; % стандартное отклонение напряжения промышленной помехи на выходе реальной антенны от медианного значения sigpx=2*sigp; % стандартное отклонение моделируемого процесса с нормальным распределением mopx=4*(Uppm-sigp/(2*pi)^(1/2)); % мат. ожидание моделируемого процесса h02p=P/Ppp; % раз отношение с/ш на входе приемника Ppd=10*log10(1/h02p); % дБ требуемый уровень помехи относительно сигнала для имитации канала связи disp([' Промышленная помеха. Нормальное распределение.', Mp]); disp(['Ppp=', num2str(Ppp),' мкВт (мощность промышленной помехи)']); disp(['h02p=', num2str(h02p),' раз (отношение с/ш)']); disp(['sigpx=', num2str(sigpx),' (требуемое стандартное отклонение моделируемого процесса)']); disp(['mopx=', num2str(mopx),' (требуемое мат. ожидание моделируемого процесса)']); disp(['Ppd=', num2str(Ppd),' дБ (требуемая мощность промышленной помехи относительно мощности входного сигнала для имитации канала связи)']); % суммарная помеха h02s=P/(Pp+Ppg+Ppp); % раз отношение с/ш на входе приемника по упрощенной формуле c=4.343; a1=exp(Fama/c+dFama^2/(2*c^2)); % частные промежуточные коэффициенты a2=exp(Famg/c+dFamg^2/(2*c^2)); a3=exp(Famp/c+dFamp^2/(2*c^2)); at=a1+a2+a3; % промежуточный коэффициент bt=a1^2*(exp(dFama^2/(2*c^2))-1)+a2^2*(exp(dFamg^2/(2*c^2))-1)+a3^2*(exp(dFamp^2/(2*c^2))-1); % промежуточный коэффициент sigmt=c*(log(1+bt/at^2))^1/2; % стандартное отклонение коэффициента шума от медианного значения Famt=c*(log(at)-sigmt^2/(2*c^2)); % медианное значение коэффициента шума Fat=Famt+sigmt;% действующее значение коэффициента шума Eptd=Fat+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – действующее значение напряженности поля помехи в точке приема для заданного df Eptm=Famt+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – медианное значение напряженности поля помехи в точке приема для заданного df dEpt=sigmt+20*log10(f)+10*log10(df)-99; % дБ/мкВ/м – стандортное отклонение от медианного значения напряженности поля помехи в точке приема для заданного df kt=10^(dEpt/20)/10^(Eptm/20); % коэффициент Ept=10^(Eptd/20); % мкВ/м – действующее значение напряженности поля помехи в точке приема для заданного df Epta=Ept*hde; % мкВ – эдс суммарной помехи, наводимая в эквивалентной антенне Upt=Kp^(1/2)*Epta*Rf/(Ra+Rf); % мкВ – амплитуда суммарной помехи на выходе реальной антенны Ppt=Upt^2/Rf; % мкВт – мощность суммарной помехи Uptm=Upt/(1+kt); % медианное изначение напряжения суммарной помехи на выходе реальной антенны sigt=Uptm*kt; % стандартное отклонение напряжения суммарной помехи на выходе реальной антенны от медианного значения sigtx=sigt; % стандартное отклонение моделируемого процесса с нормальным распределением motx=2*(Uptm-sigt/(2*pi)^(1/2)); % мат. ожидание моделируемого процесса h02t=P/Ppt; Ptd=10*log10(1/h02t); % дБ требуемый уровень помехи относительно сигнала для имитации канала связи disp(' Суммарная помеха. Полунормальное распределение.'); disp(['h02s=', num2str(h02s),' раз (отношение с/ш по упрощенной формуле)']); disp(['Ppt=', num2str(Ppt),' мкВт (мощность суммарной помехи)']); disp(['h02t=', num2str(h02t),' раз (отношение с/ш по формуле для суммарной помехи)']); disp(['sigtx=', num2str(sigtx),' (требуемое стандартное отклонение моделируемого процесса)']); disp(['motx=', num2str(motx),' (требуемое мат. ожидание моделируемого процесса)']); disp(['Ptd=', num2str(Ptd),' дБ (требуемая мощность суммарной помехи относительно мощности входного сигнала для имитации канала связи)']);
Приложение Б Инструкция по работе с программой
KVkanalПрограмма KVkanal работает в среде MATLAB 2011. Для подготовки исходных данных нужно иметь распечатку оперативного прогноза по данным с сети ионосферных станций ИЗМИРАН и рекомендации МСЭ-R P.372-9 (Радиошум). Подготовка исходных данных заключается в определении по распечатке оперативного прогноза даты и времени проведения сеанса связи, координат размещения радиоприемного устройства, дальности связи, рабочей частоты, напряженности поля сигнала в точке приема, угла прихода сигнала, и определении по рекомендациям МСЭ-R P.372-9 медианного значения коэффициента атмосферного шума, стандартного отклонения коэффициента атмосферного шума, и превышение напряжения помехи над медианным значением. Пример распечатки оперативного прогноза приведен на рис. 1.
Рисунок 1. Пример распечатки оперативного прогноза Координаты приемника широта/долгота Время сеанса связи Дата сеанса связи Частота Напряженность поля Угол прихода сигнала Дальность связи По распечатке оперативного прогноза выбирается оптимальное модовое распространение (обычно по максимальному значению напряженности поля в точке приема) и для него определяется рабочая частота, которая должна выбираться как можно ближе к максимально применимой частоте (МПЧ) для обеспечения минимального затухания сигнала. Остальные параметры определяются исходя из выбранного модового распространения. Далее, исходя из даты и времени сеанса связи в рекомендациях
МСЭ-R P.372-9 [3] на рис. 15а – 38а выбирается нужная карта мира, соответствующая требуемому времени года и временному интервалу, по которой определяется ожидаемое медианное значения коэффициента фоновых атмосферных радиошумов Fam(дБ) выше kT0b, на частоте 1 МГц для заданных координат расположения радиоприемника. Рядом с найденной картой в рекомендациях находятся рисунки с таким же номером, что и карта, но с индексами «b» и «c», соответствующие требуемому времени года и временному интервалу. Используя графики, изображенные на рисунке «b», по найденному на предыдущем шаге значению Fam(дБ) выше kT0b, на частоте
1 МГц, находим значение Fam(дБ) для заданной рабочей частоты, а по графику «с» – значение стандартного отклонения σFam(дБ) для выбранной рабочей частоты. Все определенные выше параметры следует ввести в программу в качестве исходных данных. Остается определить еще один параметр исходных данных А0(дБ), соответствующий превышению напряжения помехи относительно медианного значения для заданной надежности связи. Для этого по графикам «с» находим медианное отклонение напряжения Vdm(дБ) и его стандартное отклонение σVd(дБ) при b=200 Гц. Затем находим отклонение напряжения от медианного значения Vd для b=200 Гц по формуле:
Vd(дБ)=Vdm(дБ)+σVd(дБ).
По графику, приведенному в рекомендациях МСЭ-R P.372-9 рис.40 находим отклонение напряжения от среднего значения Vdb(дБ).для нужного отношения заданной полосы пропускания приемника к полосе пропускания в 200 Гц. По графику, приведенному в рекомендациях МСЭ-R P.372-9 рис.39 находим искомое превышение напряжения помехи относительно медианного значения А0(дБ) для заданного процента времени превышения ординаты, под которым следует понимать допустимый процент времени нарушения связи. Полученное значение А0(дБ) и заданное значение полосы пропускания приемника вводим в программу в качестве исходных данных. Определяемся с типом приемной антенны (полуволновой вибратор или волновой) и категорией среды в месте приема (жилой район или сельская местность), и вводим эти параметры в исходные данные. При необходимости можно в исходных данных подкорректировать чувствительность приемника. Остальные исходные данные можно не изменять. Запускаем программу на исполнение, для чего в окне Editor щелкаем мышкой по зеленому значку с изображением треугольника, и в окне Command Window смотрим результаты вычислений.
Последние комментарии
4 часов 20 минут назад
4 часов 28 минут назад
10 часов 41 минут назад
10 часов 44 минут назад
10 часов 55 минут назад
11 часов 1 минута назад