Методики энергетического расчета канала дальней тропосферной радиосвязи [Владимир Иванович Шлома] (fb2) читать онлайн
[Настройки текста] [Cбросить фильтры]
[Оглавление]
Владимир Шлома, Иван Гвозд Методики энергетического расчета канала дальней тропосферной радиосвязи
РЕФЕРАТ
В данной научной работе приведены две методики, в основу которых положены методики, изложенные в книге Ю.И. Давыденко «Дальняя тропосферная связь», и в рекомендациях МСЭ-R P.617, в которые внесены изменения с целью повышения достоверности и сравнимости результатов расчетов по этим методикам, а также выполнена аппроксимация графиков для автоматизации вычислений на ПЭВМ. По предлагаемым методикам вычисляется отношение сигнал/шум на входе приемника и вероятность битовой ошибки при заданных дальности и надежности связи, и предельная дальность связи при заданных вероятности битовой ошибки и надежности связи. Для расчета трасс дальней тропосферной радиосвязи, расположенных на территории бывшего СССР можно применять обе методики и сравнивать результаты вычислений. Для расчета трасс, расположенных за пределами указанной территории, применима только вторая методика. Научная работа опубликована ЦВИФ МО РФ, Сборник рефератов депонированных рукописей, Серия Б, Выпуск №118, инв. В7851. На основе предлагаемых методик разработана «Программа расчета канала ДТР» для вычисления в Matlab, позволяющая вычислять все параметры, определенные в этих методиках. Программу можно скачать бесплатно (через прокси-сервер) по ссылке: http://www.fwirpx.com/file/2354059. Исходный код программы, желающие могут скачать по ссылке: https://www.litres.ru/vladimir-ivanovich-s/energeticheskiy-raschet-kanala-dalney-troposfernoy-ra/.Введение
Задача расчета радиолиний, использующих типовые станции дальней тропосферной радиосвязи (ДТР), состоит в том, чтобы по известным энергетическим параметрам аппаратуры определить дальность связи, при которой будет обеспечена заданная надежность связи. При этом под надежностью связи понимается процент времени по отношению к определенному периоду работы радиолинии, в течение которого обеспечивается заданное качество связи, т. е. заданное отношение сигнал/шум на выходе телефонного канала радиолинии, или заданная достоверность передачи двоичной информации (заданный процент искаженных или не принятых посылок к переданным). Количественно надежность связи определяется вероятностью того, что в течение определенного времени информация будет приниматься с заданным превышением сигнала над шумами на выходе радиолиний. Надежность и дальность связи являются основными характеристиками, определяющими возможности станций. Они неразрывно связаны друг с другом. Нельзя говорить о дальности действия станции без указания, какая при этом обеспечивается надежность связи. Поскольку, с увеличением дальности связи значительно увеличивается ослабление радиоволн на трассе и падает уровень принимаемого сигнала, то естественно, что надежность связи при этом будет уменьшаться. Требования к дальности и надежности связи являются противоречивыми. Можно получить большие дальности при низкой надежности связи и, наоборот, можно обеспечить очень высокую надежность связи при небольшой дальности. Тропосферные радиолинии характеризуются очень длинными трассами, обычно от 100 км до почти 1000 км. Это дает очень сильное ослабление на трассе, что можно компенсироваться использованием очень большой излучаемой мощности, большими коэффициентами усиления антенн и чувствительными малошумящими приемниками. Дополнительно в некоторых случаях может понадобиться разнесение. Используемые диапазоны частот: УВЧ и нижняя часть диапазона СВЧ. Процесс тропосферного распространения происходит над трассами, продолжающимися за пределами нормального радиогоризонта. Существует только две постоянных при процессе тропосферного распространения на частотах выше 30 МГц: дифракция и тропосферное рассеяние. Характерной особенностью тропосферного распространения является многолучёвость сигнала. Искажения, создаваемые задержками многолучёвости, создают интермодуляционный шум в аналоговых линиях и межсимвольные искажения в цифровых линиях. Первые работы по механизму тропосферного распространения появились примерно в 1950 году. После этого в течение приблизительно 15 лет проводилось большое количество теоретических исследований и происходило много научных обсуждений. Превосходство одной или другой теории никогда не признавалось. Однако был признан главный механизм турбулентного рассеяния и неоднородности слоя рефракции [Friis и др., 1957г.], а также, что соответствующие процессы обоих явлений могут вести себя, в основном в зависимости от климатических характеристик рассматриваемого географического района. Были разработаны математические модели, описывающие потери при тропосферном рассеянии, основанные на таких параметрах, как масштаб турбулентности и размер слоя. Однако из-за трудности в получении этих параметров из метеорологических измерений, эти модели не использовались в практических применениях. Поэтому для практического применения использовались методы расчета, использующие эмпирическую или полуэмпирическую модели для вычисления потерь при передаче. В настоящее время прогнозирование тропосферного рассеяния на трассах основано на этих эмпирических или полуэмпирических методах. Два метода были опубликованы в 1965 году и использовались как справочные материалы для исследований МСЭ-R в течение более 20 лет. Один из них соответствует упрощенной версии метода Национального бюро стандартов Соединенных Штатов (НБС), впервые опубликованному в мае 1965 года и затем пересмотренному два года спустя. Международным комитетом по электросвязи были проведены испытания трех наиболее известных методов прогнозирования потерь (Zhang, 1988 г.; Rice и др., 1967 г. и Boithias и Battesti, 1965 г.) на 25 тропосферных трассах. Испытания показали, что метод Zhang, 1988 г. дает погрешность не более 0,7 дБ, в то время как второй метод дает погрешность порядка 3 дБ, а третий – порядка 4,2 дБ. На основании первого метода были разработаны рекомендации МСЭ-R для расчета тропосферных линий связи: РЕКОМЕНДАЦИЯ МСЭ-R P.617-3 – для распространения за счет тропосферного рассеяния, и РЕКОМЕНДАЦИЯ МСЭ-R P.530-15 – для распространения за счет дифракции. Проведенный анализ показал, что для наших целей можно использовать метод расчета трассы для тропосферного рассеяния. Метод расчета трассы для распространения за счет дифракции оказался для наших целей неприемлемым, так как предназначен для расчета конкретной трассы с известным профилем и не может быть применен для расчета обобщенных трасс при неизвестном профиле трассы. Анализ отечественных источников показал, что для расчета обобщенной тропосферной трассы при распространении за счет тропосферного рассеяния наиболее подходит метод, изложенный в книге Ю.В. Давыденко, Дальняя тропосферная связь 1968 г. Как указывает автор, многочисленные испытания этого метода, проводимые в свое время в различных районах СССР, подтвердили достоверность расчета потерь на тропосферных линиях связи порядка 3 дБ. В настоящее время существует много различных методик энергетического расчета канала ДТР в которых используются разные исходные данные и получаются разные результаты вычислений, зачастую, несравнимые между собой. Не имея результатов испытаний станций ДТР, практически невозможно разобраться какие из этих методик дают достоверные результаты, а какие нет. На наш взгляд, как наиболее достоверные, можно отметить две методики: методика, изложенная в книге Ю.И. Давыденко «Дальняя тропосферная связь» [1], предназначенная для расчета радиолиний, расположенных на территории бывшего СССР, и методика, изложенная в рекомендациях МСЭ-R P.617 [2], не имеющая ограничений по расположению радиолиний, но, ввиду ее глобальности, имеющая меньшую достоверность результатов вычислений. К сожалению, в этих методиках рассчитываются разные показатели и непосредственно их нельзя сравнивать, но, после их приведения к одному виду, они дают достаточно близкий результат для расчетов полного затухания на трассе в центральной части России (погрешность порядка 0,5 дБ). Однако, графоаналитический метод, используемый в этих методиках, не позволяет автоматизировать расчеты с использованием ПЭВМ. В данной статье приведены две доработанные методики. В основу первой методики положена методика, изложенная в книге Ю.И. Давыденко «Дальняя тропосферная связь», в которую внесены некоторые изменения с целью повышения достоверности и сравнимости результатов расчетов со второй методикой, а также выполнена аппроксимация графиков для автоматизации вычислений на ПЭВМ. В основу второй методики положена методика, изложенная в рекомендациях МСЭ-R P.617, в которую внесены небольшие изменения для сравнимости результатов с первой методикой, и выполнена аппроксимация графиков. По предлагаемым методикам вычисляется отношение сигнал/шум на входе приемника и вероятность битовой ошибки при заданных дальности и надежности связи, а также предельная дальность связи при заданных вероятности битовой ошибки и надежности связи. 1. Исходные данные: – дальность связи R (км); – рабочая частота fр (МГц); – мощность передатчика Pпер (Вт); – коэффициент шума приемника Fэ (дБ); – кратность разнесения n; – потери мощности в передающем фидере ηпер (дБ); – потери мощности в приемном фидере ηпр (дБ); – усиление антенны передатчика Gпер (дБ); – усиление антенны приемника Gпр (дБ); – ширина ДН антенн в обеих плоскостях α (град); – высота подъема приемной и передающей антенн h (м); – угол горизонта со стороны передатчика θпер (град); – угол горизонта со стороны приемника θпр (град); – режимы работы радиолинии: а) телефонные каналы с частотным уплотнением: 1) № телефонного канала в линейном спектре nт; 2) эффективная девиация частоты на канал Δf (Гц); 3) средняя частота канала в линейном спектреFk=3100×(nт-1)+3100/2+300 (Гц); б) телеграфные виды работы: 1) тип манипуляции: АТ, ЧТ, ФТ, ОФТ или технология OFDM; 2) количество уровней модуляции или несущих М; 3) скорость передачи двоичных сигналов V (кбит/с); 4) вероятность ошибки при передаче бинарной информации Pош для заданного процента времени и заданного периода; – время года: наихудший зимний месяц; лето; весна или осень; – оцениваемый период надежности связи: сутки; месяц; год; – заданный процент времени безотказной работы Т%; – тип приемника: оптимальный (когерентный); квазиоптимальный (некогерентный).
Примечания: 1. Угол горизонта – угол между лучами, проведенными из центра антенны в направлении излучения, один параллельно поверхности земли, а второй – на вершину препятствия. 2. Высоты подъема передающей и приемной антенн предполагаются одинаковыми. 2. Методика расчета для радиолиний, расположенных на территории бывшего СССР В основу предлагаемой методики положена методика, изложенная в книге Ю.И. Давыденко «Дальняя тропосферная связь» [1]. 2.1 Определяем потери в свободном пространстве при использовании изотропных антенн L0изотр=(4πR/λ)2, (2.1) L0изотр(дБ)=22+201g(R/λ), (2.2) где R – дальность в метрах; λ – длина волны в метрах. Для случая использования направленных антенн с коэффициентами усиления Gпер(дБ) и Gпр(дБ) и потерями в фидерах ηпер(дБ) и ηпр(дБ) потери в свободном пространстве будут определяться по формуле [7]: L0(дБ)= L0изотр(дБ)+ηпер(дБ)+ηпр(дБ)-Gпер(дБ)-Gпр(дБ)= =22+201g(R/λ)+ηпер(дБ)+ηпр(дБ)-Gпер(дБ)-Gпр(дБ). (2.3) 2.2 Вычисляем дополнительные потери Lдоп для наихудшего зимнего месяца. Lдоп = Lмед+Lз+Lp+Lh+La+Lк, (2.4) где Lмед – медианные потери; Lз – потери от замираний; Lp – потери, обусловленные влиянием неровностей рельефа местности; Lh – потери, обусловленные влиянием земной поверхности при малых величинах отношения h/λ; La – потери усиления антенн; Lк – климатические потери. Вычисляем каждую составляющую из формулы (2.4). В методике [1] почти все потери вычисляются как положительная величина, за исключением потерь от быстрых замираний и потерь от медленных замираний, которые определяются как отрицательная величина. При этом общие потери для телефонного канала от быстрых и медленных замираний также определяются как положительная величина. Чтобы избавиться от этой путаницы, в предлагаемой методике во всех выведенных формулах потери будут определяться как положительная величина. 2.2.1 Медианные потери Медианные потери Lмед определяются по рис. 1.

Рис. 1. Зависимость медианных величин потерь от расстояния и длины волны для зимнего месяца (сплошные линии – для зоны тропосферного рассеяния, пунктирные – для дифракционной зоны) Для приведенных графиков (сплошные линии на рис. 1) можно записать уравнения типа Lмед=а+b×R: Lмед=62+0,11×R, для λ=3 см; (2.5) Lмед=61,3+0,09×R, для λ=10 см; (2.6) Lмед=58,3+0,08×R, для λ=30 см. (2.7) При аппроксимации коэффициентов а и b получаем формулы для их вычисления в зависимости от λ:

Формула для вычисления Lмед будет иметь вид:

(2.8) где λ(см) – длина волны; R(км) – дальность связи. В случае необходимости определения Lмед для других длин волн можно приближенно считать, что значения Lмед обратно пропорциональны длине волны. Если потребуется оценить потери для летнего или другого времени года, то следует учесть сезонный ход потерь, который можно в среднем принять равным 12 дБ. Таким образом, для летних месяцев нужно значения, приведенные на рис. 1, уменьшить на 12 дБ, а в осенние и весенние месяцы – на 6 дБ. 2.2.2 Потери от замираний Lз. 2.2.2.1 Потери Lз для цифрового канала. В методике [1] в зависимости от времени существования замирания условно разделяются на быстрые (с квазипериодом 0,1
 10 с) и медленные (с квазипериодом от десятков минут до нескольких часов).
Поэтому общие потери от замираний складываются из потерь от быстрых, и от медленных замираний Lз=Lмз+Lбз,
где Lмз – потери от медленных замираний;
Lбз – потери от быстрых замираний.
При расчете радиолиний в режиме передачи бинарных сигналов быстрые и медленные замирания, как и в методике [1], будем учитывать отдельно.
2.2.2.1.1 Расчет потерь от быстрых замираний Lбз.
При передаче бинарных сигналов по каналам с частотным уплотнением (в случае передачи бинарных сигналов по телефонным каналам радиолинии) и при непосредственной модуляции несущей, можно считать, что коэффициент потери надежности ɤ (часть времени, в течение которого будут наблюдаться отказы от быстрых замираний) будет определяться вероятностью опускания сигнала ниже медианного значения за счет быстрых замираний Р(Lб.з.).
ɤ=1-Т%/100, (2.9)
где Т% – заданный процент времени безотказной работы.
P(Lб.з.) – вероятность превышения уровня, соответствующего Lб.з..
Р(Lб.з.) соответствует той части времени ɤ, в течении которого потери будут превышать медианные
ɤ=Р(Lб.з.), (2.10)
или через интегральную функцию:
ɤ=F(Емин/Емед.). (2.11)
Отсюда
F(Емин/Емед.)=Р(Lб.з.)=ɤ. (2.12)
Быстрые замирания в канале дальней тропосферной связи в основном подчиняются релеевскому закону распределения. Интегральная функция релеевского закона распределения определяется по формуле:
10 с) и медленные (с квазипериодом от десятков минут до нескольких часов).
Поэтому общие потери от замираний складываются из потерь от быстрых, и от медленных замираний Lз=Lмз+Lбз,
где Lмз – потери от медленных замираний;
Lбз – потери от быстрых замираний.
При расчете радиолиний в режиме передачи бинарных сигналов быстрые и медленные замирания, как и в методике [1], будем учитывать отдельно.
2.2.2.1.1 Расчет потерь от быстрых замираний Lбз.
При передаче бинарных сигналов по каналам с частотным уплотнением (в случае передачи бинарных сигналов по телефонным каналам радиолинии) и при непосредственной модуляции несущей, можно считать, что коэффициент потери надежности ɤ (часть времени, в течение которого будут наблюдаться отказы от быстрых замираний) будет определяться вероятностью опускания сигнала ниже медианного значения за счет быстрых замираний Р(Lб.з.).
ɤ=1-Т%/100, (2.9)
где Т% – заданный процент времени безотказной работы.
P(Lб.з.) – вероятность превышения уровня, соответствующего Lб.з..
Р(Lб.з.) соответствует той части времени ɤ, в течении которого потери будут превышать медианные
ɤ=Р(Lб.з.), (2.10)
или через интегральную функцию:
ɤ=F(Емин/Емед.). (2.11)
Отсюда
F(Емин/Емед.)=Р(Lб.з.)=ɤ. (2.12)
Быстрые замирания в канале дальней тропосферной связи в основном подчиняются релеевскому закону распределения. Интегральная функция релеевского закона распределения определяется по формуле:

(2.13) На рис. 2 показаны графики интегральных функций релеевского закона распределения для σ=-1,5 дБ (красная линия), и для σ=18,5 дБ (синие точки). По оси Х отложено отношение Емин/Емед=Lбз в дБ, по оси Y – F(Емин/Емед), вероятность не превышения уровня потерь, отложенного по оси Х, при одинарном приеме.

Рис. 2. Графики интегральных функций релеевского закона распределения
Как видно из графиков, с увеличением σ кривая смещается вправо на соответствующее значение дБ параллельно первоначальному положению без изменения угла наклона. Поэтому глубина быстрых замираний относительно медианного значения Lбз, определяемая как разница между медианным значением при F(Емин/Емед)=0,5 и значением Емин/Емед при F(Емин/Емед)=ɤ, не зависит от σ и зависит только от заданного ɤ. Поэтому при расчетах Lбз удобно пользоваться графиком, построенным для σ=-1,5 дБ, у которого медианный уровень 50% соответствует затуханию 0 дБ. Lбз од=-Емин/Емед(ɤ=F). (2.14) Подставив значение F(x) из (2.13) в (2.14) получим:

(2.15) Тогда для одинарного приема

(2.16) С учетом (2.9) для одинарного приема будем иметь

(2.17) Величину Lбз для сдвоенного и счетверенного приема в [1] и [3] предлагается определять по разным графикам, причем результаты значительно отличаются друг от друга. В [1] определять величину Lбз для сдвоенного и счетверенного приема рекомендуется по графикам (рис. 3 или 4), соответственно.

Рис. 3. Характеристика распределения для быстрых, релеевских замираний при сдвоенном приеме (оптимальное сложение)

Рис. 4. Характеристика распределения для быстрых, релеевских замираний при счетверенном приеме (оптимальное сложение).
За нуль децибел на графиках принято медианное значение сигнала при одинарном приеме. Под процентом времени здесь понимается величина ɤ=2×Рош×100%, где Рош – заданная вероятность битовой ошибки. В [3] приведены подобные графики, показанные на рис. 3а и 4а.

Рис. 3а. Характеристика распределения для быстрых, релеевских замираний при сдвоенном приеме

Рис. 4а. Характеристика распределения для быстрых, релеевских замираний при счетверенном приеме
Под процентом времени превышения уровня здесь понимается процент времени безотказной работы, что вполне логично. В графиках из [1] зависимость глубины замираний от заданной вероятности битовой ошибки логичной не представляется, поскольку реальный процесс замирания не может зависеть от субъективно заданной нами величины Рош. Поэтому величину быстрых замираний будем определять по графикам из [3] рис. 3а и 4а для случая сложения сигналов с равными коэффициентами усиления. Аппроксимировать эти графики с помощью формул не представляется возможным. Возможна только аппроксимация с помощью Smoothing Spline, что и было выполнено. При вычислении в Matlab можно использовать следующие расчетные подпрограммы с полученными при аппроксимации коэффициентами рр2.* и рр4.*: Для сдвоенного приема: pp2.form='pp'; pp2.breaks=[50 70 80 90 95 98 99 99.5000 99.9000 99.9900]; pp2.coefs=[3.84210275826828e-05,0,0.0796329235178138,-3.70000622094116;-8.80037940540999e-05,0.00230526165496097,0.125738156617033,-1.79997952992342;0.000378860333770322,-0.000334852166662026,0.145442251500023,-0.400075592311095;0.00209556468655813,0.0110309578464476,0.252403308297879,1.39972203979325;0.00544230028577507,0.0424644281448196,0.519880238254215,3.19945811326360;1.31340755735463,0.0914451307167953,0.921608914839060,5.28822078904555;-0.630095933072249,4.03166780278070,5.04472184833655,7.61468239195604;-1.03894174768381,3.08652390317233,8.60381770131306,11.0661982751855;-6.81405113315541,1.83979380595174,10.5743447849627,14.9350769083666;]; pp2.pieces=9; pp2.order=4; pp2.dim=1; Lbz=ppval(pp2,Tpr); Для счетверенного приема: pp4.form='pp'; pp4.breaks=[50 70 80 90 95 98 99 99.5000 99.9000 99.9900]; pp4.coefs=[3.66286868444963e-05,0,0.0453526263896390,-6.20001612140725;-0.000113102179577539,0.00219772121066978,0.0893070506030345,-4.99993409885850;0.000326883867208858,-0.00119534417665639,0.0993308209431684,-4.00019365133871;-0.000727365934956800,0.00861117183960936,0.173489097572698,-2.79953599236381;0.0168400327937770,-0.00229931718474264,0.205048370847032,-1.80773195037969;0.604392422407672,0.149260977959251,0.645933353170556,-0.758599807069293;-0.397553159541230,1.96243824518227,2.75763257631207,0.640986946468185;-0.762714404274230,1.36610850587042,4.42190595183842,2.46071865097713;-1.66981933607921,0.450851220741332,5.14868984248313,4.39924467077825;]; pp4.pieces=9; pp4.order=4; pp4.dim=1; Lbz=ppval(pp4,Tpr); где Lbz – глубина быстрых замираний (дБ); pp2 и pp4 – коэффициенты, полученные при аппроксимации spline; Tpr – процент времени безотказной работы. Примечание: В отличие от графиков рис. 3а и 4а в программе вычисляется глубина замираний, то есть величина уменьшения сигнала ниже медианного уровня, а не превышение над медианным уровнем, как показано на графиках. Поэтому знаки (+ и -) меняются на противоположные. 2.2.2.1.2 Расчет потерь от медленных замираний Lмз. Медленные замирания оцениваются по изменению средних (или медианных) значений уровня сигнала. Экспериментальные характеристики медленных затуханий показаны на рис. 5.
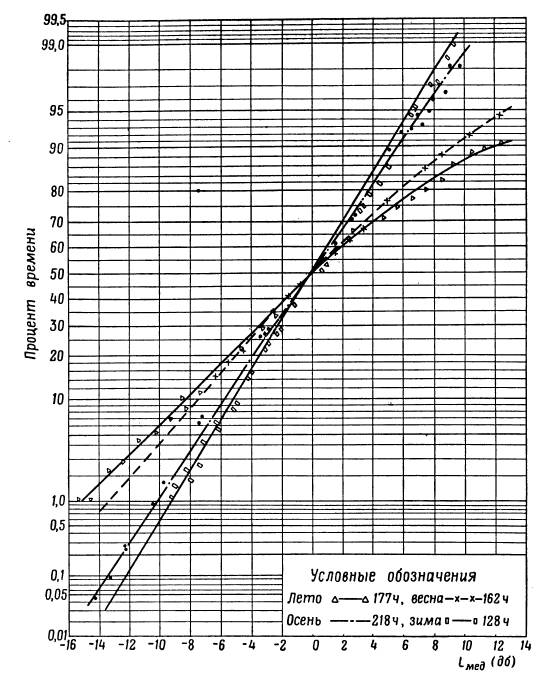
Рис. 5. Распределение медленных (за час) замираний уровня сигнала при дальности связи 150 – 200 км и λ=8,2 см. Имеется также экспериментально снятая зависимость средних значений величины стандартного отклонения σ в зависимости от протяженности трассы, показанная на рис. 6.

Рис. 6. Изменения средних значений величины стандартного отклонения в зависимости от протяженности трассы Величину потерь от медленных замираний рекомендуется определять по графикам логарифмически нормального закона, изображенным на рис. 7 [1], которые близки к экспериментальным, для чего значения σ следует определять из рис.6, а Р1%=1-Р%, где Р% – заданное время безотказной работы линии.

Рис. 7. Интегральные функции распределений амплитуд сигналов Примечание: на рис.7 опечатка, надписи σ=5 дБ и σ=10 дБ нужно поменять местами. Для расчетов на ПЭВМ нужно получить формулы, по которым строятся графики для логарифмически нормального закона распределения, приведенные на рис. 7, причем для любых значений σ. Обратим внимание на то, что для этих графиков, отклонениям от медианного значения на величину σ (5 дБ и 10 дБ соответственно) соответствует % времени, равный 84%, то есть вероятность 0.84. При логарифмически нормальном законе нормальному распределению подчиняется не сама случайная величина, а ее логарифм. При логнормальном распределении плотность распределения вероятности записывается формулой [8]:

(2.18) а функция распределения рассчитывается по формуле

(2.19) где σ – величина стандартного отклонения; μ – смещение;


(2.20)


(2.21) Глубина замираний при логарифмически нормальном законе распределения определяется двумя параметрами: вероятностью F(Х), изменения уровня сигнала по отношению к медианному уровню, и величиной стандартного отклонения σ. Значение σ находим по рис 6. При нахождении значений σ для весны и осени будем считать, что это средние значения между значениями для зимы и для лета. Аппроксимация приведенных на рис. 6 графиков дает следующие формулы для вычисления σ:

(2.22)

(2.23)

(2.24) На рис. 7а показаны четыре функции логарифмически нормального распределения для значений стандартного отклонения σ=1дБ (красная линия), σ=5дБ (синие точки), и σ=10дБ (линии фиолетового и зеленого цвета). Примечание: Построение графиков выполнено в программе Matcad, слева от графиков показаны расчетные формулы. Для примера показаны два типа расчетных формул (через функцию pnorm и функцию erf), дающих одинаковый результат.
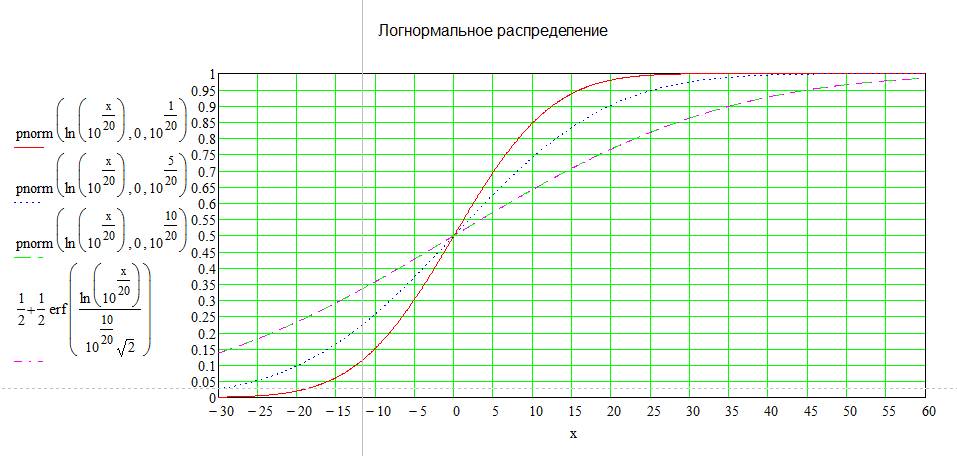
Рис. 7а. Интегральные функции распределений амплитуд сигналов при логнормальном распределении. Ось Х – децибелы по отношению к медианному значению. Ось Y – вероятность не превышения величины Х.
Характеристики логарифмически нормального закона, приведенные на рис.7, не соответствуют полученным интегральным функциям стандартного логнормального распределения рис.7а. Характеристике для σ=10 на рис .7 соответствует характеристика для σ=1 на рис. 7а. Нужно привести расчетные характеристики в соответствие с характеристиками рис.7, так как они близки к экспериментальным, таким образом, чтобы отклонение от медианного значения равное σ соответствовало значению интегральной функции 0.84, как на графиках рис 7. Проведенные расчеты показали, что для получения расчетных характеристик, близких к экспериментальным, при расчете по формуле (2.23) нужно вместо значений σ, полученных из рис.6, применять значения σ1, в соответствии с таблицей 1.

Данные таблицы 1 могут быть аппроксимированы формулой:

(2.25) Интегральные функции распределений амплитуд сигналов при логнормальном распределении, рассчитанные с учетом таблицы 1 для значений σ равных 3дБ, 5дБ, 7дБ, 10дБ (соответственно σ1 равных -9,5дБ, -5дБ, -2дБ, 1дБ), показаны на рис 8.
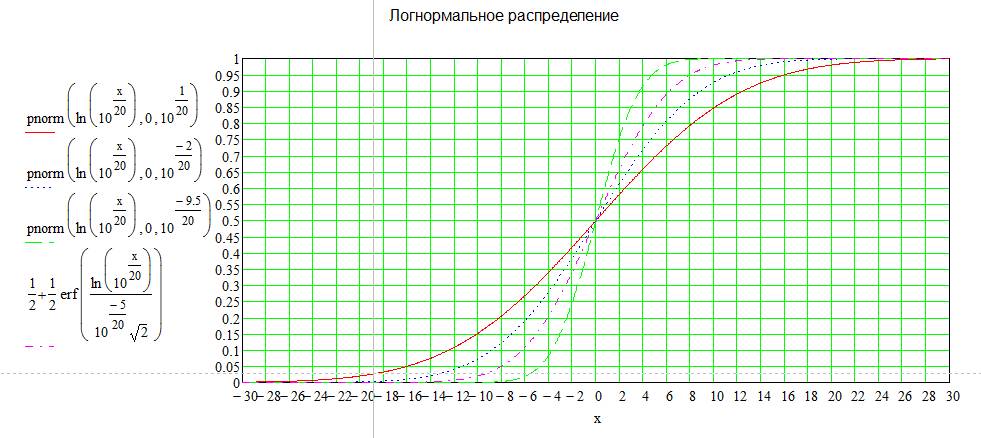
Рис. 8. Интегральные функции распределений амплитуд сигналов при логнормальном распределении
Полученные расчетные характеристики близки к экспериментальным. Потери от медленных замираний Lмз, определяются как отклонение сигнала от медианного значения, для заданной вероятности (заданного % времени безотказной работы). Поскольку отношение амплитуд сигналов и отношение мощностей сигналов, выраженные в децибелах, равны, то эти характеристики можно применять как для определения замираний амплитуды сигнала, так и для замираний мощности сигнала. 2.2.2.2 Потери Lз для телефонного канала. Для того чтобы найти величину Lз, соответствующую определенной надежности связи при работе в телефонном режиме за продолжительный период (месяц), нужно найти функцию результирующего распределения уровня сигнала, учитывающую как быстрые, так и медленные замирания. Она будет зависеть от величины стандартного отклонения логарифмически нормального распределения σ для данной протяженности радиолинии и данного сезона года, а также от кратности разнесения. Из рис.6 находим среднее значение величины стандартного отклонения σ (дБ) в зависимости от протяженности трассы. В зависимости от кратности разнесения по одному из рисунков 9 – 11 находим потери, обусловленные влиянием быстрых и медленных замираний в соответствии с заданной надежностью связи и найденным σ (дБ).

Рис. 9. Потери, обусловленные влиянием быстрых и медленных замираний, при одинарном приеме

Рис. 10. Потери, обусловленные влиянием быстрых и медленных замираний, при сдвоенном приеме

Рис. 11. Потери, обусловленные влиянием быстрых и медленных замираний, при счетверенном приеме
Линии на рисунках 9 – 11 можно аппроксимировать формулой

(2.26) где х – надежность связи в %. Коэффициенты аппроксимации a, b, c для целых значений σ, в зависимости от вида приема, приведены в таблице 2.
Таблица 2. Коэффициенты для формул аппроксимации

Получить обобщенные формулы аппроксимации в зависимости от σ не представляется возможным, так как не просматривается зависимость коэффициентов аппроксимации от σ. Поэтому для вычисления Lз(дБ) при дробных значениях σ придется делать линейную интерполяцию между значениями Lз(дБ), вычисленными для соседних целых значений σ. Для этой цели можно применять формулу: Lз(дБ)=Lз(дБ,σцел)+(Lз(дБ,σцел+1)-Lз(дБ,σцел))×σдр, (2.27) где σцел – целая часть значения σ; σдр – дробная часть значения σ; Lз(дБ,σцел) – значение Lз(дБ), вычисленное для целой части значения σ; Lз(дБ,σцел+1) – значение Lз(дБ), вычисленное для σ на 1 больше его целой части. 2.2.3 Потери Lp, обусловленные влиянием неровностей рельефа местности. Эти потери рекомендуется определять по графику рис. 12. Определяем значение Δ для трассы,

(2.28) где θсум= θпер + θпр, – углы горизонта со стороны передатчика и приемника; Δ и θ – в градусах; hа – высота подъема передающей и приемной антенн в метрах.

Рис. 12. Зависимость потерь, обусловленных влиянием неровностей рельефа, от суммарного угла закрытия Кривые рис. 12 можно аппроксимировать формулой: Lp(дБ)=a×ebΔ+c×edΔ, (2.29) где a, b, c, d – коэффициенты, зависящие от дальности связи R, приведены в таблице 3. Таблица 3. Коэффициенты аппроксимации

Если дальность связи совпадает с табличными значениями, то значение Lp(дБ) вычисляется непосредственно по формуле (2.33) с использованием коэффициентов из таблицы 3. Если дальность связи не совпадает с табличным значением, то для промежуточных значений необходимо вычислить табличные значения Lp(дБ) для нижнего Rн и верхнего Rв табличных значений дальности связи относительно заданной дальности связи R, и провести линейную интерполяцию полученных значений. Значение Lp(дБ) для дальности связи R будет определяться по формуле:

(2.30) 2.2.4 Потери Lh, обусловленные влиянием земной поверхности при малых величинах отношения h/λ, рекомендуется находить по графику рис. 13.

Рис. 13. Зависимость потерь от отношения высоты антенны к длине волны для различных расстояний Кривые, показанные на рис. 13 могут быть аппроксимированы формулой

(2.31) где х=h/λ; a1, b1, c1, a2, b2, c2 – коэффициенты, зависящие от дальности связи R, приведены в таблице 4. Таблица 4. Коэффициенты аппроксимации

Если дальность связи совпадает с табличными значениями, то значение Lh(дБ) вычисляется непосредственно по формуле (2.34) с использованием коэффициентов из таблицы 4. Если дальность связи не совпадает с табличным значением, то для промежуточных значений необходимо вычислить табличные значения Lh(дБ) для нижнего Rн и верхнего Rв табличных значений дальности связи относительно заданной дальности связи R, и провести линейную интерполяцию полученных значений. Значение Lh(дБ) для дальности связи R будет определяться по формуле:

(2.32) 2.2.5 Потери усиления антенн Lа(дБ). Существует два различных понимания природы потери усиления антенн при больших коэффициентах усиления антенн. В [1] формула для расчета этих потерь выведена исходя из уменьшения объема переотражения в тропосфере при уменьшении диаграммы направленности антенн. В [2] формула получена исходя из того, что при больших размерах антенны распределение фаз в раскрыве антенны при приходе волн с различных направление будет отличаться от прихода плоской волны [7]. Результат вычислений La по формуле из источника [1] значительно отличается от экспериментальных данных по этому параметру, приведенных в источниках [1] и [7], а результат вычислений по формуле из источника [2] совпадает с этими экспериментальными данными. Поэтому потери усиления антенны будем определять по формуле из источника [2]. Определим потери усиления антенны: Lа(дБ) = 0,07×exp [0,055× (Gпер + Gпр)], (2.33) где Gпер и Gпр − коэффициенты усиления антенны (дБ).
2.2.6 Климатические потери Lк. Это потери, связанные с отличием климатических особенностей района размещения станций от климатических условий центральной части ETC, можно оценить на основе установленной связи между потерями и значением коэффициента преломления у земной поверхности Nз. По данным многолетних измерений метеорологических элементов, проводившихся на территории СССР, были рассчитаны значения Nз и вычислены величины Lк. На рис. 14 и 15 показаны изолинии изменения величины потерь Lк на территории СССР. Значения Lк даны на картах для трасс длиной 100, 200 и 300 км.

Рис. 14. Изменения потерь, обусловленных климатическими особенностями различных районов (январь, расстояния 100, 200 и 300 км)

Рис. 15. Изменения потерь, обусловленных климатическими особенностями различных районов (июль, расстояния 100, 200 и 300 км)
2.3 Общие потери на трассе. Общие потери определяются по формуле: L(дБ)=L0(дБ)+Lдоп(дБ). (2.34) При необходимости перехода от среднемесячной оценки к среднесуточной или среднегодовой, необходимо подкорректировать общие потери на трассе, определив величину Δδ из рис. 16.

Рис. 16. Зависимость дополнительного запаса высокочастотного уровня сигнала от расстояния при переходе от суточной надежности к месячной или годовой надежности L(сут) = L(мес)+Δδ (мес). (2.35) L(год) = L(сут)-Δδ (год)=L(мес)+Δδ (мес)-Δδ (год). (2.36) Кривую для годовой надежности (рис.16) можно аппроксимировать формулой:
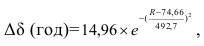
(2.37) А для месячной

(2.38) 2.4 Мощность шума на входе приемника. 2.4.1 Для телеграфных видов работы определяем мощность шума на входе приемника с учетом скорости передачи. Рш.пр = Fэ×К×Т0×Δf(Гц) = 4×10-21×Fэ×Δf. (2.39) Для различных типов модуляции ширина спектра сигнала Δf определяется: – при непосредственной модуляции несущей для амплитудной и фазовой манипуляции Δf=1/Тс=V, где Тс – длительность импульса; – V(бод) – скорость передачи информации. – для частотной манипуляции Δf=V при m≤1, где m=fд/F – индекс частотной модуляции, где fд – девиация частоты, F – частота манипуляции. При m>1, Δf=2 fд=fр, где fр – разнос частот.
Для амплитудной, фазовой и узкополосной частотной манипуляции при непосредственной модуляции несущей формулы будут иметь вид: Рш.пр =4×10-21×Fэ×V. (2.40) Рш.пр(дБ)=10lg(Рш.пр). (2.41) Fэ(дБ)=10lg(Fэ). (2.42) 2.4.2 В телефонном режиме надежность и качество связи на радиолинии оцениваются по отношению мощности сигнала к мощности шума на выходе оконечной станции (точнее, в такой точке телефонного канала, в которой уровень сигнала равен 0 дБ/мВт, т.е. Рс=1 мВт). Для рассматриваемых многоканальных радиолиний с частотной модуляцией и частотным уплотнением мощность шума в телефонном канале определяется в точке с нулевым относительным уровнем сигнала Рс.т=0 дБ/Вт, т.е. в условной точке с уровнем сигнала 1 мВт. Воспользоваться формулой для определения мощности шума в телефонном канале Рш.т. из источника [1] не удалось, так как не указаны единицы измерения входных параметров, а попытка подбора единиц измерений к успеху не привела. Кроме того, появилось подозрение о наличии в формуле опечатки, так как размерность вычисляемого значения Рш.т. не соответствует ватам. Для вывода достоверной формулы вычисления мощности шума в телефонном канале воспользуемся данными из источника [4]. Так как ширина полосы телефонного канала много меньше средней частоты канала в линейном спектре ΔFк˂˂Fк, то спектральную плотность шумов в полосе одного канала можно считать постоянной. Тогда квадрат эффективного напряжения шумов в канале можно представить в виде:

(2.43) где ΔFk=3100 Гц – ширина полосы пропускания телефонного канала; Fк – средняя частота телефонного канала в линейном спектре аппаратуры уплотнения; σ2=Рш/Δf – спектральная плотность шума на входе приемника в полосе 1 Гц; uc – эффективное напряжение сигнала на входе приемника; с – коэффициент пропорциональности между отклонением частоты и напряжением на выходе канала: Uк=с×Δfк, (2.44) где Uк – эффективное напряжение сигнала на выходе канала; Δfк – эффективная величина отклонения частоты на один канал, равна удвоенной девиации частоты. Тогда можно записать:

(2.45) где Рш=FэkTΔf – мощность шума на входе приемника; Рвх – мощность сигнала на входе приемника; Δf – ширина полосы приемника; Fэ – эффективный коэффициент шума приемника; k=1,38×10-23 дж/град – постоянная Больцмана; Т=290о k (20о C) – абсолютная температура среды.
Подставляя (2.45) в (2.43) и значение «с» из (2.44) в (2.43) получим:
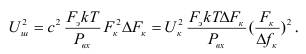
(2.46) Перейдем к псофометрической мощности шума на выходе канала: Рш.т=Кп2×Uш2/Rк, (2.47) где Кп – псофометрический коэффициент (Кп=0,75 при ΔFk=3100 Гц); Rк – сопротивление нагрузки канала; Подставляя (2.48) в (2.49) получим:

(2.48) где Uк2/Rк=Рвых.т=10-3 Вт – мощность сигнала на выходе телефонного канала (в условной точке, в которой рассчитывается псофометрическая мощность шума); Рвх—мощность сигнала на входе приемника (Вт).
Эта формула справедлива и для малого числа каналов n (практически для n≥2). Из нее следует, что тепловые шумы при постоянных параметрах аппаратуры целиком определяются мощностью принимаемого сигнала. Так же как уровень принимаемого сигнала, мощность тепловых шумов на выходе линии является случайной функцией времени. Для подвижный войсковых тропосферных станций телефонный канал считается нормальным если отношение сигнал/шум на выходе телефонного канала (в точке, где Рвых.т=10-3 Вт) будет не менее 35 дБ.
2.5 Требуемое превышение мощности сигнала над мощностью шума Этот параметр определяется для обеспечения требуемой вероятности ошибки Рош с учетом релеевских замираний. В течение времени сеанса связи потери на трассе могут изменяться только за счет быстрых замираний. Поэтому величину необходимого превышения сигнала над шумами «В» следует определять как требуемое отношение сигнал/шум для получения вероятности Рош не меньше заданной, найденное с учетом кратности разнесения каналов приема. В=h02треб. Вероятность битовой ошибки зависит от вида модуляции и вида приема (когерентный, некогерентный). h02треб будем определять для некогерентного приема: а) Для случая амплитудной манипуляции вероятность битовой ошибки определяется по формуле:

(2.49) где h02 –отношение сигнал/шум на входе детектора, n – кратность разнесения. Требуемое превышение сигнала над шумом В, необходимое для обеспечения заданной достоверности приема, будет равно h02, найденному из (2.48):

(2.50) б) Для случая частотной манипуляции вероятность битовой ошибки определяется по формуле:

(2.51)
(2.52)
в) Для случая относительной фазовой манипуляции вероятность битовой ошибки определяется по формуле:

(2.53)
(2.54)
В(дБ)=10×lgВ. (2.55) 2.6 Максимально допустимое значение полных потерь. Параметр определяется по формуле: Lп.пред(дБ)=Рпер(дБ)-Рш.пр(дБ)-В(дБ). (2.56) 2.7 Мощность сигнала на входе приемника. Определяется по формуле: Рвх(дБ)=Рпер(дБ)-L0(дБ)– Lдоп(дБ). (2.57) 2.8 Энергетический запас выбранной трассы. Для наихудшего зимнего месяца энергетический запас выбранной трассы можно считать по следующей формуле: δ(дБ)=Lп.пред(дБ)-L(дБ). (2.58) При пересчете к суточной или годовой надежности следует воспользоваться формулами, аналогичными (2.37) и (2.38). δ (сут) = δ (мес)-Δδ (мес). (2.59) δ (год) = δ (сут)+Δδ (год)= δ (мес)-Δδ (мес)+Δδ (год). (2.60) 2.9 Приближенная оценка максимальной дальности связи. Вычисляются постоянные потери, величина которых не зависит от дальности связи: Lпост=Lдоп-Lмед.(дБ). (2.61) Вычисляется коэффициент пропорциональности между реальными потерями в свободном пространстве и потерями в линии, зависящими от дальности связи: K=L0/(L-Lпост), (2.62) если энергетический запас трассы δ(дБ)<3дБ, величину К уменьшить в 2 раза для повышения точности вычислений.

(2.63) где λ – длина волны в см. Расчет проводится методом последовательного приближения. В разработанной программе рассчитанное значение Rпред на следующем цикле автоматически вводится в программу как заданная дальность связи и расчет повторяется до тех пор пока энергетический запас трассы не будет в пределах 1< δ(дБ)<0,5. Полученное при этом условии Rпред и считается предельной дальностью связи. 3. Расчет по методике, изложенной в рекомендациях МСЭ-R P.617. По данной методике определяются потери для худших условий при заданной дальности связи и распространении за счет рассеяния на неоднородностях тропосферы [2]. По эмпирическим формулам определяются среднегодовые медианные потери, не превышаемые в течение более чем q% времени, больших 50%.
3.1 Из рис. 17 находим климатическую зону, в которой работает линия связи. Вся территория России входит в 5-ю зону.

Рис. 17. Классификация климатических зон 3.2 Для выбранной климатической зоны из таблицы 5 находим метеорологический параметр и параметры структуры атмосферы, М и γ, а также номер уравнения, которое нужно использовать при расчетах. Для пятой зоны М=29,73 дБ, γ=0,27 км-1, уравнение(3.8).
Таблица 5 – Значения метеорологических параметров и параметров структуры атмосферы

3.3 Вычисляем угол рассеяния по формуле: θ(мрад)=θe+θпер+θпр, (3.1) где θпер(мрад) и θпр(мрад) − углы горизонта со стороны передатчика и приемника, соответственно, а θe(мрад) = R×103/(k×Rз) мрад=0,012×R, (3.2) где: R – длина трассы (км); Rз – радиус Земли, равный 6370 км; k – коэффициент эквивалентного радиуса Земли. Для средних условий рефракции (следует использовать значение k = 4/3, если нет более точных данных). Примечание: Поскольку в исходных данных θпер и θпр заданы в градусах, потребуется их пересчет в мрад.

(3.3) 3.4 Определяем потери передачи LN, в зависимости от высоты общего объема по формуле: LN(дБ) = 20×lg(5 + γ H) + 4,34×γ×h, (3.4) где H(км) = 10–3×θ×R/4; (3.5) h(км) = 10–6×θ2×k× Rз /8; (3.6) γ − параметр структуры атмосферы, определенный в пункте 3.2. 3.5 Определяем параметр ds – эквивалентное расстояние (используется в некоторых формулах для вычисления Y(90) ds(км) = θ×k×Rз/1000=8,4933×θ, (3.7) где k=4/3 – коэффициент эквивалентного радиуса Земли. 3.6 Вычисляем коэффициент преобразования Y(90) (дБ) для времени q=90% по формуле: Y(90) = -2,2-[8,1-2,3×10-4×min(1000×f, 4000)]×exp(-0,137×h) (3.8) Y(90) = -9,5-3×exp(-0,137×h) (3.9) Y(90) = -8,2 ds < 100 (3.10а) Y(90) = 1,006×10-8×ds3 -2,569×10-5×ds2+0,02242×ds -10,2 100≤ ds<1000(3.10б) Y(90) = -3,4 в иных случаях (3.10в) Y(90) = -10,845 ds<100 (3.11а) Y(90) = -4,5×10-7×ds3+4,45×10-4×ds2-0,122×ds-2,645 100≤ ds<550 (3.11б) Y(90) = -8,4 в иных случаях (3.11в) Y(90) = -11,5 ds<100 (3.12а) Y(90) = -8,519×10-8×ds3+7,444×10-5×ds2+4,18×10-4×ds-12,1 100≤ ds<465(3.12б) Y(90) = -4,0 в иных случаях (3.12в) 3.7 По таблице 6 определяем коэффициент C(q) для искомого процента времени не превышения q. Таблица 6 Зависимость C(q) от q

Эти табличные данные могут быть представлены кривой, изображенной на рис. 18.
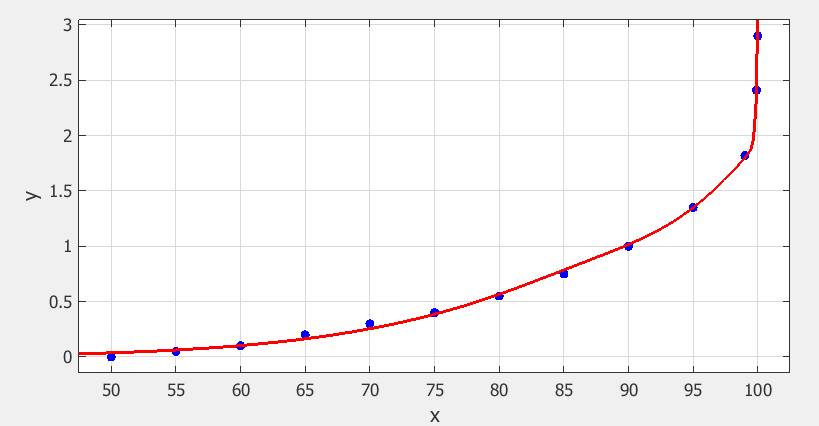
Рис. 18. Аппроксимация данных таблицы 6 Кривая, изображенная на рис. 18 может быть аппроксимирована следующей формулой:

(3.13) с коэффициентами: a1=1.473e14 a2=-0.2272 a3=9.047
b1=108.8 b2=95.58 b3=153.3
c1=1.534 c2=7.786 c3=44.08. 3.8 Определяем коэффициент преобразования, Y(q) (потери от замираний), для процента времени не превышения q, отличного от 50%, по формуле: Y(q)=C(q)×Y(90) дБ. (3.14) 3.9 Определяем потери между антеннами и средой распространения, La: La=0,07×exp[0,055×(Gпер+Gпр)] дБ, (3.15) где Gпер и Gпр − коэффициенты усиления антенн. 3.10 Определяем среднегодовые потери передачи, не превышаемые для процента времени q% по формуле: L(q)=M+30×lg(fр)+10×lg(R)+30×lg(θ)+LN+La-Gпер-Gпр-ηпер-ηпр-Y(q). (3.16) 3.11 Определяем медианные потери в наихудший зимний месяц для процента времени q%. 3.11.1 Определяем эквивалентное расстояние по формуле: dq(км)=R+8,5×(θпер(мрад)+θпр(мрад)). (3.17) 3.11.2 По графикам рис.19 определяем разность потерь между среднегодовыми распределениями и распределениями для среднего наихудшего месяца ΔL.

Рис. 19. Кривые разности между основными потерями передачи для наихудшего месяца и годовыми основными потерями передачи
Кривые, показанные на рис. 19 можно аппроксимировать формулой: ΔL(дБ)=p1×dq2+p2×dq+p3, (3.18) где p1, р2, р3 – коэффициенты аппроксимации, зависящие от q, приведены в таблице 7 для применяемых на практике значений q.
Таблица 7. Коэффициенты аппроксимации

3.11.3 Определяем медианные потери за средний наихудший зимний месяц по формуле: Lм(мес)=L(q)+ΔL (дБ). (3.19) 3.12 При переходе к суточной надежности воспользуемся формулами (2.35) и (2.38) из первой методики. Определяем средние медианные потери за сутки: Lм(сут) = Lм(мес)+Δδ (мес). (3.20)

(3.21) 3.13 Общее затухание на линии будет определяться по формуле: L=Lм+Lбз (дБ), (3.22) где Lм – соответствующее значение L(q), Lм(мес) или Lм(сут), в зависимости от заданного периода оценки надежности; Lбз – потери от быстрых (релеевских) замираний, определяемые в п.2.2.1.1.1. 3.14 Определяем мощность сигнала на входе приемника: Рвх(дБ) = Рпер(дБ)-L(дБ). (3.23) 3.15 Переводим полученное значение Рвх(дБ) в Рвх(Вт) Рвх(Вт)=10Рвх(дБ)/10 и находим отношение сигнал/шум на входе приемника: h02= Рвх(Вт)/ Рш.пр. (3.24) Поскольку все каскады приемника от входных цепей до детектора являются линейными, при непосредственной модуляции несущей это же отношение сигнал/шум будет и на входе детектора, поэтому по нему можно определять вероятность битовой ошибки. При передаче битовой информации по одному из телефонных каналов связи, входным сигналом для детектора является выходной сигнал телефонного канала, поэтому отношение сигнал/шум на входе детектора будет таким же, как на выходе телефонного канала: h02=1мВт/Рш.т, (3.25) где Рш.т – мощность шума на выходе телефонного канала, определяемая по формуле (2.50). Расчеты h02, проводимые на основе двух рассмотренных выше методик, показали, что результаты расчетов не всегда совпадают. При небольших дальностях связи, примерно до 130 км, результат расчета по первой методике будет больше результата по второй методике, затем результаты совпадают, а при дальностях больше 150 км – результаты расчета по второй методике будут больше, чем по первой. Какая из методик дает более точный результат сказать сложно, поэтому, на наш взгляд, при расчете тропосферных трасс, расположенных на территории бывшего СССР, целесообразно использовать среднее значение h02, от рассчитанных по двум этим методикам.
3.16 Определение длительности замираний В некоторых случаях, особенно при моделировании замираний, требуется знать длительность замираний. В соответствии с [11] длительность релеевских замираний будем определять по формуле:
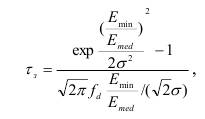
(3.26) где Emin/Emed – глубина быстрых замираний по отношению к медианному значению. Определяется для заданной надежности связи в соответствии с
п. 2.2.1.1.1; σ – среднеквадратическое отклонения глубины замираний, для графика, по которому определялась глубина замираний σ=0,84; fd=V/λ – доплеровский сдвиг, где V – относительная скорость движения переотражающего объекта (м/сек), в данном случае скорость ветра в объеме рассеяния тропосферы; λ – длина волны несущего излучения (м).
3.17 Оценка качества радиоканала Оценку качества радиоканала будем производить по вероятности битовой ошибки в условиях белого гауссова шума, при отсутствии помехоустойчивого кодирования. Вероятность ошибки с учетом используемого вида модуляции находим по формуле [5]:

(3.27)

m – коэффициент, зависящий от вида модуляции и типа модулирующего сигнала. m=0,5 для АМ, m=1 для ЧМ, m=2 для ФМ.

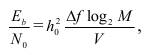
(3.28) где Eb – энергия на 1 бит; N0 – спектральная плотность мощности шума; М – количество уровней модуляции; Δf – полоса пропускания входного фильтра. При ЦОС обычно применяется цифровой фильтр с Δf=V; V – битовая скорость передачи информации. При условии применения такого цифрового фильтра уравнение (3.28) можно записать в виде:

(3.29) В условиях белого гауссова шума для случайной бинарной величины, которая может принимать два различных значения и априорная вероятность передачи каждого их этих значений 1/2, полная вероятность ошибочного приема в общем виде определяется по формуле [5]:

(3.30)

Е – энергия разностного сигнала; N0 – спектральная плотность мощности шума. Для многоуровневой модуляции вероятность ошибочного приема будет определяться по формуле:

(3.31) где М – количество уровней модуляции. При переходе к энергии на бит получаем формулу:

(3.32)
При вычислении в Mathcad интеграл вероятности
 вычисляется по формуле
вычисляется по формуле

(3.33) 4. Оценка качества радиоканала тропосферной связи при различных видах модуляции для когерентного и некогерентного приема 4.1 Непосредственная передача прямоугольных импульсов: – биполярные прямоугольные импульсы:
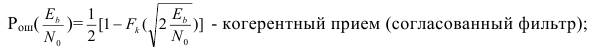
(4.1)

(4.2) где Ts – длительность символа; В – ширина полосы пропускания ФНЧ. Обычно применяются ФНЧ с полосой пропускания в 2 раза превышающей частоту Найквиста В=1/Ts. Поэтому все формулы для некогерентного приема приведены для случая применения именно такого ФНЧ. – однополярные прямоугольные импульсы:
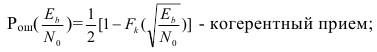
(4.3)

(4.4) 4.2 Амплитудная манипуляция: а) аналоговая обработка сигнала [10]: – когерентный прием (фазовый детектор)

(4.5) – некогерентный прием (амплитудный детектор)

(4.6) где Тс – длительность импульса; ΔFс – ширина спектра сигнала. При импульсах типа «меандр», Тс×ΔFс=1. Тогда

(4.7) б) цифровая обработка сигнала [5]: – однополярные прямоугольные импульсы:

(4.8)

(4.9)

(4.10)

(4.11)

– биполярные прямоугольные импульсы:

(4.12)

(4.13)

(4.14)

(4.15) 4.3 Частотная манипуляция: а) аналоговая обработка сигнала [5]: – оптимальный прием (когерентный прием)

(4.16) – квазиоптимальный прием (некогерентный прием)

(4.17) б) цифровая обработка сигнала [5]: – FSK с разрывом фазы, с ФНЧ:

(4.18) – MSK без разрыва фазы, с ФНЧ:

(4.19) – при минимальном отклонении фазы на π/2 (при индексе модуляции m=1/2):

(4.20) – многоуровневый сигнал:

(4.21) 4.4 Фазовая манипуляция [8]: а) аналоговая обработка сигнала [10]: – оптимальный когерентный прием

(4.22) б) цифровая обработка сигнала [5]: – оптимальный когерентный прием

(4.23) – квазиоптимальный прием:

(4.24) – многоуровневый ФМ сигнал:
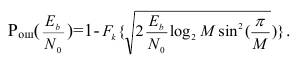
(4.25) 4.5 Относительная фазовая манипуляция: а) аналоговая обработка сигнала [10]: – сравнение фаз
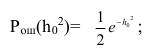
(4.26) – сравнение полярностей

(4.27) 4.6 Технология OFDM: Помехоустойчивость OFDM системы для канала Релея определяется выражением [6]:

(4.28) где М – количество поднесущих в сигнале OFDM.
Последние комментарии
2 часов 22 минут назад
18 часов 26 минут назад
1 день 3 часов назад
1 день 3 часов назад
3 дней 9 часов назад
3 дней 14 часов назад