Истина в пределе. Анализ бесконечно малых [Антонио Дуран] (fb2) читать онлайн
[Настройки текста] [Cбросить фильтры]
[Оглавление]
Антонио Дуран
ИСТИНА В ПРЕДЕЛЕ.
Анализ бесконечно малых
Предисловие
Анализ бесконечно малых, вне всяких сомнений, наиболее мощное и эффективное средство изучения природы, когда-либо созданное математиками. Эта дисциплина зародилась в древности и развивалась очень долго. С III века до н. э., когда Архимед впервые использовал бесконечно малые величины для вычисления площади, до эпохи Ньютона и Лейбница, которые придали окончательный вид анализу бесконечно малых, прошло почти две тысячи лет. Но лишь спустя еще полтора столетия Коши и Вейерштрасс «приручили» бесконечно малые величины, найдя им адекватное логическое объяснение. Если оставить мистические свойства бесконечности в стороне, то анализ бесконечно малых в том виде, в каком он существует сегодня, образован двумя внешне различными направлениями: дифференциальным исчислением, в основе которого лежит понятие производной, и интегральным исчислением. Их объединяет основная теорема анализа, согласно которой дифференцирование и интегрирование являются взаимно обратными операциями. Анализ бесконечно малых находит очень широкое применение ввиду того, что производные и интегралы используются во множестве областей математики, физики, техники, экономики и других наук. К примеру, производная — это фундаментальное понятие физики, так как ему соответствуют такие понятия, как мгновенная скорость и мгновенное ускорение, а следовательно, и понятие силы. Неудивительно, что большинство физических законов выражены в виде дифференциальных уравнений, где производные используются наравне с обычными функциями. Приведем еще один из множества примеров, показывающих, насколько разными способами может применяться анализ бесконечно малых. Кому из нас, привыкших к современному медицинскому оборудованию, не делали магнитно-резонансную томографию (МРТ)? Когда волна проходит сквозь наше тело, ее поведение можно описать интегралом, значение которого равно разности интенсивности волны на входе и выходе из нашего организма. Аппарат «угадывает», что находится внутри нашего тела, на основании значений всех этих интегралов. Современная физика родилась во времена Ньютона, который, помимо прочего, был создателем анализа бесконечно малых. Это совпадение не случайно: по словам самого Ньютона, идеи, которые окончательно оформились с открытием его метода исчисления, родились одновременно с первыми представлениями о гравитации. Первая, рудиментарная версия анализа бесконечно малых должна была помочь Ньютону на основе законов Кеплера о движении планет вывести закон гравитации, согласно которому сила притяжения тел обратно пропорциональна квадрату расстояния между ними. Нечто подобное произошло, когда новая версия анализа бесконечно малых была создана усилиями Лейбница. Вскоре после того как в 1684 и 1686 году были опубликованы две его статьи, в которых излагались основы нового исчисления, оно было успешно применено для решения множества разнообразных задач механики, которые до этого не могли решить даже гениальные Леонардо да Винчи и Галилей. Речь идет о задаче о цепной линии, задаче о брахистохроне и некоторых других. Об анализе бесконечно малых и его удивительной истории и пойдет речь в этой книге.Глава 1. Что такое анализ бесконечно малых и для чего он нужен
Анализ бесконечно малых — это область математики, которая имеет огромное значение для науки и техники. Чтобы понять, из чего состоит эта сложная и тонкая дисциплина, наверное, следует начать с рассказа о задачах, которые решаются с ее помощью. Так читатель сможет понять, насколько важен и широко распространен анализ бесконечно малых в современной науке и технике. Эти задачи могут существенно различаться между собой. Так, к ним относятся физическая задача на определение скорости тела при известном пройденном расстоянии и обратная ей задача, в которой нужно рассчитать пройденный телом путь, зная его скорость. С помощью этого же анализа решаются задачи, в которых требуется, например, вычислить скорость автомобиля, зная силу тяги его двигателя, или определить положение гитарной струны после того, как за нее потянули. Также существуют и геометрические задачи, в частности о расчете угла наклона касательной, длины кривой или площади криволинейной фигуры. Многие задачи, решаемые с помощью бесконечно малых, лежат на стыке физики и инженерного дела, например, задача об определении центра тяжести тела (что крайне важно при постройке кораблей), о вычислении положения кабеля, висящего между двумя столбами (эта задача решается при прокладке воздушных линий электропередачи), о расчете распределения температуры на различных участках нагреваемой металлической пластины, об определении движения жидкостей (эта задача играет большую роль в авиационной промышленности и других отраслях) и многие другие. Этот список можно продолжать практически бесконечно. Именно бесконечно малые величины являются основным предметом изучения анализа бесконечно малых. Понятие бесконечности придает анализу бесконечно малых удивительную мощь, подчас граничащую с волшебством. Бесконечность — это основа математического анализа, но чтобы осознать, насколько велика ее роль, сначала следует уделить несколько абзацев основным понятиям исчисления. Как уже говорилось в предисловии, анализ бесконечно малых состоит из двух внешне различных направлений: дифференциального и интегрального исчисления, каждое из которых имеет свои понятия и методы. В дифференциальном исчислении рассматриваются задачи о вычислении угла наклона касательной к кривой и расчета скорости при известном пройденном пути. К интегральному исчислению относятся задачи о вычислении площадей и объемов, а также задачи расчета пройденного пути при известной скорости. Фундаментальным понятием дифференциального и интегрального исчисления является понятие функции.Функции
Большинство изучаемых нами процессов, будь то природные, экономические или любые другие, можно смоделировать с помощью функций, а затем проанализировать математическими методами. Иными словами, функции — это язык, который используется в науке при изучении всех этих процессов. Функция — это правило, сопоставляющее одному числу другое. Обычно (но не всегда) это правило выражается с помощью алгебраических операций над числами. Так, функция может сопоставлять одному числу (обозначим его t) другое число по следующему закону:(t2 + 1)/(t4 + 5)
Так как число t может принимать различные значения, его называют переменной. Как правило, функции обозначаются буквами f, g, h, s или v, переменные — буквами x, у, z или t. Значение, которое функция сопоставляет произвольному числу t, записывается как f(t). Предыдущий пример будет выглядеть так:f(t) = (t2 + 1)/(t4 + 5)
В частности, когда мы присваиваем переменной t конкретные значения, мы определяем значения функции. Так, при t = 1 получим:f(1) = (12 + 1)/(14 + 5) = 2/6
при t = 2 имеем:f(2) = (22 + 1)/(24 + 5) = 5/21
В следующей таблице приведены несколько значений переменной и соответствующих им значений функции:t …… F(t)
-1 …… 2/6
0 …… 1/5
√2 …… 3/9
Простейшая физическая система — это движущееся тело. Его перемещение можно описать функцией s, которая сопоставляет каждому моменту времени t путь s(t), пройденный телом, или функцией v, которая сопоставляет каждому моменту времени t скорость v(t), с которой движется тело. Рассмотрим конкретный пример. Если тело по истечении t секунд преодолело путь, точно равный квадратному корню из t метров, функция, описывающая это расстояние, будет выглядеть так: s(t) = √t. Эта функция, определяющая пройденный телом путь, также содержит информацию о том, с какой скоростью перемещается тело. Однако, чтобы получить доступ к этой информации, потребуется применить методы дифференциального исчисления. Приведем еще один конкретный пример. Пусть дано тело, которое в течение t секунд двигалось со скоростью, равной t2 м/с. Функция, описывающая скорость движения этого тела, выглядит так: v(t) = t2. Этот пример похож на предыдущий: функция, описывающая скорость движения тела, также содержит информацию о пройденном пути. Однако, чтобы получить эту информацию, необходимо использовать интегральное исчисление. Аналогично с помощью функций можно описать совершенно разные явления: изменение курса акций определенного банка или компании на фондовой бирже, плотность каждого участка тела человека (так мы сможем определить без хирургического вмешательства, где находятся кости, мышцы и внутренние органы) или силу, с которой потоки воздуха воздействуют на крылья самолета во время полета. Чтобы использовать анализ бесконечно малых при решении задач, сначала требуется описать задачу на языке функций. После того как природные, физические или экономические процессы, которые мы хотим изучить, представлены в виде функций, в дело вступают фундаментальные понятия анализа бесконечно малых. С их помощью можно извлечь из функций интересующую нас информацию.Производные
Основное понятие дифференциального исчисления — это понятие производной. В действительности это один из краеугольных камней не только математики, но и науки в целом, ведь за ним скрываются такие фундаментальные понятия, как скорость или сила в физике, угол наклона касательной к кривой в геометрии и многие другие. Производная функции f в точке а показывает, как изменится функция в этой точке по сравнению с тем, как изменяется значение переменной. Рассмотрим две функции из прошлых примеров: s(t) = √t и v(t) = t2. При t = 1 обе эти функции принимают значение 1: s(l) = 1 и v(1) = 1. Однако из таблицы значений видно, что поведение функций вблизи t = 1 существенно различается:t — s(t) — v(t)
0,8 — 0,8944… — 0,64
0,9 — 0,9486… — 0,81
1 — 1 — 1
1,1 — 1,0488… — 1,21
1,2 — 1,0954… — 1,44
Заметьте, что функция v вблизи 1 изменяется более резко, чем функция s. Чтобы измерить эти изменения, то есть чтобы определить производную, выберем произвольное число а и близкое к нему число a + h. Рассмотрим, как изменяется значение функции в этих точках по сравнению с изменением значения переменной. Для этого разделим разность значений функции f(a + h) — f(а) на разность значений переменных, а + h — a = h. Искомая дробь будет иметь вид:(f(a+h) — f(a))/h
Продолжим рассматривать функции s(t) = √t и v(t) = t2. Вычислим значения этой дроби для а = 1: Наибольшее значение этой дроби для функции v приближается к 2, для функции s оно примерно равно 0,5. Это указывает на все тот же факт, который можно видеть из предыдущей таблицы: функция v вблизи точки 1 изменяется быстрее, чем функция s. Нас особенно интересует значение дроби
Наибольшее значение этой дроби для функции v приближается к 2, для функции s оно примерно равно 0,5. Это указывает на все тот же факт, который можно видеть из предыдущей таблицы: функция v вблизи точки 1 изменяется быстрее, чем функция s. Нас особенно интересует значение дроби
(f(a+h)-f(a))/ h
при h = 0, то есть когда числа а + h и а совпадают. Это значение мы назовем производной функции f в точке а. Будем обозначать его f’(а). Это обозначение ввел французский математик Жозеф Луи Лагранж (1736—1813) (см. главу 6). Как можно видеть, значение этой дроби равно 0/0, то есть оно не определено. Однако это лишь кажущаяся неопределенность, поскольку, как показано в предыдущей таблице, для наших функций s(t) = √t и v(t) = t2 при малых значениях h, отличных от нуля, обе дроби(s(l+h)-s(l))/h и (v(1+h) –v(1))/h
определены и равны соответственно 0,5 для функции s(t) = √t и 2 — для функции v(t) = t2. Далее мы покажем, что эти значения действительно соответствуют значениям производных обеих функций в точке 1, то есть s’(l) = 0,5 и v’(l) = 2. Деление ноля на ноль, возникающее при определении производной, представляло трудность для ученых XVII века и их предшественников всякий раз, когда они пытались рассчитать, например, угол наклона касательной к кривой или мгновенную скорость движения тела, зная пройденный им путь. Бесконечность, основа анализа бесконечно малых, скрывается именно в этой операции деления ноля на ноль. Как мы только что сказали, нас интересует значение дроби(f(a+h)-f(a))/ h
при h = 0, когда и числитель, и знаменатель обращаются в ноль. Подобные величины, равные нулю, отношение которых необходимо найти, математики XVII века назвали бесконечно малыми. Анализ бесконечно малых, созданный Ньютоном и Лейбницем и усовершенствованный Леонардом Эйлером (1707—1783) и другими математиками XVIII века, можно назвать искусством манипулирования бесконечно малыми величинами. Как рассказывается в следующих главах, парадоксально, но ни один из этих гениальных математиков не определил сколько-нибудь точно понятие бесконечно малой величины, которое легло в основу математического анализа. Ньютону и Лейбницу удалось завершить работу множества их коллег — математиков XVII века и создать анализ бесконечно малых, одним из разделов которого является дифференциальное исчисление. Ньютон и Лейбниц определили простые правила, позволявшие устранять неопределенность, которая заключается в делении ноля на ноль и возникает всякий раз, когда мы хотим вычислить производную функции. Это были правила вычисления производных элементарных функций, в частности степенной:(xn)′ = nxn-1;
тригонометрических функций:(sin х)′ = cosх, (cos x)′ = -sin х;
логарифмов:(log x)′ = 1/х
показательных функций:(ex)′ = еx
а также правила вычисления производной для основных операции с функциями, в частности суммы:(f+g)′ = f′ + g′;
произведения:(fg)′ = f′g + fg′;
деления:(f/g)’ = (f’g – fg’)/g2
и для сложных функций:(f(g))’ = f’(g)∙g’.
Гордиевым узлом анализа бесконечно малых на протяжении XVII, XVIII и начала XIX века оставалось четкое определение того, как следует понимать значение дроби(f(a+h)-f(a))/h
при h = 0. Этот гордиев узел разрубил французский математик Огюстен Луи Коши (1789—1857), применив понятие предела, которое он сам же и определил более или менее точно и которое затем улучшил немецкий математик Карл Вейерштрасс (1815—1897). Об этом рассказывается в главе 6. Так как мгновенная скорость, с которой движется тело, является производной, то трудности при делении ноля на ноль препятствовали развитию физики, пока Ньютон не решил эту проблему, создав анализ бесконечно малых. До конца XVII века, когда был сформирован анализ бесконечно малых, ученые могли изучать только простейшие виды движения: равномерное движение, при котором пройденный путь пропорционален затраченному времени, следовательно, скорость постоянна, а ускорение отсутствует, а также равноускоренное движение, при котором пройденный путь пропорционален квадрату времени, скорость пропорциональна времени, а ускорение постоянно. Для изучения последнего вида движения, примером которого является падение тела под действием силы тяжести, потребовался гений Галилея, который понял его суть за несколько десятков лет до того, как с помощью анализа бесконечно малых было найдено тривиальное решение этой задачи. Проиллюстрируем это на примере. Рассмотрим, как и в прошлых примерах, движущееся тело, которое в момент времени t прошло расстояние в s(t) = √t. Время будем измерять в секундах, расстояние — в метрах. Вычислить среднюю скорость движения тела несложно: например, в период времени с первой по четвертую секунду средняя скорость будет равна отношению пройденного пути и затраченного времени:средняя скорость = (s(4) – s(1))/(4-1) = (2 – 1)/3 = 1/3 м/с.
Но что, если нас интересует не средняя скорость, а мгновенная скорость в конкретный момент времени? Чтобы упростить рассуждения, допустим, что мы хотим вычислить мгновенную скорость в тот момент, когда проходит ровно одна секунда от начала движения. Выберем приращение времени h и вычислим среднюю скорость в интервале времени от 1 секунды до (1 + h) секунд: Чтобы вычислить мгновенную скорость в первую секунду, достаточно свести приращение времени h к нулю. Однако в этом случае снова возникает неопределенность:
Чтобы вычислить мгновенную скорость в первую секунду, достаточно свести приращение времени h к нулю. Однако в этом случае снова возникает неопределенность:
 Это происходит потому, что мгновенная скорость соответствует значению производной функции пройденного пути s(t) = √t. в момент времени t = 1.
В предыдущей таблице с числами указано, что значение этой производной должно равняться 0,5. Покажем, что это и в самом деле так, устранив неопределенность следующим способом:
Это происходит потому, что мгновенная скорость соответствует значению производной функции пройденного пути s(t) = √t. в момент времени t = 1.
В предыдущей таблице с числами указано, что значение этой производной должно равняться 0,5. Покажем, что это и в самом деле так, устранив неопределенность следующим способом:
 Умножим числитель и знаменатель на √(1+h) + 1 и упростим выражение:
Умножим числитель и знаменатель на √(1+h) + 1 и упростим выражение:
 Если в последнем выражении свести приращение времени h к нулю, то мы уже не столкнемся с неопределенностью и делением на ноль. Как и следовало ожидать, при h = 0 значение дроби будет равно 0,5. На языке физики это означает:
Если в последнем выражении свести приращение времени h к нулю, то мы уже не столкнемся с неопределенностью и делением на ноль. Как и следовало ожидать, при h = 0 значение дроби будет равно 0,5. На языке физики это означает:
мгновенная скорость в момент времени 1 = 1/2 = 0,5.
Следовательно, мы устранили изначальную неопределенность, которая возникает из-за деления ноля на ноль, и получили, что если тело проходит за t секунд √t метров, то по прошествии 1 секунды оно будет двигаться со скоростью 1/2 м/с.Интегралы
Другим базовым понятием анализа бесконечно малых является понятие интеграла. Интеграл используется для вычисления площади, ограниченной графиком функции. Например, пусть дана функция f, определенная на интервале между а и b. Значение интеграла будет равно площади следующей фигуры:
будет равно площади следующей фигуры:
 Символ ∫ для обозначения интеграла придумал Лейбниц (об этом подробно рассказывается в главе 4). Этот символ представляет собой стилизованную букву S — первую букву латинского слова summa («сумма»).
Интеграл применяется не только для вычисления площадей: в математике он также используется для расчета объемов, длин и определения центра тяжести. В физике ему соответствует понятие работы. Работа, которую необходимо совершить,. чтобы переместить тело под действием силы f из точки а в точку b, рассчитывается по формуле:
Символ ∫ для обозначения интеграла придумал Лейбниц (об этом подробно рассказывается в главе 4). Этот символ представляет собой стилизованную букву S — первую букву латинского слова summa («сумма»).
Интеграл применяется не только для вычисления площадей: в математике он также используется для расчета объемов, длин и определения центра тяжести. В физике ему соответствует понятие работы. Работа, которую необходимо совершить,. чтобы переместить тело под действием силы f из точки а в точку b, рассчитывается по формуле:
 Интеграл также используется для расчета пройденного телом пути, если известна скорость тела. Рассмотрим в качестве примера физическую задачу, о которой мы говорили в самом начале этой главы: какой путь пройдет тело спустя 4 секунды после начала движения, если в течение t секунд оно двигалось со скоростью, равной t2 м/с? Ответ вычисляется по следующей формуле:
Интеграл также используется для расчета пройденного телом пути, если известна скорость тела. Рассмотрим в качестве примера физическую задачу, о которой мы говорили в самом начале этой главы: какой путь пройдет тело спустя 4 секунды после начала движения, если в течение t секунд оно двигалось со скоростью, равной t2 м/с? Ответ вычисляется по следующей формуле:
 Задача сводится к вычислению этого интеграла. Если интерпретировать интеграл как площадь фигуры, он будет соответствовать площади, ограниченной участком параболы. Эту площадь вычислил Архимед еще 2300 лет назад. Это открытие наряду с другими принесло ему вечную славу: Архимеда по праву можно считать одним из величайших основателей интегрального исчисления (об этом более подробно рассказывается в главе 2).
Строгое определение интеграла, в котором не участвует понятие площади, — непростой вопрос с точки зрения логики. Здесь, пусть и в несколько иной форме, в дело снова вступают бесконечно малые величины. Из рисунка на предыдущей странице видно, что искомая фигура состоит из отрезков длиной f(t), где t принимает все возможные значения на интервале от а до b. Площадь искомой фигуры представляет собой сумму «площадей» этих отрезков. Однако эти отрезки имеют нулевую ширину, поэтому может показаться, что они не имеют площади. Мы вновь сталкиваемся с понятием бесконечно малой величины — ширины этих отрезков. В нотации, придуманной Лейбницем для обозначения интегралов, площадь фигуры, ограниченной кривой, понимается как сумма бесконечно малых: согласно рисунку на предыдущей странице, все отрезки, образующие фигуру, имеют высоту f(t).
Согласно Лейбницу, бесконечно малая ширина обозначается dt. Площадь этих «отрезков» равна произведению их основания на высоту, то есть f(t) dt, а площадь фигуры, которую мы хотим вычислить, равна сумме этих площадей: ∫f(t)dt.
Смысл этой суммы так и не смогли объяснить ни Ньютон, ни Лейбниц, создатели анализа бесконечно малых. По сути, первое точное определение интеграла было дано почти полтора столетия спустя усилиями Коши. В нем также используется понятие предела (более подробно об этом рассказывается в главе 6).
Вычисление площадей криволинейных поверхностей — очень сложная задача, в чем на собственном опыте убедились предшественники Ньютона и Лейбница. В некотором смысле эта задача аналогична задаче о вычислении интеграла. Вычисление интегралов во многих случаях (но не всегда) упрощает основная теорема анализа.
Задача сводится к вычислению этого интеграла. Если интерпретировать интеграл как площадь фигуры, он будет соответствовать площади, ограниченной участком параболы. Эту площадь вычислил Архимед еще 2300 лет назад. Это открытие наряду с другими принесло ему вечную славу: Архимеда по праву можно считать одним из величайших основателей интегрального исчисления (об этом более подробно рассказывается в главе 2).
Строгое определение интеграла, в котором не участвует понятие площади, — непростой вопрос с точки зрения логики. Здесь, пусть и в несколько иной форме, в дело снова вступают бесконечно малые величины. Из рисунка на предыдущей странице видно, что искомая фигура состоит из отрезков длиной f(t), где t принимает все возможные значения на интервале от а до b. Площадь искомой фигуры представляет собой сумму «площадей» этих отрезков. Однако эти отрезки имеют нулевую ширину, поэтому может показаться, что они не имеют площади. Мы вновь сталкиваемся с понятием бесконечно малой величины — ширины этих отрезков. В нотации, придуманной Лейбницем для обозначения интегралов, площадь фигуры, ограниченной кривой, понимается как сумма бесконечно малых: согласно рисунку на предыдущей странице, все отрезки, образующие фигуру, имеют высоту f(t).
Согласно Лейбницу, бесконечно малая ширина обозначается dt. Площадь этих «отрезков» равна произведению их основания на высоту, то есть f(t) dt, а площадь фигуры, которую мы хотим вычислить, равна сумме этих площадей: ∫f(t)dt.
Смысл этой суммы так и не смогли объяснить ни Ньютон, ни Лейбниц, создатели анализа бесконечно малых. По сути, первое точное определение интеграла было дано почти полтора столетия спустя усилиями Коши. В нем также используется понятие предела (более подробно об этом рассказывается в главе 6).
Вычисление площадей криволинейных поверхностей — очень сложная задача, в чем на собственном опыте убедились предшественники Ньютона и Лейбница. В некотором смысле эта задача аналогична задаче о вычислении интеграла. Вычисление интегралов во многих случаях (но не всегда) упрощает основная теорема анализа.
Основная теорема анализа
Анализ бесконечно малых — своеобразный мост между производными и интегралами: основная теорема анализа гласит, что интегрирование и вычисление производной являются взаимно обратными операциями. Точнее говоря, если мы хотим вычислить интеграл то, согласно основной теореме анализа, достаточно найти функцию F такую, что
то, согласно основной теореме анализа, достаточно найти функцию F такую, что
F’(t) = f(t)
для любого t в интервале между а и b. В этом случае Функция f должна обладать еще одним свойством — непрерывностью, на котором мы не будем останавливаться подробно.
Рассмотрим на примере, как основная теорема анализа упрощает вычисление интеграла
Функция f должна обладать еще одним свойством — непрерывностью, на котором мы не будем останавливаться подробно.
Рассмотрим на примере, как основная теорема анализа упрощает вычисление интеграла
 Этот интеграл в зависимости от его интерпретации можно использовать для расчета площади, ограниченной параболой; площади, ограниченной спиралью Архимеда; а также пути, пройденного телом, которое движется со скоростью v(t) = t2.
Согласно основной теореме анализа, достаточно найти функцию, производной которой будет функция t2. Это нетрудно сделать с помощью правила вычисления производной степенной функции:
Этот интеграл в зависимости от его интерпретации можно использовать для расчета площади, ограниченной параболой; площади, ограниченной спиралью Архимеда; а также пути, пройденного телом, которое движется со скоростью v(t) = t2.
Согласно основной теореме анализа, достаточно найти функцию, производной которой будет функция t2. Это нетрудно сделать с помощью правила вычисления производной степенной функции:
f(t) = tn.
Тогдаf’(t) = tn-1.
Отсюда нетрудно вывести, что производная функции t3/3 в точности равна t2. Следовательно: Как мы уже упоминали выше, путь, пройденный за 4 секунды телом, которое в течение t секунд движется со скоростью t2, определяется интегралом:
Как мы уже упоминали выше, путь, пройденный за 4 секунды телом, которое в течение t секунд движется со скоростью t2, определяется интегралом:
 Следовательно, достаточно подставить в предыдущую формулу а = 0 и b = 4:
Следовательно, достаточно подставить в предыдущую формулу а = 0 и b = 4:
 Рассмотрим спираль Архимеда — кривую, получаемую равномерным движением точки вдоль луча, который, в свою очередь, равномерно вращается вокруг своего начала. Будем считать, что точка движется вдоль луча со скоростью 1м/с, скорость вращения луча постоянна. Чтобы найти площадь, ограниченную первым витком спирали Архимеда, нужно вычислить интеграл
Рассмотрим спираль Архимеда — кривую, получаемую равномерным движением точки вдоль луча, который, в свою очередь, равномерно вращается вокруг своего начала. Будем считать, что точка движется вдоль луча со скоростью 1м/с, скорость вращения луча постоянна. Чтобы найти площадь, ограниченную первым витком спирали Архимеда, нужно вычислить интеграл
 Достаточно подставить в предыдущую формулу а = 0 и b = 2π
Достаточно подставить в предыдущую формулу а = 0 и b = 2π
 Именно этот результат получил сам Архимед, который изложил его иначе: «Площадь первого витка спирали равна трети площади круга, радиус которого равен длине пути, пройденного точкой вдоль прямой во время первого витка». В самом деле, так как на первом витке спирали точка проходит вдоль прямой путь, равный 2π, круг этого радиуса будет иметь площадь p ∙ (2π)2 = 4π3, о чем пишет Архимед.
Именно этот результат получил сам Архимед, который изложил его иначе: «Площадь первого витка спирали равна трети площади круга, радиус которого равен длине пути, пройденного точкой вдоль прямой во время первого витка». В самом деле, так как на первом витке спирали точка проходит вдоль прямой путь, равный 2π, круг этого радиуса будет иметь площадь p ∙ (2π)2 = 4π3, о чем пишет Архимед.
 Автор этой книги не ставил перед собой задачу подробно рассказать о понятиях и методах анализа бесконечно малых. Намного интереснее то, каким образом математики открыли эти понятия и как они изменялись со временем. В следующих главах мы расскажем об интеллектуальной эпопее длиной почти в две тысячи лет. Читатель узнает, как Ньютон, Лейбниц, Эйлер, Коши и другие великие математики создавали и последовательно видоизменяли понятия дифференциала, производной, интеграла и предела, пока они не приобрели тот вид, в котором известны нам сегодня.
Автор этой книги не ставил перед собой задачу подробно рассказать о понятиях и методах анализа бесконечно малых. Намного интереснее то, каким образом математики открыли эти понятия и как они изменялись со временем. В следующих главах мы расскажем об интеллектуальной эпопее длиной почти в две тысячи лет. Читатель узнает, как Ньютон, Лейбниц, Эйлер, Коши и другие великие математики создавали и последовательно видоизменяли понятия дифференциала, производной, интеграла и предела, пока они не приобрели тот вид, в котором известны нам сегодня.
Глава 2. От Архимеда до XVII века: истоки
В течение всего процесса формирования анализа бесконечно малых, длившегося почти две тысячи лет, со времен Архимеда до эпохи Ньютона и Лейбница, было создано множество различных математических теорий и концепций. Было вновь открыто и осмыслено наследие древних греков, в особенности работы Архимеда; появилась более сложная система счисления, чем древнегреческая и римская; и, разумеется, возникла алгебра и аналитическая геометрия, позволившая использовать методы алгебры при работе с кривыми. Стало возможным решать задачи о касательных, вычислении площади, центров тяжести, максимумов и минимумов и подобные им алгебраическим путем. Алгебра и аналитическая геометрия, по сути, стали тем языком, на котором можно было описать ранние этапы развития математического анализа. Это случилось благодаря усилиям плеяды ученых, которые совершили множество важных открытий, особенно в XVII веке. Этот процесс был очень сложным, интенсивным и интересным не только с научной, но и в большей степени с исторической точки зрения. На него влияли крупнейшие события в истории человечества, которые, в частности, привели к утрате классической греческой культуры и последующему возврату к ней, к научно -технической революции. Сказались на формировании этого раздела математики и проблемы обособленности, вызванные сложной политической ситуацией и многочисленными войнами в Европе в XVII веке. Не обошлось и без влияния интриг одних ученых против других, непримиримых споров, диспутов и оскорблений.Бесконечность в Древней Греции
Мы начнем наш рассказ с экскурса в Древнюю Грецию. Именно тогда математики и философы предприняли первые попытки понять бесконечность — метафизическую основу математического анализа. Для древних греков бесконечность была двухголовым монстром: с одной стороны — бесконечно малое, с другой — бесконечно большое. Бесконечность вскоре оказалась вовлечена в скандалы и споры. В некотором роде она проявилась в невозможности измерить одной мерой сторону квадрата и его диагональ, что разрушило пифагорейскую концепцию вселенной и привело к первому фундаментальному кризису в математике. Она также присутствовала в апориях Зенона о движении и множестве, в которых, помимо прочего, проявлялось диалектическое противоречие между различными философскими течениями той эпохи. Апории Зенона также показывают влияние этих противоречий на математику. Эти события привели к тому, что использование бесконечности было запрещено, точнее ограничено. Поскольку отрицать бесконечные процессы было невозможно («И в малом ведь нет наименьшего, но везде есть меньшее, — писал Анаксагор, — но и в отношении к большему всегда есть большее»), Аристотель попытался запретить использование актуальной бесконечности: «Бесконечное не может существовать как сущность или как свойство», — пишет он в книге 3 «Физики». Однако далее сам же признает: «Много невозможного получается, если вообще отрицать существование бесконечного, — это тоже очевидно», «О бытии можно говорить либо в возможности, либо в действительности, а бесконечное получается либо прибавлением, либо отнятием», иными словами, «величина не может быть бесконечной актуально, об этом уже сказано, но она может быть беспредельно делимой». Например, по Аристотелю, отрезок нельзя рассматривать как бесконечное множество точек, выстроенных в линию, однако допускается деление отрезка пополам неограниченное число раз. О роли бесконечности в математике Аристотель писал: «Наше рассуждение… не отнимает у математиков их исследования, ведь они теперь не нуждаются в таком бесконечном и не пользуются им; надо только, чтобы ограниченная линия была такой величины, как им [математикам] желательно». Хотя с точки зрения математики важнее другое его высказывание: «Всякую конечную величину [всегда] можно исчерпать любой определенной величиной». Это так называемая аксиома Архимеда о непрерывности. В действительности эту аксиому впервые сформулировал и использовал Евдокс, ученик Платона. Этот принцип позволил Евдоксу преодолеть кризис, возникший после того, как были открыты несоизмеримые величины. Аксиома Архимеда позднее упоминается в «Началах» Евклида в виде определения: «Говорят, что величины имеют отношение между собой, если они, взятые кратно, могут превзойти друг друга». На основе этой аксиомы Евдокс построил так называемый метод исчерпывания — строгий метод расчета площадей и объемов, который использовался, помимо прочего, для доказательства того, что площади кругов относятся как квадраты их диаметров. Это отношение мы называем числом π. Метод исчерпывания и, в частности, это утверждение позднее использовал Евклид в «Началах».Архимед
Однако настоящим мастером метода исчерпывания, вне всяких сомнений, был Архимед. В нескольких трудах он изложил свою аксиому о непрерывности: «Если имеются две неравные площади, то, постоянно прибавляя к самому себе избыток, на который большая площадь превосходит меньшую, можно получить площадь, которая была бы больше любой заданной ограниченной площади», — писал он в «Квадратуре параболы». Однако он признавал, что не был первооткрывателем этого метода: «Этой леммой пользовались и жившие ранее геометры», — писал он, имея в виду Евдокса. Архимед применял метод исчерпывания для решения многих задач. Мы уделим внимание одной из них, посвященной расчету площади спирали. Ученый рассматривал спираль, определение которой мы приводили в главе 1: эта спираль получается равномерным движением точки вдоль луча, который, в свою очередь, равномерно вращается вокруг своего начала. Архимед показал, что площадь первого витка спирали равна трети площади круга, радиус которого равен длине пути, пройденного точкой вдоль прямой во время первого витка. Чтобы доказать это, он построил фигуру несколько меньшей площади, состоявшую из п круговых секторов, полученных делением окружности на п равных частей, и другую фигуру большей площади, также состоявшую из n круговых секторов, в которую была вписана спираль, как показано на рисунке: Эти приближенные вычисления аналогичны тем, что используются сегодня при расчете площадей кривых в полярных координатах с помощью интегралов, и абсолютно эквивалентны разбиению площади под графиком кривой на прямоугольники при определении на заданном интервале определенного интеграла функции.
Именно по этой причине Архимед считается одним из авторов первых, примитивных аналогов интегрального исчисления.
Однако существует и другая причина, по которой Архимед удостоился этого почетного звания. К сожалению, эта причина никак не повлияла на математиков последующих эпох. Речь идет об утерянном трактате Архимеда «Метод».
Эвристические рассуждения Архимеда, приводимые в этой книге, также предшествовали созданию интегрального исчисления. Похожие идеи появились в математике лишь спустя две тысячи лет после Архимеда, в XVII веке. Идея Архимеда противоречила аристотелеву отрицанию актуальной бесконечности.
Его революционная гипотеза состояла в том, что площадь рассматривалась как совокупность отрезков, а объем — как совокупность площадей. Так, прямоугольник представлялся как совокупность отрезков, параллельных его стороне, а цилиндр — как совокупность кругов, параллельных его основанию. Эти совокупности обязательно должны были быть бесконечными — здесь и появляется актуальная бесконечность, которую отрицал Аристотель.
Эти приближенные вычисления аналогичны тем, что используются сегодня при расчете площадей кривых в полярных координатах с помощью интегралов, и абсолютно эквивалентны разбиению площади под графиком кривой на прямоугольники при определении на заданном интервале определенного интеграла функции.
Именно по этой причине Архимед считается одним из авторов первых, примитивных аналогов интегрального исчисления.
Однако существует и другая причина, по которой Архимед удостоился этого почетного звания. К сожалению, эта причина никак не повлияла на математиков последующих эпох. Речь идет об утерянном трактате Архимеда «Метод».
Эвристические рассуждения Архимеда, приводимые в этой книге, также предшествовали созданию интегрального исчисления. Похожие идеи появились в математике лишь спустя две тысячи лет после Архимеда, в XVII веке. Идея Архимеда противоречила аристотелеву отрицанию актуальной бесконечности.
Его революционная гипотеза состояла в том, что площадь рассматривалась как совокупность отрезков, а объем — как совокупность площадей. Так, прямоугольник представлялся как совокупность отрезков, параллельных его стороне, а цилиндр — как совокупность кругов, параллельных его основанию. Эти совокупности обязательно должны были быть бесконечными — здесь и появляется актуальная бесконечность, которую отрицал Аристотель.
ПАЛИМПСЕСТ АРХИМЕДА
В 1906 году датский эрудит Йохан Людвиг Гейберг обнаружил в Константинополе палимпсест — древнюю рукопись, где сохранились следы более ранней рукописи с трудами Архимеда. Поверх этого математического трактата был написан молитвенник для воскресных служб и других христианских праздников. Среди найденных работ была и ранее неизвестная — «Метод». Судя по особенностям почерка, рукопись относится примерно к 975 году н. э., а религиозные тексты, написанные поверх нее, датируются примерно 1229 годом.

ЗНАЧЕНИЕ БЕСКОНЕЧНОСТИ
Архимед также был первым греческим математиком, вычислившим сумму бесконечного числа слагаемых. Он рассматривал следующую сумму:

Ее требовалось рассчитать, чтобы определить площадь, ограниченную участком параболы. Несмотря на бесконечное число слагаемых (все они являются степенями 1/4), значение суммы конечно. Чтобы вычислить его, Архимед применил следующий прием: он умножил сумму на 1 - 1/4. Получим:

Теперь разделим результат на (1 - 1/4). Так как 1 - 1/4 = 3/4, при делении получим:
 Тот факт, что сумма бесконечного числа слагаемых равна конечному числу, доказывает, почему Ахиллес в действительности сможет догнать черепаху в знаменитой апории Зенона: сумма бесконечного числа временных интервалов, каждый из которых равен половине предыдущего, является конечной.
Тот факт, что сумма бесконечного числа слагаемых равна конечному числу, доказывает, почему Ахиллес в действительности сможет догнать черепаху в знаменитой апории Зенона: сумма бесконечного числа временных интервалов, каждый из которых равен половине предыдущего, является конечной.
* * *
Как мы уже говорили, эта идея снова появилась в математике лишь в XVII веке, в работах Бонавентуры Кавальери, Грегуара де Сен-Венсана и других, о чем мы расскажем позднее. Этим математикам были известны труды Архимеда, которые были напечатаны примерно в середине XVI века, но не «Метод», поэтому они были вынуждены заново открыть этот прием, сыгравший основную роль в появлении исчисления.
Согласно хроникам, Архимед погиб от рук солдата при захвате Сиракуз римлянами в 212 году до н. э. На иллюстрации — мозаика, найденная на раскопках Помпеи.
От Архимеда до XVII века
Лишь в XVII веке математики овладели приемами, описанными в трудах Архимеда, что ускорило появление анализа бесконечно малых. Следует упомянуть, что до того ученые Средневековья и эпохи Возрождения совершили несколько открытий, без которых было бы невозможно появление математического анализа. Однако важнейшие из них не связаны напрямую с исчислением, поэтому мы расскажем о них лишь вкратце. Речь идет в первую очередь о потере и повторном обретении и освоении наследия древних греков. Ключевую роль также сыграло распространение по всей Европе индийской системы счисления. Этот длительный и непростой процесс начался в X веке, а позднее, в XIII—XVI веках, на севере Италии возникли школы абака — образовательные центры для тех, кто занимался торговлей. В конце XVI века десятичная система счисления также начала применяться для записи рациональных и иррациональных чисел. Решающую роль в ее распространении наряду с Франсуа Виетом (1540—1603) сыграл Симон Стевин (1548—1620), хотя использованная им нотация была не совсем удобной. Стевин, уроженец бельгийского города Брюгге, развил свою идею по причинам практического характера: «Десятичная система счисления есть класс арифметики, в основе которого лежит идея о прогрессии с основанием 10, где используются арабские цифры так, что в этой системе может быть записано любое число; и любая операция, с которой мы имеем дело в торговле, может быть выполнена с помощью только целых чисел, без использования дробей». Он предложил унифицировать единицы мер и весов, а также денежные единицы с применением новой системы счисления, но эта идея была воплощена в жизнь лишь после Великой французской революции. Некоторое время спустя идее Стевина последовали другие авторы, которые использовали современную нотацию с точкой (или запятой) для отделения десятичной части от целой. Среди них был шотландский барон Джон Непер (1550—1617), один из создателей логарифмов. Логарифмы появились в начале XVII века и были тесно связаны с открытием анализа бесконечно малых. Независимо от Непера логарифмы придумал и швейцарец Иост Бюрги (1552—1632). Изначально они использовались как вспомогательные функции в числовых расчетах, чтобы упростить умножение больших чисел в астрономических вычислениях. Нетрудно представить, сколько времени нужно было потратить на умножение множества подобных чисел и сколь велик был риск ошибиться. Джон Непер писал: «Ничто не причиняет столько проблем при занятиях математикой и не делает вычисления столь неприятными и затруднительными, как умножение, деление и извлечение квадратных и кубических корней из больших чисел. Операции эти помимо потери времени в большинстве случаев являются источником ошибок». Чтобы упростить умножение больших чисел, в то время использовался метод под названием простаферезис. В его основе лежала тригонометрическая формула, с помощью которой произведение преобразовывалось в сумму. По сути, Джон Непер создал логарифмы с целью упростить этот метод: ему были нужны таблицы, с помощью которых можно было бы напрямую преобразовывать произведения в суммы. Метод простаферезиса заключается в следующем. Допустим, мы хотим перемножить два больших числа n и m. Пусть они состоят из восьми цифр каждое — стандартная ситуация для астрономических расчетов тех времен. Для этого найдем в таблице значений косинусов два числа а и b такие, что n = cos a, m = cos b. Затем с помощью таблицы определим значения cos (a — b) и cos (a + b), после чего применим следующую формулу: Если бы мы выполняли умножение напрямую, нам нужно было бы последовательно восемь раз умножить первое число на каждую цифру второго, после чего сложить восемь полученных чисел из восьми или девяти цифр каждое. С помощью вышеприведенной формулы и тригонометрических таблиц мы свели умножение к трем операциям сложения и простому делению на 2.
Метод простаферезиса был в некотором роде техническим инструментом: он позволял сэкономить время при расчетах, и его можно считать примитивным алгоритмом для вычислительной машины. Поэтому в течение определенного времени он держался в секрете и был доступен лишь немногим избранным. Непер, например, узнал об этом методе не самым обычным способом. Эта история больше напоминает сюжет приключенческого романа. Джон Крэйг, врач шотландского короля и друг Непера, в конце XVI века совершил путешествие в Данию, чтобы подобрать королю невесту. Корабль попал в шторм, и ему пришлось причалить к побережью вблизи лучшей обсерватории того времени, которую Тихо Браге построил на острове Вен между Данией и Швецией. Путешественников приютили в обсерватории, и, пока бушевал шторм, Крэйг познакомился с методом простаферезиса, а по возвращении в Шотландию обучил ему Джона Непера.
До XVII века было совершено крайне мало открытий, напрямую связанных с анализом бесконечно малых. Можно упомянуть о французском философе Николае Орезмском (ок. 1323—1382). Он дал примитивное определение понятия функции и ее графического представления: «Всё, что изменяется — реально ли измерить его или нет — можно вообразить как непрерывную величину, представленную отрезком». Он также внес вклад в изучение бесконечных рядов, впервые доказав, что сумма
Если бы мы выполняли умножение напрямую, нам нужно было бы последовательно восемь раз умножить первое число на каждую цифру второго, после чего сложить восемь полученных чисел из восьми или девяти цифр каждое. С помощью вышеприведенной формулы и тригонометрических таблиц мы свели умножение к трем операциям сложения и простому делению на 2.
Метод простаферезиса был в некотором роде техническим инструментом: он позволял сэкономить время при расчетах, и его можно считать примитивным алгоритмом для вычислительной машины. Поэтому в течение определенного времени он держался в секрете и был доступен лишь немногим избранным. Непер, например, узнал об этом методе не самым обычным способом. Эта история больше напоминает сюжет приключенческого романа. Джон Крэйг, врач шотландского короля и друг Непера, в конце XVI века совершил путешествие в Данию, чтобы подобрать королю невесту. Корабль попал в шторм, и ему пришлось причалить к побережью вблизи лучшей обсерватории того времени, которую Тихо Браге построил на острове Вен между Данией и Швецией. Путешественников приютили в обсерватории, и, пока бушевал шторм, Крэйг познакомился с методом простаферезиса, а по возвращении в Шотландию обучил ему Джона Непера.
До XVII века было совершено крайне мало открытий, напрямую связанных с анализом бесконечно малых. Можно упомянуть о французском философе Николае Орезмском (ок. 1323—1382). Он дал примитивное определение понятия функции и ее графического представления: «Всё, что изменяется — реально ли измерить его или нет — можно вообразить как непрерывную величину, представленную отрезком». Он также внес вклад в изучение бесконечных рядов, впервые доказав, что сумма
1 + 1/2 + 1/3 + 1/4 + 1/5 + …
равна бесконечности.ДОКАЗАТЕЛЬСТВО НИКОЛАЯ ОРЕЗМСКОГО
По словам самого Николая Орезмского, причина, по которой сумма гармонического ряда
1 + 1/2 + 1/3 + 1/4 + 1/5 + …
равна бесконечности, такова: «К величине, равной 1, прибавим 1/2, 1/3, 1/4 и следующие дроби, сумма которых равна бесконечности. В самом деле из членов этого ряда можно составить бесконечное число групп, сумма которых будет больше 1/2. Так, 1/3 + 1/4 больше 1/2, так как каждое из двух слагаемых больше 1/4. Аналогично,
1/5 + 1/6 + 1/7 + 1/8
больше 1/2, так как каждое из четырех слагаемых больше 1/8. Аналогично
1/9 + 1/10 + … + 1/16
больше 1/2, так как каждое из восьми слагаемых больше 1/16, и так до бесконечности».
Наука в Европе XVII века
Перед тем как рассказать об открытиях, совершенных в XVII веке, в результате которых появился анализ бесконечно малых, будет уместно описать ситуацию в европейской науке начала XVII века. Во-первых, нужно уточнить, что математика и наука в целом тогда не были уделом профессионалов, как в наше время. В университетах не проводились научные исследования, а полученные результаты обычно не изучались более подробно — можно сказать, что это было не принято. Почти никто из ученых, о которых мы расскажем на следующих страницах, не был профессиональным математиком: некоторые были юристами, другие — архитекторами, дипломатами, богословами, и лишь очень немногие зарабатывали на жизнь математикой или же были как-то связаны с университетами. Поэтому когда мы называем кого-либо математиком, это означает, что этот ученый внес вклад в развитие математики, но мог иметь совершенно иную сферу профессиональных и научных интересов. Это привело к ряду неудобств. Исследователи объединялись вокруг одного ученого или любителя науки, подобные группы часто были изолированными друг от друга или враждовали, что было вызвано вопросами патриотизма или спорами о научных состязаниях или турнирах, которые в ту эпоху проводились очень часто. По всем этим причинамполученные результаты распространялись неэффективно: как правило, о них упоминали в письмах друзьям или знакомым, далее, спустя некоторое время (иногда крайне длительное) эти знания оформлялись в виде книг, которые также не становились достоянием широкого круга. В этих условиях лучшее математическое образование давали не университеты, а отдельные ученые. Одним из ведущих научных обществ первой половины XVII века была Accademia Nazionale dei Lincei (Национальная академия деи Линчей), в которой состоял Галилей. Академия была основана в Риме в 1603 году и прекратила свое существование спустя 30 лет. Центром, возможно, важнейшего научного общества был монах францисканского ордена минимов Марен Мерсенн (1588—1648). Мерсенн, который жил в Париже начиная с 1610-х годов, создал кружок математиков и ученых, встречи которого проводились еженедельно. Мерсенн помогал многим европейским ученым и философам поддерживать переписку с Дезаргом, Ферма и Паскалем (последний начал посещать встречи кружка в конце 1630-х, будучи еще подростком). Кружок также способствовал распространению философских трудов Декарта и астрономических трактатов Галилея. Помимо организаторской работы, Мерсенн также внес вклад в математику и акустику. В начале XVII века было восстановлено практически все математическое и научное наследие Древней Греции, сохранившееся после бурных времен Средневековья. Хотя «Начала» Евклида и другие базовые труды были хорошо известны и изучены, более глубокие и сложные трактаты, в частности книги Архимеда, были поняты лишь несколько десятилетий спустя. Их освоение сыграло решающую роль в создании анализа бесконечно малых. Некоторые из отцов-основателей исчисления, в частности Валлис и Барроу, имели в личной библиотеке экземпляры трудов Архимеда. Достаточно сказать, что Архимед был наиболее цитируемым автором во всех книгах о вычислении площадей и объемов, написанных в течение всего этого столетия. Однако один из аспектов математики Архимеда и древнегреческой математики вообще радикально изменился. Речь идет о логической строгости изложения. Математика XVII века была намного менее строгой и четкой, чем древнегреческая. Может показаться, что это был шаг назад, однако именно эта смена парадигмы в итоге позволила преодолеть границы, обозначенные в древнегреческой математике, и, в частности, создать математический анализ. В отличие от ученых Древней Греции, математиков XVII века интересовали открытия, а не безупречно строгие доказательства. Чем была вызвана эта смена парадигмы? Этому можно привести различные объяснения, в том числе и философские: ученые XVII века не находились под влиянием философии Платона, которой и была обусловлена строгость логического изложения, свойственная греческой математике. Причины этому могут носить исторический характер: XVI и XVII века были временем самых разнообразных открытий: географических (открытие Америки в конце XV века стало результатом не точных логических рассуждений, а, напротив, ошибки Колумба при вычислении радиуса Земли), астрономических (гелиоцентрическая теория Коперника), медицинских (кровообращение) и технических (изобретение книгопечатания Гуттенбергом, создание микроскопа и телескопа). Математики предпочитали уделять основное внимание разработке новых методов, с помощью которых можно было совершать открытия, не заботясь о логической строгости этих методов. В рамках такого подхода бесконечность использовалась без аристотелевских ограничений, и бесконечно малые и бесконечно большие величины стали применяться очень широко. Изначально они применялись для вычисления площадей, объемов, углов наклона касательных, центров тяжести, максимумов, минимумов и так далее. Решением этих задач занималась целая плеяда математиков начала XVII века, так называемые предшественники математического анализа. Позднее бесконечно малые позволили Ньютону и Лейбницу создать две похожие версии анализа бесконечно малых. Наконец, уже в XVIII веке Эйлер, несомненно, великий знаток бесконечного, создал математический анализ, в котором функции изучались с помощью методов анализа бесконечно малых. Если говорить об обстоятельствах, способствовавших созданию исчисления, следует упомянуть еще об одном крупном направлении в математике XVII века — аналитической геометрии.БЕСКОНЕЧНОСТЬ КАК НЕЧТО БОЖЕСТВЕННОЕ
Существует еще одна причина, которую можно назвать теологической, благодаря которой в XVII веке бесконечность стала использоваться более свободно, чем в Древней Греции. Это связано с восприятием бесконечности как атрибута всемогущего христианского Бога. Следуя заветам Аристотеля, богословы отказывали человеку в возможности понять актуальную бесконечность, но им не оставалось другого выбора, кроме как перевести это понятие в область богословия. Так, Фома Аквинский рассматривал Бога как полную и всеобъемлющую актуальную бесконечность. Такая трактовка достаточно часто встречается в трудах философов XVII века. Подтверждение этому мы находим у Декарта: «Мыслю некоего вышнего Бога — вечного, бесконечного, всеведущего, всемогущего, творца всех сущих, помимо него самого, вещей», а также: «Что же до Бога, я считаю его столь бесконечным, что к его совершенству ничего уже нельзя добавить»; у Спинозы: «Под Богом я разумею существо абсолютно бесконечное (ens absolute infinitum), то есть субстанцию, состоящую из бесконечно многих атрибутов, из которых каждый выражает вечную и бесконечную сущность», а также у Лейбница: «Следует считать, что эта божественная субстанция, неделимая, универсальная и непреложная, не должна иметь пределов и содержать всю реальность, какую только возможно». Некоторые из этих философов также были учеными и математиками. Лейбниц, например, был одним из создателей математического анализа. Ньютон, еще один из отцов-основателей анализа, также был богословом и верил во всемогущего Бога.
Аналитическая геометрия позволила сопоставить кривым уравнения. Например, окружности единичного радиуса, то есть кривой, все точки которой отстоят на одну единицу от фиксированной точки, называемой центром, соответствует уравнение x2 + y2 = 1. Также стало возможным сопоставить уравнениям кривые, в результате чего математики смогли изучить намного больше кривых. Теперь, чтобы задать новую кривую, вместо определения ее геометрических свойств требовалось лишь написать соответствующее уравнение. Кроме того, стало возможным применение алгебраических методов для решения геометрических задач, в частности задач на вычисление площадей, определение углов наклона касательных и так далее. На смену частным геометрическим методам пришли более общие — алгебраические. Например, расчет угла наклона касательной для разных кривых радикально отличался, а методы алгебры, в частности нахождение производной, позволяли определять угол наклона касательной одним и тем же способом для всех кривых. Для этого достаточно было использовать алгоритм, созданный на основе правил вычисления производной. Следует осознать всю важность открытия этих общих правил, скрытых за неимоверным числом частных результатов, которые были накоплены за первые три четверти XVII века, Именно общие правила аналитической геометрии позволили Ньютону и Лейбницу стать первооткрывателями математического анализа.
Вычисление квадратуры и кубатуры
Вернемся в начало XVII века и расскажем подробнее о методах анализа бесконечно малых, ставших основой математического анализа. Начнем с методов вычисления площадей и объемов, или, говоря языком той эпохи, расчета квадратур и кубатур. Из всех методов, появившихся в первой трети этого столетия для решения подобных задач, наиболее важным был метод неделимых, предложенный учеником Галилея, преподавателем Болонского университета Бонавентурой Кавальери (1598— 1647). В одном ряду с ним стоят только методы вычисления объема, разработанные Кеплером, которые использовались австрийскими виноделами при изготовлении бочек. Можно сказать, что в основе метода неделимых лежали принципы, предложенные еще Архимедом. Кавальери рассматривал площади фигур как множество линий, объемы — как множество плоских сечений. Множество линий, образующих плоскую фигуру, Кавальери называл omnes linae («все линии»). Стало возможным сравнение площадей любых двух плоских фигур путем сравнения соответствующих им omnes linae: согласно Кавальери, «фигуры относятся друг к другу, как все их линии, взятые по любой регуле», как показано на иллюстрации. Метод Кавальери был применим не только для расчета площадей, но также для расчета объемов тел. Он попытался разработать целую теорию неделимых, которая позволила бы доказать полученные им результаты без использования понятия бесконечности (как строили свои доказательства древнегреческие математики). Однако в его рассуждениях очевидно используется актуальная бесконечность. Это стало определенным преимуществом, так как именно явное присутствие бесконечности привело к тому, что метод Кавальери оказался более гибким, пусть и менее строгим, чем метод исчерпывания, к которому прибегали греки. С помощью своего метода неделимых Кавальери вычислил площадь фигур, ограниченных параболой общего вида xn для n = 3, 4, 5, 6 и 9. Тем самым он намного опередил Архимеда, который провел расчеты площади лишь для параболы и спирали, которым соответствовала функция х2.
По сравнению с открытыми позднее способами вычисления площадей и объемов метод неделимых Кавальери обладает рядом недостатков: он недостаточно общий, слишком зависит от геометрических рассуждений, не говоря уже о логической небезупречности. Однако этот метод позволил найти новые квадратуры и кубатуры и превзойти результаты, полученные древнегреческими математиками.
Кроме того, недостатки этого метода вскоре удалось преодолеть. Так, Эванджелиста Торричелли (1608—1647), друг Кавальери, мастерски использовал этот метод и нашел различные строгие доказательства в стиле древнегреческих математиков, а Ферма, Паскаль и Валлис, а также Роберваль (1602—1675) и его метод бесконечно малых преобразовали геометрический метод Кавальери в алгебраический, благодаря чему он стал более общим и его стало возможно применять более широко.
Метод Кавальери был применим не только для расчета площадей, но также для расчета объемов тел. Он попытался разработать целую теорию неделимых, которая позволила бы доказать полученные им результаты без использования понятия бесконечности (как строили свои доказательства древнегреческие математики). Однако в его рассуждениях очевидно используется актуальная бесконечность. Это стало определенным преимуществом, так как именно явное присутствие бесконечности привело к тому, что метод Кавальери оказался более гибким, пусть и менее строгим, чем метод исчерпывания, к которому прибегали греки. С помощью своего метода неделимых Кавальери вычислил площадь фигур, ограниченных параболой общего вида xn для n = 3, 4, 5, 6 и 9. Тем самым он намного опередил Архимеда, который провел расчеты площади лишь для параболы и спирали, которым соответствовала функция х2.
По сравнению с открытыми позднее способами вычисления площадей и объемов метод неделимых Кавальери обладает рядом недостатков: он недостаточно общий, слишком зависит от геометрических рассуждений, не говоря уже о логической небезупречности. Однако этот метод позволил найти новые квадратуры и кубатуры и превзойти результаты, полученные древнегреческими математиками.
Кроме того, недостатки этого метода вскоре удалось преодолеть. Так, Эванджелиста Торричелли (1608—1647), друг Кавальери, мастерски использовал этот метод и нашел различные строгие доказательства в стиле древнегреческих математиков, а Ферма, Паскаль и Валлис, а также Роберваль (1602—1675) и его метод бесконечно малых преобразовали геометрический метод Кавальери в алгебраический, благодаря чему он стал более общим и его стало возможно применять более широко.

Фрагмент мраморной статуи Бонавентуры Кавальери, хранящейся в Академии искусств Милана. Ученый изображен размышляющим над бесконечно малыми величинами.
Перед рассказом о том, как Валлис усовершенствовал метод Кавальери, остановимся на личности Грегуара де Сен-Венсана (1584—1667), иезуита, ученика Христофора Клавия и придворного учителя короля Испании Филиппа IV. По поручению папы Григория XIII Сен-Венсан разработал новый календарь и поощрял занятия математикой среди иезуитов. Он совершил значимые открытия во многих областях. Так, он расширил геометрический метод интегрирования, который позднее оказал влияние на работы Паскаля. Однако эта работа была опубликована с заметным опозданием — лишь в 1647 году, хотя была завершена в конце 1620-х годов. К тому времени Сен-Венсан стал уделять больше внимания алгебраическим методам, разработанным под влиянием аналитической геометрии. Он также был автором работы о геометрических рядах, которую Гюйгенс рекомендовал к изучению Лейбницу. Результаты, полученные в этой работе, Сен-Венсан использовал в обсуждении знаменитой апории Зенона об Ахиллесе и черепахе. Он указывал, что Зенон не учел, что отрезки, которые нужно пройти Ахиллесу, образуют геометрическую прогрессию со знаменателем 1/2 и, несмотря на то что эта прогрессия имеет бесконечное множество членов, ее сумма является конечной. Однако наиболее значимым вкладом Сен-Венсана, на наш взгляд, является обнаружение связи между логарифмами и площадью фигуры, ограниченной гиперболой. Выражаясь языком той эпохи, он доказал, что если длина интервалов возрастает геометрически, то площадь фигуры увеличивается арифметически, что показано на иллюстрации. Теперь пришло время рассказать о Джоне Валлисе (1616—1703), одном из основателей Лондонского королевского общества и главе кафедры геометрии в Оксфорде с 1649 года. Возможно, этот пост был пожалован ему за то, что он расшифровал перехваченные сообщения роялистов во время Гражданской войны в Англии. В библиотеке Валлиса были двуязычные издания трудов греческих авторов (на латинском и греческом языках), в том числе Архимеда. Валлис также был автором грамматики английского языка (1653).
Он видоизменил метод неделимых Кавальери, присвоив им числовые значения. Таким образом, на смену геометрическим преобразованиям при вычислении площадей фигур пришли арифметические расчеты. Кроме того, Валлис ввел примитивную операцию, подобную переходу к пределу. Валлис достаточно свободно использовал бесконечные процессы (стоит напомнить, что именно он является автором знака бесконечности ∞, который мы используем и поныне), сделав тем самым еще один шаг от безупречной логической строгости к открытию новых, более мощных методов. Степень этих изменений можно увидеть, если обратить внимание на названия трудов Кавальери и Валлиса: труд Кавальери носил название Geometria indivisibilibus continuorum nova quadam ratione promota, книга Валлиса — Arithmetica infinitorum. Труд Валлиса отличается общим характером арифметических и алгебраических расчетов по сравнению с частными геометрическими доказательствами Кавальери; он также полностью использует широкие возможности бесконечности, в то время как Кавальери вынужден формулировать строгие и логичные доказательства в древнегреческом стиле, что, безусловно, накладывало свои ограничения. Показательным для того времени является следующий комментарий Валлиса относительно недостаточной логической строгости его метода: «Этот метод является в высшей степени еретическим, однако его можно подтвердить с помощью хорошо всем известного метода вписанных и описанных фигур, что излишне, поскольку частые повторения отвлекают читателя. Любой сведущий в этом предмете может выполнить такое доказательство». Это один из немногих случаев, когда в книге фигурирует термин «доказательство». Будучи под впечатлением от созданного им арифметического метода, с помощью неполной индукции и интуиции Валлис смог рассчитать площадь всех парабол вида xr, где r — любое рациональное число, не равное —1. Более того, ему удалось найти удивительную формулу для расчета числа π:
Теперь пришло время рассказать о Джоне Валлисе (1616—1703), одном из основателей Лондонского королевского общества и главе кафедры геометрии в Оксфорде с 1649 года. Возможно, этот пост был пожалован ему за то, что он расшифровал перехваченные сообщения роялистов во время Гражданской войны в Англии. В библиотеке Валлиса были двуязычные издания трудов греческих авторов (на латинском и греческом языках), в том числе Архимеда. Валлис также был автором грамматики английского языка (1653).
Он видоизменил метод неделимых Кавальери, присвоив им числовые значения. Таким образом, на смену геометрическим преобразованиям при вычислении площадей фигур пришли арифметические расчеты. Кроме того, Валлис ввел примитивную операцию, подобную переходу к пределу. Валлис достаточно свободно использовал бесконечные процессы (стоит напомнить, что именно он является автором знака бесконечности ∞, который мы используем и поныне), сделав тем самым еще один шаг от безупречной логической строгости к открытию новых, более мощных методов. Степень этих изменений можно увидеть, если обратить внимание на названия трудов Кавальери и Валлиса: труд Кавальери носил название Geometria indivisibilibus continuorum nova quadam ratione promota, книга Валлиса — Arithmetica infinitorum. Труд Валлиса отличается общим характером арифметических и алгебраических расчетов по сравнению с частными геометрическими доказательствами Кавальери; он также полностью использует широкие возможности бесконечности, в то время как Кавальери вынужден формулировать строгие и логичные доказательства в древнегреческом стиле, что, безусловно, накладывало свои ограничения. Показательным для того времени является следующий комментарий Валлиса относительно недостаточной логической строгости его метода: «Этот метод является в высшей степени еретическим, однако его можно подтвердить с помощью хорошо всем известного метода вписанных и описанных фигур, что излишне, поскольку частые повторения отвлекают читателя. Любой сведущий в этом предмете может выполнить такое доказательство». Это один из немногих случаев, когда в книге фигурирует термин «доказательство». Будучи под впечатлением от созданного им арифметического метода, с помощью неполной индукции и интуиции Валлис смог рассчитать площадь всех парабол вида xr, где r — любое рациональное число, не равное —1. Более того, ему удалось найти удивительную формулу для расчета числа π:
 Арифметические методы Валлиса для вычисления площадей оказали огромное влияние на Ньютона, который подтвердил, что идеи о биноме и других основных понятиях математического анализа возникли у него после тщательного изучения книги Валлиса во время учебы в Кембридже. Сам Валлис предложил любопытную родословную анализа бесконечно малых.
1. Метод исчерпывания (Архимед).
2. Метод неделимых (Кавальери).
3. Арифметика бесконечного (Валлис).
4. Метод бесконечных рядов (Ньютон).
Арифметические методы Валлиса для вычисления площадей оказали огромное влияние на Ньютона, который подтвердил, что идеи о биноме и других основных понятиях математического анализа возникли у него после тщательного изучения книги Валлиса во время учебы в Кембридже. Сам Валлис предложил любопытную родословную анализа бесконечно малых.
1. Метод исчерпывания (Архимед).
2. Метод неделимых (Кавальери).
3. Арифметика бесконечного (Валлис).
4. Метод бесконечных рядов (Ньютон).
Центры тяжести
С расчетом площади и объема тесно связана задача об определении центра тяжести. В конце XVI века, после того как был обнаружен труд Архимеда «О равновесии плоских фигур», некоторые математики начали уделять внимание решению подобных задач. Среди них были два переводчика трудов Архимеда на латынь Франческо Мавролико (1494—1575) и Федерико Коммандино (1509—1575), а также Симон Стевин, который систематизировал и упростил методы Архимеда. Несколько позднее появились работы швейцарского математика Пауля Гюльдена (1577—1643), который повторно открыл теорему об объемах тел вращения и центрах тяжести, известную как теорема Гюльдена, хотя она упоминается еще в «Собрании» Паппа Александрийского: «Объем тела вращения равен площади фигуры, умноженной на длину окружности, радиусом которой служит расстояние от оси вращения до центра тяжести фигуры». Гюльден вел ожесточенный спор с Кавальери (оба они были иезуитами) о методе неделимых: швейцарец обвинял Кавальери, с одной стороны, в плагиате кеплеровских идей, с другой — в отсутствии логической последовательности при рассмотрении площади как совокупности отрезков. Гюльдену удалось привести простое и элегантное геометрическое построение, где метод неделимых Кавальери вел к противоречию. Однако доказательство Гюльдена, которое он привел для своей теоремы, изобиловало метафизическими рассуждениями и было еще более спорным, чем методы Кавальери. Последний не замедлил указать на это в ответ на нападки Гюльдена.Расчет угла наклона касательной
Методы анализа бесконечно малых, связанные с расчетами угла наклона касательной, наряду с задачами вычисления объемов и площадей относятся к числу задач, изучение которых привело к появлению математического анализа. Само понятие касательной, «прямой, которая касается кривой в одной точке», вызвало множество трудностей, так как с помощью аналитической геометрии Ферма и Декарта можно было с легкостью вводить новые кривые, и, как следствие, предметом изучения математиков стал широкий спектр различных кривых. В этом смысле интересный пример представляют логарифмы, появившиеся как средство упрощения операций умножения, деления и извлечения корня из больших чисел, что использовалось в астрономических наблюдениях. Это позволило составить очень точные таблицы положений звезд и небесных тел. В итоге была введена логарифмическая функция и соответствующая ей кривая, для которой можно вычислить ограниченную ею площадь, угол наклона касательной и так далее. Рост числа изучаемых кривых привел к тому, что старое определение касательной как прямой, которая касается кривой в одной точке, стало не вполне удобным. Кроме того, потребовались новые методы нахождения касательных к новым кривым. Следует упомянуть метод, предложенный Ферма, также применимый в задачах определения максимумов и минимумов и для спрямления кривых. В знак признания этих и других работ о квадратурах некоторые французские математики XVII века (французом был и Ферма) считали его создателем математического анализа. Важность этих результатов Ферма несколько преувеличена, но сам Ньютон в письме, найденном в 1934 году, признавал, что в своих работах по математическому анализу он опирался на метод касательных Ферма: «Указание я получил из метода касательных Ферма. Применив его к абстрактным уравнениям прямым и обратным способом, я придал этому методу общий характер». Как бы то ни было, Ферма, «король среди любителей», как называл его шотландский математик и писатель Эрик Темпл Белл, имея в виду его непрофессиональные занятия математикой, занимает почетное место в истории науки. Это право он заслужил не только за предполагаемое доказательство своей знаменитой теоремы, для которого оказались «слишком узки» поля книги. Другие математики, помимо Ферма, также разработали новые методы для определения углов наклона касательных, но практически во всех использовались бесконечно малые величины. Так, можно упомянуть Роберваля и его кинематический метод для нахождения касательной к спирали, который также использовали Галилей, Торричелли и Архимед. Заслуживает упоминания Декарт и его метод, представленный в труде «Геометрия», а также Барроу, Худде, де Слюза и их псевдодифференциальные методы. Все они обладали схожими недостатками: они были в достаточной степени применимы к алгебраическим кривым, но требовали изменений для каждой конкретной кривой, что было чрезвычайно сложно, а иногда и вовсе невозможно сделать для трансцендентных кривых. Все эти методы были унифицированы с помощью дифференциала, введенного Лейбницем, и флюксии, введенной Ньютоном. Эти понятия были близки к современной производной. В середине этого же столетия возник важный класс задач, имевший большое историческое значение, в которых требовалось определить кривую по известным свойствам ее касательной. Первую задачу такого типа сформулировал юрист и ученик Декарта Флоримон де Бон (1601—1652). Возможно, самой известной из предложенных им задач является задача о нахождении кривой с постоянной подкасательной. Эту задачу не удалось решить самому Декарту, и вся слава досталась Лейбницу: как вы увидите чуть позже, он привел решение в первой в истории книге по анализу бесконечно малых и тем самым продемонстрировал всю мощь созданного им метода. Для создания математического анализа обязательно (и неизбежно) требовалось признать, что задачи о касательной и о квадратуре являются обратными друг другу. Говоря современным языком, необходимо было показать, что дифференцирование и интегрирование — взаимно обратные операции. Именно в этом заключается основная теорема анализа, которая неспроста носит это название. Этот факт был известен Ферма, Торричелли и прежде всего Барроу, однако по причинам, о которых мы расскажем позднее, они не поняли всю его важность для решения задач, его значимость как связующего элемента двух классов задач — о касательных и квадратурах. Основная теорема анализа указала математикам путь, которым нужно следовать: выделять общее и наиболее значимое из множества частных случаев.
Исаак Барроу был учителем Ньютона. Его работы лежат в основе анализа бесконечно малых.
Исаак Барроу (1630—1677) был одним их тех гигантов, о которых говорил Ньютон в письме Роберту Гуку в феврале 1676 года: «Если я видел дальше других, то потому, что стоял на плечах гигантов» (из главы 3 вы узнаете, что эта фраза допускает еще одно, достаточно нелицеприятное толкование). Барроу был учителем Ньютона в Кембридже и первым лукасовским профессором математики. Он оставил этот пост в 1669 году (его заменил Ньютон), занялся богословием (он был англиканским пастором с 1660 года) и стал духовником короля Англии Карла II. Возможно, он подошел ближе всех к открытию математического анализа, за исключением Ньютона и Лейбница. Ему не хватало самой малости — знаний аналитической геометрии. Барроу создал метод нахождения касательных, очень похожий на вычисление производной. Кроме того, он добился важных результатов при решении задач по расчету площадей, а также доказал, что задачи нахождения касательной и задачи на вычисление площади являются обратными. Возможно, он руководствовался идеями Торричелли, с которым познакомился во время путешествия во Францию, Италию, Германию, Голландию и Константинополь, когда ему пришлось по религиозным мотивам покинуть Англию, где в то время правил Оливер Кромвель. Его доказательство приводится в лекции X его книги Lectiones geometricae. Оно является чисто геометрическим и выполняется для монотонных кривых. В нем также используется старое определение касательной как прямой, которая касается кривой в единственной точке. Чего же не хватило Барроу, чтобы открыть анализ бесконечно малых? Ему требовалось перейти от частной задачи нахождения касательной к общей задаче определения изменения функции, то есть ввести понятие, эквивалентное понятию флюксии у Ньютона или, с небольшими отличиями, понятию дифференциала у Лейбница, а также разработать алгоритм расчетов (правила нахождения производной). Однако для этого Барроу требовалась аналитическая геометрия: она позволила бы описать кривые (геометрические объекты) с помощью формул (алгебраических объектов) и перейти от задачи нахождения касательной к задаче определения производной функции. Алгебраические методы были также обязательными для создания правил вычисления производных. С другой стороны, без сведения процесса нахождения кривой (вычисления производной) к простому алгоритмическому методу с возможностью инвертирования (то, что мы называем вычислением первообразной) тот факт, что задачи нахождения касательной и определения квадратуры являются взаимно обратными, был бы не слишком полезен. По этой причине Барроу не осознал всю значимость доказанного им утверждения. Барроу не нравилась алгебраизация геометрии, выполненная Ферма и Декартом, что в итоге стоило ему авторства математического анализа. Он оставил этот почетный титул Лейбницу и Ньютону. Математический анализ появился во время научной революции, продолжавшейся весь XVII век, и решающую роль в этом сыграли два ученых первой величины: Исаак Ньютон и Готфрид Лейбниц. О математическом анализе можно говорить тогда, когда обобщены два базовых понятия (прообразы современной производной и интеграла), разработаны алгоритмы их вычисления (правила вычисления производной) и показано, что эти понятия являются взаимно обратными (это утверждение сегодня известно как основная теорема анализа). Для решения задач нахождения касательной, максимумов и минимумов, квадратуры, центра тяжести и других, которыми занимались предшественники Лейбница и Ньютона, достаточно использовать эти базовые понятия, должным образом интерпретированные, и применять алгоритм их вычисления, основанный на правилах, о которых мы рассказали в главе 1.Глава 3. Ньютон, последний из волшебников
День 13 июля 1936 года стал поворотным в изучении биографии Исаака Ньютона и его наследия. В этот и последующий день на аукционе «Сотбис» было продано 332 лота: рукописи, письма и другие документы, принадлежавшие Ньютону. Запутанная история рукописей Ньютона не лишена очарования, так как она открывает перед нами истинный портрет ученого, более сложный и многогранный, чем было принято считать в XVIII и XIX веках. Сохранилось огромное количество рукописей, писем и других документов Ньютона, несмотря на то что, по его собственным словам, в последние месяцы жизни он сжег большую часть писем, а также некоторые статьи невысокого качества, которые не хотел передавать потомкам. Возможно, это и в самом деле было так, но стоит отметить, что Ньютон окружил себя ореолом тайн и загадок, что сделало его практически легендарной фигурой. Взять хотя бы удивительную и всем известную историю с яблоком, принесшую ему славу гения. Сам Ньютон рассказал эту историю Уильяму Стьюкли незадолго до своей смерти. Это одна из четырех дошедших до нас версий; источником их всех является сам Ньютон, которому на тот момент было уже за семьдесят. Вот что пишет Стьюкли: «После обеда установилась теплая погода, мы вышли в сад и пили чай в тени яблонь. Он [Ньютон] сказал мне, что мысль о гравитации пришла ему в голову, когда он точно так же сидел под деревом. Он находился в созерцательном настроении, когда неожиданно с ветки упало яблоко. “Почему яблоки всегда падают перпендикулярно земле? — подумал он. — Почему не в сторону и не вверх, а всегда к центру земли?” Очевидно, причина состоит в том, что земля притягивает его. Вещество должно обладать силой притяжения, и центр притяжения к Земле должен находиться в центре Земли, а не где-либо еще. Поэтому яблоко падает перпендикулярно земле в направлении ее центра. <…> Существует сила, которую мы будем именовать гравитацией, простирающаяся на всю Вселенную», Однако вернемся к истории с рукописями. После смерти Ньютона, который не оставил завещания, произошла размолвка между восемью возможными наследниками — потомками двоих дочерей и сына матери Ньютона от второго брака с протестантским священником Барнабой Смитом. За исключением любимой племянницы Ньютона Кэтрин Бартон и ее супруга Джона Кондуита, остальные наследники хотели без промедлений получить доход от наследства, поэтому в июле 1727 года, вскоре после смерти ученого, его библиотека была продана некоему Джону Хаггинсу за 300 фунтов — на 30 фунтов больше изначально объявленной стоимости. Также были проданы все бумаги Ньютона, которые были готовы к публикации.
Иллюстрация к истории о яблоке, после которой, как говорят, у Ньютона и родилась идея о теории всемирного тяготения.
Документы и рукописи Ньютона, которые не удалось продать, перешли к дочери супругов Кондуит, которую также звали Кэтрин. В 1740 году она вышла замуж за виконта Лаймингтона. Далее бумаги перешли к их сыну, который стал графом Портсмутским — отсюда и название «Портсмутская коллекция», под которым часто упоминают наследие Ньютона. В 1872 году было начато составление первой описи бумаг Ньютона, для чего они были переданы в Кембриджский университет. Результаты описи были опубликованы в 1888 году, после чего все документы вернулись в семью графа Портсмутского, за исключением статей по математике, писем, книг и других документов, которые были подарены университету семьей графа. Остальные бумаги, как мы уже упоминали, были проданы на аукционе «Сотбис» в 1936 году. К ним относились все рукописи об алхимии, химии и по вопросам, связанным с британской казной; все материалы, собранные Джоном Кондуитом для будущей биографии Ньютона; объемная переписка, юношеские дневники, рукописи о хронологии, богословии и об анализе бесконечно малых, два удивительной красоты портрета и посмертная маска. Всё это было продано в течение двух дней за сумму, слегка превышавшую 9000 фунтов. Нетрудно представить, каково было разочарование нового графа Портсмутского, который выставил наследство на продажу, так как остро нуждался в деньгах. Экономист Джон Мейнард Кейнс приобрел личные документы и рукописи по алхимии, хронологии, истории и богословию, после чего передал их Королевскому колледжу Кембриджа. Большая часть рукописей по богословию была приобретена востоковедом Абрахамом Яхудой (он выменял некоторые документы у Кейнса), который завещал их Национальной библиотеке Израиля в Иерусалиме, куда они поступили в 1966 году, после того как были улажены все спорные вопросы с наследством.Великий мыслитель
Интенсивнейшие работы по изучению трудов и личности Ньютона, проведенные во время Второй мировой войны, с которыми не сравнятся никакие исследования, посвященные другим ученым, можно считать своеобразной аллегорией этого аукциона, на котором было выставлено бесценное и практически нетронутое наследие сэра Исаака Ньютона. В результате представление о Ньютоне как ученом и человеке изменилось. Знаменитая фраза Джона Мейнарда Кейнса, произнесенная в ходе изучения коллекции рукописей, приобретенной им на аукционе «Сотбис», отлично это иллюстрирует: «Ньютон не был первым в эпохе рационализма. Он был последним из волшебников, последним из вавилонян и шумеров, последним великим умом, который взирал на мир так же, как и те, что 10 000 лет назад начали формировать наше интеллектуальное наследие». Ньютона представляли как ученого с большой буквы, отца современной физики, первооткрывателя закона всемирного тяготения, автора глубоких исследований о природе света и цветов, автора анализа бесконечно малых, великого мыслителя, причем в создание этого образа внес вклад и сам ученый. Однако в его рукописях перед нами предстает более сложный и вместе с тем более реальный портрет человека, который интересовался не только наукой, но и проблемами богословия, проводил эксперименты в области алхимии, а также, помимо «Математических начал натуральной философии» и «Оптики», написал непростые для понимания труды по библейской хронологии. Их и при его жизни сложно было отнести к научным, однако они более объемны, чем научные работы Ньютона. Его карьера казалась безупречной. Будучи сравнительно молодым, он стал лукасовским профессором математики в Кембридже, затем — членом британского парламента, управлял Монетным двором и Лондонским королевским обществом. Однако рукописи, проданные на аукционе, раскрывают постыдный секрет: по религиозным взглядам Ньютон был близок к еретическому арианству. Если бы это стало известно, он немедленно лишился бы всех своих постов. Помимо статей о наиболее подходящих сплавах для чеканки монет, рукописи содержат диатрибы, направленные против Святой Троицы, полные ужасных и сюрреалистичных эпизодов, близких к жестокому реализму и даже порнографии. Цитата из одной из многочисленных рукописей Ньютона по богословию (в ней идет речь о пророчествах) дает общее представление об этом: «И поскольку Римская церковь стала править над десятью царями и прельстила их этой идолопоклоннической религией, обретя за счет этого богатство и власть, она сравнима с женщиной, облаченной в пурпурные и алые ткани и увешанной драгоценностями, которая восседает подобно королеве на семи холмах, распутничает с земными царями и опьяняет народы своим распутством, наводняет их золотом, серебром и драгоценными камнями, и жемчугом, и полотнами тонкой работы, и шелками, и другими драгоценностями и обогащает земных купцов своею роскошью». Не лишен иронии тот факт, что Ньютон, ярый противник Святой Троицы, был членом Тринити-колледжа (Колледжа Святой Троицы) в течение всего периода, проведенного в Кембридже.
Шотландский скульптор Эдуардо Паолоцци, вдохновленный знаменитым портретом Уильяма Блейка, создал этот скульптурный образ Ньютона, воздвигнутый в 1995 году возле Британской библиотеки в Лондоне.
Трудное детство гения
Первое из череды событий, определивших непростой характер Ньютона, произошло за три месяца до его рождения, в Рождество 1642 года по юлианскому календарю, который в то время использовался в Англии. Этим событием стала смерть его отца. Согласно Фрэнку Мэнюэлю, автору интересного психологического исследования о Ньютоне, опубликованного в 1968 году, с течением времени место отца заняла фигура Бога Отца. Так, всю свою жизнь Ньютон искал истину с помощью науки, богословия и алхимии, а его собеседником были не современники, а отец, фигуру которого в представлении Ньютона заменил сам Бог Отец. Это объясняет, почему Ньютон был столь непримирим по отношению к малейшей критике своих научных трудов. В результате у него развился абсурдный страх публикации открытий, из-за чего его труды по математике были изданы со значительным опозданием. Некоторые работы, посвященные главным образом анализу бесконечно малых, были опубликованы спустя 40 и даже 50 лет после того, как были написаны, а некоторые не были изданы вовсе. Всё это приводило к спорам, кто же первый открыл математический анализ: Лейбниц, который не боялся публиковать результаты своих трудов, или Ньютон.
Чертеж телескопа Ньютона, который хранится в Лондонском королевском обществе. Включен в сборник его писем. На заднем плане расположена статуя ученого.
Эти споры разгорелись после выхода в свет его первой научной работы в 1672 году. В январе того года Ньютон был избран членом Лондонского королевского общества после того, как представил созданный им телескоп-рефлектор. В следующем месяце он опубликовал свою первую работу в журнале Королевского общества «Философские записки», в которой изложил новую теорию света и цвета. Эта публикация вселила большие надежды в ученые круги Англии и всей Европы. Тут же появились неизбежные критики и несогласные с работой Ньютона. Однако это не были какие-то безвестные ученые: новую теорию света не принял Роберт Гук, считавшийся ведущим авторитетом в области оптики, и Христиан Гюйгенс, лидер европейской науки. Ричард Вестфолл, автор лучшей биографии Ньютона, вышедшей в 1980 году, так объясняет результаты публикации: «Полемика, последовавшая за публикацией, больше говорит о самом Ньютоне, чем об оптике. В течение восьми лет он вел грандиозную борьбу за правду. Гениальность Ньютона требовала свою цену. Восемь лет бессонных ночей, восемь лет непрерывного напряжения, в течение которых он искал Истину там, куда никогда раньше не ступал человеческий разум. Страх того, что глупцы отвлекут его внимание от новых сражений, которые он вел в других областях, стала последней каплей. В 1672 году Ньютон уже работал над своей теорией в течение шести лет, и она казалась ему очевидной. Однако все остальные считали, что эта теория противоречит здравому смыслу, и отказывались принять ее. Они не признавали силу и убедительность его доказательств, и Ньютон быстро потерял интерес к дискуссии. Он был готов лишь к моментальному и всеобщему принятию его теории. Необходимость защищать и объяснять то, что для него было очевидно, и спровоцировала кризис». В психологической интерпретации событий, предлагаемой Ф. Мэнюэлем, задача Ньютона как исследователя, тот самый поиск Истины, о котором упоминает Вестфолл, превращается в религиозную проблему. Его собеседником был Бог, отождествляемый с отцом: «Неточность в тексте рукописи, провал эксперимента или несерьезность его интерпретации не просто шли вразрез с научным методом, но были греховными, подобно лжи во время исповеди. Ложь на исповеди была тягчайшим преступлением, так как тем самым ставился под сомнение акт Божьего творения». И еще: «Ошибка в научном методе уподоблялась греху, так как была результатом лени и недостаточно усердного служения Богу. Для Ньютона грех был не проявлением человеческой слабости, о котором можно забыть, но знаком того, что грешник находится под властью зла».
Гравюра начала XIX века, на которой изображен отчий дом Ньютона в Вулсторпе близ Грэнтема в английском графстве Линкольншир.
В возрасте трех лет Ньютон пережил большую травму, одну из самых серьезных в его жизни: его мать, Анна Эйскоу, вышла замуж за священника Барнабу Смита, которому было 63 года, и прекратила отношения с сыном. Супруги поселились в доме Смита в нескольких километрах от дома Ньютонов, где маленький Исаак остался жить под опекой бабушки со стороны матери. Отделение от матери было болезненным и сильно повлияло на личность Ньютона: он стал с величайшим подозрением относиться ко всему, что можно было расценить как попытку лишить его чего бы то ни было. Это объясняет ожесточенные споры о первенстве, которые он вел с разными учеными, в особенности с Лейбницем, на протяжении всей жизни. Мэнюэль так описывает последствия разлуки с матерью: «Мать Ньютона занимает центральное место в его жизни. <…> Они были вместе в течение важнейшего периода в его жизни, и его фиксация по отношению к ней была абсолютной. Травма, вызванная ее уходом, отрицание его любви породили в нем тоску, агрессивность и страх. После безграничного обладания, в которое не вмешивался никто, даже отец (как если бы речь шла о непорочном зачатии), мать отказалась от него и бросила. Некоторые психологи указывают, что волнения, вызванные разлукой с родителями, выражаются острее всего, если родители покидают ребенка в возрасте от 13 до 18 месяцев, другие указывают более ранний период в жизни ребенка. Так как Ньютону на момент второго брака матери было уже 36 месяцев, этот наиболее опасный период должен был завершиться. Однако близость нового материнского дома могла еще больше усилить боль от потери. Элегантная колокольня церкви Северного Уитхэма возвышалась над прочими постройками и виднелась на несколько миль вокруг. Анна жила там со священником Смитом — едва ли в полутора милях от дома, где жил ее сын. Ньютон так никогда и не оправился от травмы, которую нанесла ему потеря матери по вине другого мужчины. Поэтому всякий раз, когда кто-либо пытался отнять у него то, что он считал своим, его обуревала ярость и одновременно грусть, вызванная этой первой и столь тяжелой потерей. Он считал, что совершил все свои открытия и получил все титулы самостоятельно, и малейшая угроза потерять их вызывала в нем мучительное беспокойство». Его мать вновь овдовела в 1653 году и вернулась в старый дом. Вместе с ней вернулись трое детей от второго брака, который продлился семь лет. Наследство отчима составило несколько сотен книг, преимущественно по богословию. Они, несомненно, пробудили интерес Ньютона к богословию, который сохранялся в течение всей жизни. В одной из записных книжек Ньютона найдено его признание в грехах, совершенных до 1662 года, когда ему было 20 лет. Двадцать третий и двадцать четвертый пункт в перечне грехов звучат так: «…угрожал моему отцу и матери Смит, что сожгу их в доме»; «…желал смерти и ожидал этого». Весьма вероятно, что когда в 1715 году Ньютон писал, имея в виду Лейбница и его анализ бесконечно малых: «…у того, кто совершил открытие вторым, нет прав на него», призрак преподобного Смита, второго мужа его матери, наверняка стоял перед его глазами. Ньютон был принят в школу Грэнтема в восьми километрах от дома, когда ему было 12, и провел там несколько лет. В Грэнтеме он жил в доме аптекаря, в приемную дочь которого он мог быть влюблен (она поняла это, когда ей было уже 82 года!). Если неловкие ухаживания юноши, не привыкшего общаться с девочками, можно назвать романом, то это был первый и последний роман в жизни Ньютона. Юный Ньютон поступил в Кембридж в начале лета 1661 года, преодолев сопротивление матери с помощью ее брата, который учился именно там. Ньютон жил и работал в Кембридже 35 лет. За это время он совершил все свои научные открытия, хотя, возможно, большую часть времени он посвящал другим занятиям: богословию, библейской истории и главным образом алхимии. Вне всяких сомнений, он был гением. Мало того, в течение всей жизни Ньютон отличался невероятной трудоспособностью, особенно ярко проявившейся в кембриджский период. Он работал практически беспрерывно, забывая о сне и еде, закрывшись в комнате, посвятив себя занятиям оптикой, физикой и математикой. Его вклад в эти научные дисциплины поистине огромен. Однако большую часть времени, судя по невероятному числу рукописей на эти темы, он бесстрашно пытался понять свои эксперименты в области алхимии, искал доказательства, которые укрепили бы его веру, непрестанно находился в поисках истины или, что более применимо в его случае, вел бесконечный диалог с Богом Отцом. Огромные усилия и работа без передышки — явное указание на это содержится в названии книги Вестфолла «Неугомонный» (Never at rest) — четко отражены в его рукописях: «Из его рукописей видно, что он совершал ошибки и учился на них, порой следовал неверным путем и не всегда сразу понимал противоречивость своих идей. Рукописи однозначно дают понять: его открытия не были результатом озарений или вспышек гениальности».На службе науки. «Начала»
Попробуем продемонстрировать разницу между предполагаемыми озарениями, когда открытие совершалось вмгновение ока — именно таково упрощенное представление о труде гения, которым многие считают Ньютона, — и долгой и сложной работой. Работой, состоящей в том, чтобы увидеть первые ростки идеи, очистить ее, выделить суть, согласовать с другими идеями, объяснить ее, часто с помощью уже совершенных открытий и исследований. Именно так на самом деле работал Ньютон. Расскажем о том, как Ньютон совершил одно из своих крупнейших открытий — закон всемирного тяготения, и написал свою важнейшую работу — «Математические начала натуральной философии». И вновь напомним, что Ньютон всегда, а особенно в последние годы жизни, был скорее не гением-провидцем, а неутомимым тружеником. Об этом свидетельствует уже упомянутая история с яблоком или еще одно его высказывание о том, как он совершал свои открытия: «Я всегда держал задачу у себя на виду, пока из первых проблесков она не превращалась в яркий свет». В других случаях он был более реалистичен. Так, в письме, датированном 10 декабря 1692 года, он писал, что «Начала» были написаны только благодаря «трудолюбию и длительным размышлениям». В начале 1680-х годов Гук объединился со знаменитым архитектором и преподавателем астрономии в Оксфорде Кристофером Реном, а также с юным астрономом Эдмундом Галлеем, чтобы найти ответ на вопрос, логичным образом возникший в теории центральных сил Гука: по какой орбите будет двигаться планета, на которую действует центральная сила притяжения, обратно пропорциональная квадрату расстояния? Галлей лучше других понял, как найти решение: он обратился с вопросом к Ньютону. Встреча состоялась в августе 1684 года. Содержание беседы нам известно по рассказу Ньютона Абрахаму де Муавру, английскому математику, который родился во Франции, но покинул родину из-за религиозных притеснений. Последний впоследствии так рассказывал о встрече: «Доктор Галлей спросил его, какая кривая может описывать движение планет, если предположить, что сила их притяжения к Солнцу обратно пропорциональна квадрату расстояния до него. Сэр Исаак немедленно ответил, что орбиты планет будут иметь форму эллипса. Доктор выказал величайшую радость и, удивленный, спросил его, откуда ему это известно. «Потому что я это вычислил», — ответил Ньютон, после чего доктор Галлей попросил его незамедлительно показать эти расчеты. Сэр Исаак не смог найти их среди своих бумаг и пообещал выполнить расчеты повторно и отправить доктору Галлею».БЫЛ ЛИ ИЗВЕСТЕН ЗАКОН ТЯГОТЕНИЯ ДО НЬЮТОНА?
До того как на сцену вышел Ньютон, положение дел в изучении движения планет в Англии было следующим. Ведущим специалистом считался Роберт Гук, который позднее стал одним из величайших врагов Ньютона, Гук, взяв за основу принцип прямолинейной инерции, сформулированный Декартом, заменил центробежную силу и силу тяготения единственным принципом притяжения, который, по его мнению, и был причиной изменения исходной прямолинейной траектории. В 1670 году он изложил свои идеи на конференции, прошедшей в Лондонском королевском обществе, секретарем которого он являлся с 1677 по 1703 год. Его теория вкратце заключалась в следующем. 1. Все небесные тела обладают силой тяготения, или притяжения к центру, и притягивают все остальные небесные тела, которые находятся в радиусе действия этой силы. 2. Тела движутся по прямым линиям и только под действием силы меняют траекторию: окружность, эллипс или любую иную, более сложную. 3. Действие сил притяжения уменьшается по мере увеличения расстояния между телами по определенному закону. Закон этот на тот момент был неизвестен. Несколько лет спустя, проведя аналогию между тяготением и светом, Гук установил, что сила притяжения обратно пропорциональна квадрату расстояния.
Вернемся немного назад, к самому знаменательному периоду (anni mirabiles) в жизни Ньютона, который длился примерно двадцать месяцев, с 1665 по 1666 год. Этот период Ньютон провел в отчем доме в Вулсторпе, так как Кембриджский университет был закрыт из-за эпидемии чумы. Именно в это время Ньютон начал работу над теорией тяготения, и именно тогда произошла известная история с яблоком. В тот период Ньютон занимался решением задачи о движении планет в рамках теории вихрей Декарта — он изучил ее самостоятельно еще до поступления в Кембридж. Как и Гюйгенс, он использовал в качестве отправной точки закон прямолинейной инерции и считал, что изменение прямолинейной траектории обусловлено действием двух сил: силы тяготения и центробежной силы. Использовав наряду с этими гипотезами третий закон Кеплера, он обнаружил, что центробежные силы, действующие на планеты, изменяются обратно пропорционально квадрату их расстояния от Солнца. Несомненно, уже тогда он предполагал, что падение яблока на землю и вращение Луны вокруг Земли подчиняются одной и той же силе тяготения. Однако чтобы пройти путь от этой гипотезы до открытия закона всемирного тяготения, потребовался долгий и упорный труд. Изначально Ньютон пытался сравнить ускорение, вызванное центробежной силой, под действием которой движется Луна, с ускорением, вызванным силой тяготения у поверхности Земли. Его гипотеза была верной, но Ньютон отказался от нее, так как она не подтверждалась расчетами: он использовал неточное значение радиуса Земли. Кроме того, в то время он еще не знал, что следует измерять расстояние между центрами тел. Ньютон вернулся к задаче о движении планет лишь 10 лет спустя. Возможно, на него повлияло письмо Гука, полученное в 1676 году, в котором тот просил высказать мнение о гипотезе, согласно которой движение планет является следствием закона прямолинейной инерции и вызвано силой притяжения, направленной к центру орбиты. Эта сила, которую Ньютон позднее назвал центростремительной, пришла на смену силе тяготения и центробежной силе. Гипотеза Гука заставила Ньютона вновь обратиться к задаче о движении планет и впоследствии стала причиной серьезной вражды между Гуком и Ньютоном. Гук обвинил последнего в плагиате, когда тот заканчивал работу над «Началами». Ньютон обнаружил следующее: из двух первых законов Кеплера следует, что силы притяжения обратно пропорциональны квадрату расстояния. Именно об этих расчетах он упомянул во время встречи с Галлеем.

Слева — британская марка, выпущенная по случаю 300-летней годовщины издания «Начал».
На марке изображены планеты, движущиеся по эллипсам. Вверху — марка Никарагуа, на которой Солнечная система изображена внутри яблока рядом с формулой закона всемирного тяготения.
Расскажем, как развивались события, последовавшие за этой знаменательной встречей. Ньютон пересмотрел и дополнил свои вычисления и в ноябре 1684 года отправил Галлею небольшую статью на девяти страницах под названием De motu corporum in gyrum. В ней он привел наброски доказательства того, что траектория движения планеты под действием силы притяжения, обратно пропорциональной квадрату расстояния, является коническим сечением, а при скоростях, меньших определенного значения, траектория планеты принимает форму эллипса. В статье также содержался и обратный результат: как мы уже говорили, Ньютон получил его, взяв за основу гипотезу, изложенную в письме Гука. Благодаря настойчивости Галлея, гениальности и невероятной трудоспособности Ньютона через два с половиной года свет увидела книга De motu en los Philosophiae naturalis principia mathematica — «Математические начала натуральной философии». Члены Лондонского королевского общества, ознакомившись с рукописью, постановили: «Математические начала натуральной философии» господина Ньютона должны быть незамедлительно опубликованы форматом в четверть листа». Публикацию книги Галлею пришлось оплатить из своего кармана, что стало серьезным испытанием для юного члена Королевского общества. «Начала» были изданы в трех томах с предисловием, в котором, помимо прочего, изложены три закона Ньютона. В третьем томе под названием «Система мира» описываются законы движения небесных тел. В нем центростремительная сила, которая удерживает планеты на эллиптических орбитах, отождествляется с силой тяготения. Как следствие, сила, удерживающая Луну на орбите, — это та же самая сила, под действием которой предметы падают на поверхность Земли. Кроме того, сила тяготения действует на все тела во Вселенной. Она пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними. Так как следствием этого закона являются законы Кеплера о движении планет, это означает, что под действием этой же силы движутся спутники планет и кометы вокруг Солнца. Этим же объясняется неравномерность движения планет, которую Ньютон изучал на примере Луны. В предисловии к первому изданию «Начал» Галлей писал: «Мы наконец узнали, почему нам кажется, что Луна порой движется неравномерно, как будто насмехаясь над нами, когда мы пытаемся описать числами ее движение, до сей поры загадочное для любого астронома».
Обложка первого издания “Математических начал натуральной философии» с поправками, внесенными самим Ньютоном.
В «Системе мира» также рассматривались и другие вопросы. Заслуживает упоминания теория, по которой приливы вызваны притяжением Солнца и Луны, а также теория о форме планет, которые всегда сплющены у полюсов (форма планет определяет период их обращения вокруг своей оси). Последняя теория была окончательно подтверждена французскими экспедициями XVIII века в Лапландию и Перу, целью которых было измерение дуги меридиана. Эти экспедиции ознаменовали окончательный триумф системы Ньютона над системой Декарта.Ньютон и анализ бесконечно малых
Исаак Ньютон — один из самых известных и уважаемых ученых всех времен. Хотя это часто не принимается во внимание, но он в наибольшей степени обязан этой славе своим способностям к математике. Именно благодаря им он заметно выделялся среди других ученых того времени, и без них было бы невозможно написание его главного труда — «Математические начала натуральной философии». Иными словами, Ньютон открыл «систему мира», благодаря чему, как удачно заметил Лагранж, стал самым удачливым из всех ученых, поскольку существует лишь одна система мира, которую можно открыть. Именно благодаря глубоким знаниям математики, которыми не обладали его современники, Ньютон смог подкрепить и обосновать свои открытия. По словам Вестфолла, «математика была первой и главной страстью Ньютона. Именно из математики он заимствовал критерии логической строгости, которых неизменно придерживался на протяжении всего своего пути в науке. Ньютон собирался совершить плавание по неизвестным океанам мысли, из которых не вернулись многие искатели приключений XVII века. Ньютон не просто вернулся из этого путешествия — он привез с собой трофеи. Возможно, именно математическая дисциплина помогла ему добиться успеха». Многие считают, что Ньютон был исключительно физиком, точнее натурфилософом, или занимался прикладной математикой. Стоит напомнить, что писал по этому поводу Дерек Том Уайтсайд, составитель прекрасного восьмитомника рукописей Ньютона по математике: «Никогда не следует забывать, что математика была для Ньютона не просто набором инструментов для поиска истины. Она обладала внутренней красотой и силой, не зависящей от внешних причин и способов практического применения. Тем, кто не чувствует элегантность и мощь математики как самостоятельной дисциплины, я представляю Ньютона — «чистого» математика, который, как в библейской метафоре, удалился от мира в башню из слоновой кости в Кембридже, где занимался поисками новых теорем, свойств, алгоритмов и доказательств, элегантных самих по себе. И сколь удивительно он использовал свой талант и способности! В то время в мире не было более одаренного и разностороннего математика, никого, кто больше него разбирался бы в алгебре, геометрии и в тонкостях анализа бесконечно малых». Из всех математических открытий Ньютона, вне всяких сомнений, открытие анализа бесконечно малых было наиболее важно и имело наиболее значимые последствия. Первые идеи о математическом анализе появились у Ньютона в наиболее знаменательный период его жизни — в 1665—1666 годы. В рукописи, написанной им за несколько лет до смерти в 1727 году, мы читаем: «В начале 1665 года я открыл метод приближенного вычисления с помощью рядов, а также правило, по которому можно свести бином любой степени к такому ряду. В мае того же года я открыл метод построения касательных Грегори и де Слюза, а в ноябре получил метод флюксий. В январе следующего года я развил теорию цветов, в мае начал работать над обратным методом флюксий. В том же году я начал размышлять о тяготении применительно к орбите Луны и на основе законов Кеплера определил силы, которые удерживают планеты на орбитах». Его первая работа по математическому анализу «Анализ с помощью уравнений с бесконечным числом членов» (De analysi per aequationes numero terminorum infinitas) была завершена в 1669 году, но опубликована только в 1711-м. Эту книгу Ньютон написал в конце июня 1669 года (точные даты неизвестны) всего за несколько дней, взяв за основу результаты собственных исследований, проведенных в 1664 году. Ньютон использовал разложение логарифмической функции в степенной ряд, описанное Николасом Меркатором в книге Logarithmotechnia. Он также руководствовался слухами и предположениями о том, какими исследованиями в то время занимались другие ученые.
Первая страница английского издания «Анализа».
«Анализ с помощью уравнений с бесконечным числом членов» имел огромную ценность. После публикации этой работы, несмотря на ее небольшой объем, Ньютон был признан создателем анализа бесконечно малых, а его труд — основополагающим в этом новом разделе математики. В первой части книги Ньютон показывает, как с помощью степенного ряда можно произвести расчет квадратуры для множества функций, используя в качестве основы базовую квадратуруaxm/n
Рассуждения Ньютона стоит изложить подробнее. Для простоты мы приведем частный случай, описанный самим Ньютоном, для площади, ограниченной кривой, которая задается следующей формулой: Ньютон действовал так.
Ньютон действовал так.
 Увеличим на бесконечно малую величину, которую обозначим за о (это обозначение использовал сам Ньютон) абсциссу х. Площадь увеличится на площадь прямоугольника с вершинами x, y(x), y(x + o) и x + o, как показано на иллюстрации. Возьмем прямоугольник со сторонами o и v такой, что его площадь будет равна упомянутому приращению площади. Получим:
Увеличим на бесконечно малую величину, которую обозначим за о (это обозначение использовал сам Ньютон) абсциссу х. Площадь увеличится на площадь прямоугольника с вершинами x, y(x), y(x + o) и x + o, как показано на иллюстрации. Возьмем прямоугольник со сторонами o и v такой, что его площадь будет равна упомянутому приращению площади. Получим:
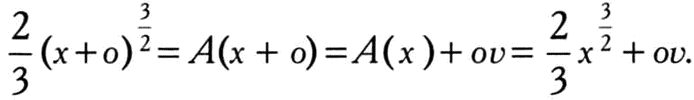 Возведя обе части в квадрат и упростив равенство, получим:
Возведя обе части в квадрат и упростив равенство, получим:
 Разделив обе части на о, получим:
Разделив обе части на о, получим:
 Если теперь мы примем прирост х бесконечно малым, то есть приравняем o к нулю, то v = y, и предыдущая формула примет вид
Если теперь мы примем прирост х бесконечно малым, то есть приравняем o к нулю, то v = y, и предыдущая формула примет вид
 Отсюда следует, что площадь, ограниченная кривой у = х2, равна 2/3 ∙ 3/2 x. Может показаться, что Ньютон пытался вычислить площадь, ограниченную кривыми определенного типа, но в действительности полученный им результат намного важнее. В первой части «Анализа» Ньютон хотел изложить общий алгоритм и подчеркнуть, что он применим не только в задачах расчета площади, «Все задачи о длине кривых, о величинах и о поверхностях тел и о центрах тяжести могут быть сведены в конце концов к определению плоской поверхности, ограниченной кривой», — делает он крайне важное замечание, за которым следует раздел под названием «Приложение вышеизложенного к другим примерам того же рода». Это замечание отделяет первую часть работы, в которой изложен общий метод, от второй, в которой излагаются различные способы его применения. Можно сказать, что результат его работы несколько неопределен: Ньютон видел огромную ценность найденного им абстрактного метода, однако, возможно, на начальном этапе, когда идея еще не оформилась окончательно, ему было сложно выразить ее доступно. Скорее всего, на этом этапе ему попросту не хватало терминов и обозначений. Он сосредоточил основное внимание на абстрактной задаче определения функции по известной производной. Кроме того, он рассматривает и обратную задачу о вычислении изменения функции (об этом рассказывается в конце книги). Наконец, он приводит краткий алгоритм расчета этого изменения (производной). Четкие правила вычисления производной позднее опубликовал Лейбниц, но не будем забывать, что в «Анализе» Ньютон изложил не все результаты, полученные им в области математического анализа к 1669 году.
Всё вышеизложенное позволяет заявить, что выход «Анализа» ознаменовал появление анализа бесконечно малых. «Анализ с помощью уравнений с бесконечным числом членов» — великолепный пример, позволяющий оценить акт творения в математике во всем его великолепии: при прочтении книги Ньютона мы становимся свидетелями процесса возникновения анализа бесконечно малых. Так, если мы углубимся в чтение «Анализа» и попытаемся увидеть уже известные нам термины и понятия современного математического анализа, это можно будет сравнить с просмотром детских фотографий человека, с которым мы познакомились уже в зрелом возрасте: сквозь еще не оформившиеся, детские черты уже проступает облик знакомого нам взрослого человека.
Закончив рукопись «Анализа», который принес автору известность среди британских математиков, Ньютон показал свой труд Барроу. Тот предложил незамедлительно отправить работу Джону Коллинзу, члену Лондонского королевского общества, который занимался обработкой почты, распространением результатов и новостей подобно Марену Мерсенну. Ньютона охватил нездоровый страх, который будет сопровождать его перед публикацией всех его трудов: обнародовать труд означало подставить его под удары критиков. Здесь следует отметить, чтобы отчасти прояснить причины полемики Ньютона и Лейбница, что в те годы понятие «публикация» имело несколько иной смысл, нежели в наши дни. Сегодня это означает публикацию в научных журналах или в виде книги, доступной всем желающим. В то время, когда книги и особенно журналы еще не набрали такую популярность, как всего несколько десятилетий спустя, публикация означала представление рукописи группе близких друзей, а также тем, кто занимался распространением научных трудов, как, например, Джон Коллинз или в особенности Марен Мерсенн.
Чтобы продемонстрировать опасения Ньютона, далее мы подробно расскажем о письмах, которые Барроу отправил Коллинзу. Сначала, 20 июля 1669 года Ньютон разрешил Барроу всего лишь уведомить Коллинза, что у него находится рукопись «Анализа», запретив упоминать имя автора и название работы: «Один мой друг, обладающий блестящими способностями, отправил мне позавчера несколько писем, в которых описывает метод вычисления размерностей величин, подобный методу Меркатора, но намного более общий применительно к решению уравнений. Я отправлю вам рукопись с одним из ближайших писем и верю, что она доставит вам удовольствие».
Одиннадцать дней спустя Ньютон разрешил Барроу отправить Коллинзу копию «Анализа» при условии, что имя автора будет сохранено в тайне, а рукопись будет возвращена. Обратите внимание, как деликатно Барроу указывает, что Коллинз может ознакомиться с рукописью, но делать копию не следует, иными словами, рукопись предназначена только для Коллинза: «Отправляю вам обещанные письма моего друга, которые, как я надеюсь, доставят вам немалое удовольствие. Я прошу, чтобы вы вернули мне письма, когда сочтете нужным, после того как прочитаете их. Мой друг согласился передать мне письма только на этих условиях, когда я впервые спросил его разрешения отправить их вам. Поэтому прошу вас как можно скорее дать мне знать, что вы получили их, чтобы избавить меня от беспокойства. Чтобы вы могли как можно раньше ознакомиться с ними, я ни минуты не думал о том, чтобы послать их вам обычной почтой».
Когда Коллинз ознакомился с «Анализом» и передал восторженный отзыв Барроу, Ньютон позволил сообщить Коллинзу свое имя, а также разрешил передать рукопись другим: «Я рад, что письма моего друга доставили вам удовольствие. Имя этого юноши — Ньютон, он член нашего колледжа, обладает великолепными способностями и добился в этом вопросе потрясающих успехов. Передайте письма, если пожелаете, достопочтенному господину Броункеру». (Лорд Броункер в то время был главой Лондонского королевского общества.) Вестфолл комментирует: «Это наглядно показывает, что Ньютон, ведущий математик Европы, боялся публиковать свою работу».
Отсюда следует, что площадь, ограниченная кривой у = х2, равна 2/3 ∙ 3/2 x. Может показаться, что Ньютон пытался вычислить площадь, ограниченную кривыми определенного типа, но в действительности полученный им результат намного важнее. В первой части «Анализа» Ньютон хотел изложить общий алгоритм и подчеркнуть, что он применим не только в задачах расчета площади, «Все задачи о длине кривых, о величинах и о поверхностях тел и о центрах тяжести могут быть сведены в конце концов к определению плоской поверхности, ограниченной кривой», — делает он крайне важное замечание, за которым следует раздел под названием «Приложение вышеизложенного к другим примерам того же рода». Это замечание отделяет первую часть работы, в которой изложен общий метод, от второй, в которой излагаются различные способы его применения. Можно сказать, что результат его работы несколько неопределен: Ньютон видел огромную ценность найденного им абстрактного метода, однако, возможно, на начальном этапе, когда идея еще не оформилась окончательно, ему было сложно выразить ее доступно. Скорее всего, на этом этапе ему попросту не хватало терминов и обозначений. Он сосредоточил основное внимание на абстрактной задаче определения функции по известной производной. Кроме того, он рассматривает и обратную задачу о вычислении изменения функции (об этом рассказывается в конце книги). Наконец, он приводит краткий алгоритм расчета этого изменения (производной). Четкие правила вычисления производной позднее опубликовал Лейбниц, но не будем забывать, что в «Анализе» Ньютон изложил не все результаты, полученные им в области математического анализа к 1669 году.
Всё вышеизложенное позволяет заявить, что выход «Анализа» ознаменовал появление анализа бесконечно малых. «Анализ с помощью уравнений с бесконечным числом членов» — великолепный пример, позволяющий оценить акт творения в математике во всем его великолепии: при прочтении книги Ньютона мы становимся свидетелями процесса возникновения анализа бесконечно малых. Так, если мы углубимся в чтение «Анализа» и попытаемся увидеть уже известные нам термины и понятия современного математического анализа, это можно будет сравнить с просмотром детских фотографий человека, с которым мы познакомились уже в зрелом возрасте: сквозь еще не оформившиеся, детские черты уже проступает облик знакомого нам взрослого человека.
Закончив рукопись «Анализа», который принес автору известность среди британских математиков, Ньютон показал свой труд Барроу. Тот предложил незамедлительно отправить работу Джону Коллинзу, члену Лондонского королевского общества, который занимался обработкой почты, распространением результатов и новостей подобно Марену Мерсенну. Ньютона охватил нездоровый страх, который будет сопровождать его перед публикацией всех его трудов: обнародовать труд означало подставить его под удары критиков. Здесь следует отметить, чтобы отчасти прояснить причины полемики Ньютона и Лейбница, что в те годы понятие «публикация» имело несколько иной смысл, нежели в наши дни. Сегодня это означает публикацию в научных журналах или в виде книги, доступной всем желающим. В то время, когда книги и особенно журналы еще не набрали такую популярность, как всего несколько десятилетий спустя, публикация означала представление рукописи группе близких друзей, а также тем, кто занимался распространением научных трудов, как, например, Джон Коллинз или в особенности Марен Мерсенн.
Чтобы продемонстрировать опасения Ньютона, далее мы подробно расскажем о письмах, которые Барроу отправил Коллинзу. Сначала, 20 июля 1669 года Ньютон разрешил Барроу всего лишь уведомить Коллинза, что у него находится рукопись «Анализа», запретив упоминать имя автора и название работы: «Один мой друг, обладающий блестящими способностями, отправил мне позавчера несколько писем, в которых описывает метод вычисления размерностей величин, подобный методу Меркатора, но намного более общий применительно к решению уравнений. Я отправлю вам рукопись с одним из ближайших писем и верю, что она доставит вам удовольствие».
Одиннадцать дней спустя Ньютон разрешил Барроу отправить Коллинзу копию «Анализа» при условии, что имя автора будет сохранено в тайне, а рукопись будет возвращена. Обратите внимание, как деликатно Барроу указывает, что Коллинз может ознакомиться с рукописью, но делать копию не следует, иными словами, рукопись предназначена только для Коллинза: «Отправляю вам обещанные письма моего друга, которые, как я надеюсь, доставят вам немалое удовольствие. Я прошу, чтобы вы вернули мне письма, когда сочтете нужным, после того как прочитаете их. Мой друг согласился передать мне письма только на этих условиях, когда я впервые спросил его разрешения отправить их вам. Поэтому прошу вас как можно скорее дать мне знать, что вы получили их, чтобы избавить меня от беспокойства. Чтобы вы могли как можно раньше ознакомиться с ними, я ни минуты не думал о том, чтобы послать их вам обычной почтой».
Когда Коллинз ознакомился с «Анализом» и передал восторженный отзыв Барроу, Ньютон позволил сообщить Коллинзу свое имя, а также разрешил передать рукопись другим: «Я рад, что письма моего друга доставили вам удовольствие. Имя этого юноши — Ньютон, он член нашего колледжа, обладает великолепными способностями и добился в этом вопросе потрясающих успехов. Передайте письма, если пожелаете, достопочтенному господину Броункеру». (Лорд Броункер в то время был главой Лондонского королевского общества.) Вестфолл комментирует: «Это наглядно показывает, что Ньютон, ведущий математик Европы, боялся публиковать свою работу».
ВЕРСИЯ НЬЮТОНА
Следует привести и другую версию этой истории, автором которой является сам Ньютон. Она изложена в Epistolae posterior- втором письме, которое Ньютон отправил Лейбницу. Письмо содержит немало автобиографических фрагментов. Вот цитата из него: «Когда появилась блестящая книга Logarithmotechnia Николаса Меркатора, я стал уделять этим вопросам [степенным рядам и анализу флюксий] меньше внимания, подозревая, что Меркатору был хорошо известен способ разложения в степенной ряд путем извлечения корней, равно как и разложение в ряд с помощью дробей, либо же другие обнаружат, как это делается, до того как я вступлю в возраст, достойный написания подобного труда. В тот самый момент, когда появилась эта книга, краткое изложение этого метода рядов было сообщено господином Барроу господину Коллинзу. В этом изложении указывались площади и длины кривых, поверхности и объемы тел, составленных из линий, а также способы нахождения этих линий по известным свойствам фигур. Этот метод я ранее проиллюстрировал на примере различных рядов».
Коллинз вскоре вернул рукопись «Анализа» Ньютону через Барроу, однако прежде переписал ее от руки. Эту копию вместе с письмами Барроу обнаружил Уильям Джонс среди документов Коллинза, приобретенных в 1708 году. Увидев эту копию, Джонс предложил Ньютону опубликовать «Анализ». Книга увидела свет в 1711 году. Когда же разгорелся спор о том, кто является истинным первооткрывателем анализа, эти бумаги послужили доказательством первенства Ньютона. Как указывает Вестфолл, «Анализ» оказал большое влияние на карьеру Ньютона. Возможно, именно благодаря публикации этого труда он получил пост лукасовского профессора. Эта должность была создана в Кембридже Генри Лукасом. Стипендия, учрежденная Лукасом для тех, кто занимал эту должность, сделала ее одной из самых престижных в научном мире. В то время эта должность была единственной из восьми существовавших профессорских должностей по направлению математики и натурфилософии, если говорить современным языком. Профессор, занимавший этот пост, должен был вести курсы по геометрии, астрономии, географии, оптике, статике и другим математическим дисциплинам, а также ежегодно передавать в университетскую библиотеку тексты минимум десяти своих докладов. При невыполнении этих условий полагался штраф. Однако Ньютон, который нарушал их достаточно часто, по-видимому, никогда не был оштрафован. Летом 1669 года Барроу, занимавший этот пост уже пять лет с момента его учреждения, начал подумывать об отставке. Скорее всего, он не был очарован гениальностью Ньютона (хотя иногда утверждают обратное), его решение было продиктовано другими причинами. Барроу был не только математиком, но и богословом и хотел последовать своему призванию. Кроме этого, он также хотел получить более влиятельный пост. Спустя год после отставки он получил место капеллана, а два года спустя возглавил Тринити-колледж. Совмещать должность главы колледжа и лукасовского профессора запрещалось, хотя Барроу вполне мог получить разрешение милостью короля. Как бы то ни было, Барроу ушел в отставку, и 29 октября 1669 года по его предложению Ньютон был провозглашен лукасовским профессором. Остаток 1669 года Коллинз и Барроу занимались тем, что уговаривали Ньютона опубликовать «Анализ». Однако они не преуспели в этом, и, как пишет Вестфолл, имея в виду спор с Лейбницем, «нерешительность Ньютона посеяла зерна ожесточенной вражды». Вторая работа Ньютона, его главный труд о бесконечно малых «Метод флюксий» (De methodis serierum et fluxionum), была написана два года спустя, но опубликована лишь в 1736 году. В этой книге Ньютон представляет понятие флюенты — величины, изменяющейся в зависимости от времени, и флюксии флюента — производной этой величины по времени. Вот что он пишет об этих понятиях: «Величины, которые я рассматриваю как постепенно и неопределенно возрастающие; обозначать я их буду последними буквами алфавита: v, х, у, z, чтобы их было возможно отличать от других величин, которые рассматриваются в уравнениях как известные и определенные и которые поэтому обозначаются первыми буквами алфавита a, b, c и так далее. Скорости, с которыми возрастают вследствие порождающего их движения отдельные флюэнты (и которые я называю флюксиями, или просто скоростями, или быстротами), я буду обозначать теми же буквами, но пунктированными: Важно отметить, что Ньютон представил понятия флюенты и флюксии по отдельности как часть теории и привел алгоритмические правила, с помощью которых можно было легко вычислить флюксию флюента. Затем он применил свою теорию для решения задач о касательных, квадратурах, максимумах и минимумах. Как мы уже упоминали, именно благодаря этому Ньютон стал считаться одним из создателей математического анализа. Так, для решения задач о максимумах и минимумах он предложил следующий способ: «Когда величина есть возможно наибольшая или возможно наименьшая, то в этот момент времени она не течет ни вперед, ни назад. Действительно, если бы она могла еще течь вперед, то есть возрастать, то это значит, что до того она наверняка была меньше, чем стала, а после того станет больше, чем она есть. Дело обстояло бы обратным образом, если бы она текла назад или убывала. Поэтому найди ее флюксию согласно проблеме I и положи ее равной нулю». Это знакомый нам способ вычисления производной функции и приравнивания ее к нулю. О задачах расчета квадратуры он писал: «Проблема IX: определить площадь какой-либо заданной кривой. Решение этой проблемы зависит от определения отношения флюент по заданному отношению флюксий». Иными словами, речь идет о процессе, обратном вычислению флюксии; если говорить современным языком — о процессе, обратном вычислению производной, то есть о нахождении первообразной. Здесь Ньютон, по сути, излагает основную теорему анализа и указывает, что ее можно применять для решения задач о площадях. Чтобы доказать мощь своего анализа бесконечно малых, в «Методе» Ньютон использует его для решения практически всех задач о площадях, касательных и многих других, на решение которых его предшественники потратили без малого столетие. Однако «Метод» был опубликован лишь спустя несколько лет после смерти Ньютона. Почему он так долго не давал разрешение на публикацию своих первых книг об анализе бесконечно малых? Мы уже упоминали, что Ньютон не желал публиковать свои результаты из-за особенностей своего характера. В итоге это спровоцировало ожесточенные споры, которых можно было бы избежать, если бы его первые труды были опубликованы без промедления. Нежелание Ньютона публиковать свои работы о математическом анализе было сильно еще и потому, что он осознавал его недостаточную логическую строгость. Понятие флюксии и правила ее вычисления, равно как и дифференциал Лейбница или многочисленные методы работы с бесконечно малыми, предложенные его предшественниками, основывались на так называемых бесконечно малых величинах. Эти «бесконечно малые» представляли собой бесконечно малые числа, практически равные нулю, за счет чего их можно было сокращать при необходимости. В то же время эти величины можно было использовать в знаменателях дробей, так как они не были строго равны нулю. Ньютон безуспешно пытался избежать их и в одной из работ по анализу, «Рассуждении о квадратуре кривых» (De quadratura curvarum), опубликованной в 1704 году как приложение к его же «Оптике», он вплотную подошел к открытию предела, использовав «исчезающие приращения». Это понятие было введено лишь в XIX веке, и Бернард Больцано и Огюстен Луи Коши использовали его как основу анализа бесконечно малых.

Литографический портрет Огюстена Луи Коши, одного из самых плодовитых математиков всех времен.
Ньютон осознавал, что его вычисление флюксий стоит на непрочном логическом фундаменте, поэтому особенно противился публикации любых трудов по этой теме, хотя копии этих рукописей всегда были доступны кругу его друзей. Этот страх, несомненно, оказал влияние и на подготовку его важнейшей работы — «Начал». Ньютон сделал выбор в пользу геометрического языка в древнегреческом стиле, который был менее понятным, но более строгим с логической точки зрения. Он исключил почти все упоминания об анализе бесконечно малых, который, возможно, использовал для получения части результатов, изложенных в «Началах». Тем не менее в «Началах» содержатся отрывочные упоминания о математическом анализе. Таким образом, в этой книге впервые, пусть и косвенно, упоминается анализ бесконечно малых, созданный Ньютоном. Это произошло в 1687 году — спустя три года после того, как Лейбниц опубликовал в журнале Acta eruditorum свою первую статью о дифференциальном исчислении. В лемме II раздела II 2-й книги несколько туманно упоминаются правила, аналогичные современным правилам вычисления производной произведений и степеней. Ньютон применил математический трюк, чтобы избежать сокращения приращений. Этот трюк в середине XVIII века разоблачил Джордж Беркли, который возглавил «крестовый поход» против бесконечно малых. «Начала» вошли в историю математического анализа не только благодаря этой лемме. К математическому анализу можно отнести и другие утверждения, о которых мы расскажем чуть позже, когда будем говорить об ожесточенном споре между Ньютоном и Лейбницем за право называться создателем исчисления.ПРОИЗВОДНАЯ ПО НЬЮТОНУ
В «Началах» Ньютон приводит следующее доказательство правила нахождения производной произведения функций: «Любой прямоугольник, например АВ, увеличенный на непрерывную флюенту, если вычесть из сторон А и В половины их моментов а и b [под моментами понимаются приращения], будет равен:
 или
или

Поскольку стороны А и В увеличиваются на другую половину моментов, прямоугольник превратится в:
 или
или

Вычтем из этого прямоугольника предыдущий прямоугольник и получим излишек aВ + bА. Следовательно, приращение aВ + bА прямоугольника генерируется общими приращениями сторон а и b. Что и требовалось доказать». Если мы запишем приращение А как dА, а приращение В — как dB (Ньютон решительно воспротивился бы использованию подобных обозначений, так как их использовал его противник Лейбниц), то получим знакомое нам правило вычисления производной произведения: d(АВ) = AdB + BdA.
Мы уже упоминали, что Ньютон ссылался на открытую им в самый знаменательный период его жизни теорему о биноме, то есть о разложении (1 + x)m/n в степенной ряд. Однако она стала достоянием общественности лишь десять лет спустя, в 1676 году, причем в сокращенном виде. Ньютон упомянул о ней в первом из двух писем, отправленных Лейбницу через секретаря Лондонского королевского общества Генри Ольденбурга. В этом письме, озаглавленном Epistolae prior, Ньютон, отвечая на вопросы Лейбница, изложил свою теорему о биноме и другие результаты, касающиеся рядов. Теорема о биноме легла в основу созданного им анализа бесконечно малых. По сути, именно с помощью бинома Ньютон разложил в ряд большинство элементарных функций: обратных тригонометрических (их производные можно найти с помощью бинома), а на их основе и тригонометрических функций. Аналогично он вычислил производные логарифмических и показательных функций. Некоторые из полученных результатов уже были известны. Разложение в ряд для логарифмической функции впервые приводится в уже упоминавшейся книге Николаса Меркатора Logarithmotechnia (1668).
Высокомерный гений
Ньютон никогда не был склонен благодарить других за вклад в его открытия, однако требовал от остальных признания того, чем якобы они были обязаны ему. Ньютону нередко приписывают такую фразу: «Если я видел дальше других, то потому, что стоял на плечах гигантов», которую считают выражением благодарности и признанием заслуг других ученых. Эта фраза содержится в одном из писем Ньютона к Гуку, датируемом 1676 годом. Эти письма помогли хотя бы формально уладить разногласия в споре о природе света и цветов. Цитата Ньютона восходит к Иоанну Солсберийскому, который в своем трактате «Металогик» (1159) цитирует Бернара Шартрского: «Мы подобны карликам, стоящим на плечах гигантов: мы видим больше и смотрим дальше не потому, что наше зрение острее, и не потому, что мы выше, а потому, что можем забраться высоко благодаря росту гигантов». Эту фразу можно считать выражением благодарности Ньютона Гуку, на плечи которого, фигурально выражаясь, забрался Ньютон, чтобы видеть дальше. Однако возможна и другая, более замысловатая трактовка, которую приводит Ф. Мэнюэль и в основе которой лежит тот факт, что Роберт Гук был низкорослым и горбатым: «5 февраля 1676 года Ньютон ответил избитой фразой, часто упоминавшейся в спорах о прогрессе, которая восходит как минимум к Иоанну Солсберийскому и часто приводится вне контекста как признание заслуг предшественников Ньютона: “Если я видел дальше других, то потому, что стоял на плечах гигантов”. Если рассматривать эту фразу в контексте и учитывать психологическую атмосферу переписки 1676 года, то эта цитата выглядит сложной и даже неоднозначной. <…> Явно не упоминаемый образ карлика, который взобрался на плечи гиганта, выглядит не вполне прилично. Эта фраза со стороны Ньютона, обращенная к Гуку, выглядит издевательской аналогией. На первый взгляд может показаться, что Ньютон сравнивает Гука с гигантом, а себя считает карликом по сравнению с ним. Однако эта фраза относилась к низкорослому и горбатому человеку, поэтому Ньютон насмехается над ним, вольно или невольно». Вестфолл не разделяет взгляда Мэнюэля и считает, что Ньютон не допускал себе столь резких нападок на оппонентов: «Когда он нападал, то склонял голову и выдвигал обвинения прямо». Еще одно доказательство нежелания Ньютона признавать, что он научился чему-то у других, прослеживается в его отношениях с Декартом. Именно у Декарта он научился аналитической геометрии, сыгравшей важнейшую роль в создании анализа бесконечно малых. Несмотря на это, Ньютон говорил, что испытывает глубокую неприязнь к французскому ученому. Когда Ньютон перечитывал «Геометрию» Декарта примерно в 1680 году, он заполнил поля пометками «осуждаю», «ошибка», «это не геометрия». Он даже написал черновик статьи под названием «Ошибки в «Геометрии» Декарта» (Errors in Descartes’ Geometry). Он называл аналитическую геометрию «языком мошенников от математики». В 1684 году Ньютон оставил про пуск в том месте рукописи, где должно было упоминаться имя Декарта, словно хотел забыть обо всем, чему научился у него: «Я размышлял над этими вопросами около девятнадцати лет, сравнивая между собой открытия и Худде».Жизнь в Лондоне, служба на Монетном дворе
Ньютон сменил Кембридж на Лондон в 1696 году, став сначала смотрителем, а затем управляющим («мастером») Монетного двора. Широко известна колкая фраза Вольтера из «Философских писем»: «В юности я думал, что причиной богатства Ньютона были его огромные заслуги. Я предполагал, что он был назначен мастером Монетного двора в знак признания. Ничего подобного. У Исаака Ньютона была очаровательная племянница, мадам Кондуит. Она чрезвычайно нравилась министру финансов графу Галифаксу. Открытие анализа бесконечно малых и закона всемирного тяготения не помогли бы ему, если бы не его прекрасная племянница».
Сохранились различные портреты Ньютона, а также маски и бюсты.
На иллюстрации представлены два из многочисленных портретов кисти художника Готфрида Кнеллера. Слева изображен портрет Ньютона в возрасте 46 лет, спустя некоторое время после публикации «Начал», справа — в возрасте 59 лет, когда он уже был мастером Монетного двора.
Вольтер либо преувеличил слухи, либо был не слишком осведомлен о сути дела, поскольку на момент назначения Ньютона на должность его племяннице было всего 17 лет, и, возможно, она никогда не встречалась с лордом Галифаксом. Однако позднее между ними действительно возникла тесная дружба, и после смерти Галифакса в 1714 году племянница Ньютона получила в наследство целое состояние, как написал Галифакс в завещании, «в знак искренней любви, привязанности и уважения, которое вы испытывали ко мне столь длительное время, и в качестве небольшой компенсации за удовольствие и радость, доставленные беседами с вами». Ньютон был строгим мастером Монетного двора и вложил в работу весь свой великолепный ум, невероятную работоспособность, применив, несомненно, обширный опыт, полученный при проведении экспериментов по алхимии. Это не могло понравиться фальшивомонетчикам, которых Ньютон безжалостно преследовал. Спустя несколько лет после того, как он поступил на службу в Монетный двор, научный мир и общество выразили ему еще большую признательность: в 1703 году Ньютон был избран президентом Королевского общества, которым он управлял подобно абсолютному монарху, а в 1705 году королева Анна произвела его в рыцари в Кембриджском Тринити-колледже.Ньютон и его друзья
Портрет Ньютона будет неполным, если мы не упомянем о его отношениях с друзьями и близкими. Быть может, причиной тому, что Ньютон тяжело сходился с людьми, был его непростой характер. Правда, в последние годы, прожитые в Лондоне, он пользовался славой гостеприимного хозяина — возможно, гости попадали под очарование его племянницы. Должно быть, поэтому в юности, точнее в 1660—1670-е годы, Ньютон, родившийся в 1642 году, поддерживал близкие отношения преимущественно с теми, кто был старше него. Например, Генри Мор родился в 1614 году, Джон Валлис — в 1616-м, Джон Коллинз — в 1624-м, Генри Ольденбург — в 1626-м, Исаак Барроу — в 1630-м, Кристофер Рен — в 1632-м. Среди всех друзей его ровесниками были едва ли несколько человек. Кроме того, дружеские отношения осложняло крайнее пуританство Ньютона: он прекратил общение с итальянцем Джоном Вигани, преподававшим в Кембридже химию, так как тот ввязался в неприятную историю с монахиней. Обратите внимание: все ученые, с которыми он вел наиболее жаркие споры, принадлежали к его же поколению: Роберт Гук родился в 1635 году, Лейбниц — в 1645-м, Джон Флемстид — в 1646-м. Эти противостояния имели различный характер — так, причиной споров с Гуком и Лейбницем были вопросы первенства и обвинения в плагиате, — но все они были грубыми и жесткими. Они показывают, сколь несправедлив и властен был порой Ньютон в последние годы жизни, когда добился признания и почестей. Вот как описывает Ф. Мэнюэль противостояние Ньютона и Гука: «Когда две масштабные личности сталкивались в тесных научных кругах XVII века, неизбежно возникали стычки. В Королевском обществе не было места для Ньютона и Гука одновременно. Первенство могло принадлежать только кому-то одному из них. Ньютон вторгся в царство, где когда-то безраздельно властвовал Гук, и, когда на небосклоне взошла его звезда, Гук лишился власти и статуса. Он сражался за свое место, принижая достижения новичка, обвиняя того в плагиате, прочно удерживая свой пост до самой смерти в 1703 году. Лишь тогда Ньютон занял пост президента Королевского общества, став непререкаемым лидером в научных кругах». В зрелые годы (с 1680 года и далее) Ньютон, напротив, сблизился с более молодыми коллегами: Абрахамом де Муавром, который родился в 1667 году, Никола Фатио де Дюилье (в 1664-м), Дэвидом Грегори (в 1659-м) и Эдмундом Галлеем (в 1656-м). Почти все они находились под покровительством Ньютона, который расставил их на посты глав кафедр британских университетов в первые годы XVIII века. Ф. Мэнюэль усматривает в дружбе Ньютона с юными и талантливыми учеными фрейдистский подтекст: «Ньютон в первую очередь отождествлял себя с личностью своей матери и представлял сексуальный объект сам для себя. Когда он встретился с юношами, похожими на него, он полюбил их так, как хотел, чтобы его любила мать». Следует особо выделить Никола Фатио де Дюилье, так как он сыграл особую роль в полемике с Лейбницем.НИКОЛА ФАТИО ДЕ ДЮИЛЬЕ (1664-1753)

Никола Фатио де Дюилье родился в Базеле в 1664 году. Его первым увлечением стала астрономия, и некоторое время он посещал занятия в Парижской обсерватории вместе с Кассини. Ему не удалось получить членство во Французской академии наук, и он отправился в Голландию, где в 1686 году познакомился с Гюйгенсом, который посоветовал ему заняться математикой. Примерно в 1687 году уже в Англии Фатио завершил свою версию анализа бесконечно малых, не столь полную, как варианты Ньютона и Лейбница. В течение последующих лет он был близким другом Ньютона. Однако в 1706 году он сблизился с кальвинистами Лангедока, которые нашли убежище в Англии, и занял место секретаря в их организации. Фатио попал в немилость: ему было предложено покинуть Англию и тем самым избежать насмешек, но он предпочел разделить судьбу своих единомышленников. Он лишился благосклонности не только Ньютона, но и почти всего европейского научного сообщества. Неприязненное отношение к нему сохранялось еще почти полвека, до самой его смерти.
Фатио прибыл в Англию весной 1687 года, накануне публикации «Начал», с которыми были связаны большие ожидания в научных кругах. Он тут же попал под влияние новой натурфилософии,изложенной в «Началах», и выразил сильную привязанность к автору, которая оказалась взаимной. Знакомство состоялось в 1689 году: этим годом датированы первые письма, которые Ньютон отправил Фатио. Практически все исследователи биографии Ньютона отмечают необычный тон его писем: привязанность и теплота, которой наполнены строки, не встречаются ни в каких других его письмах. Их отношения стали особенно близкими в конце 1692 — начале 1693 года, после того как Фатио несколько раз переболел лихорадкой, что едва не стоило ему жизни, о чем он сообщил в письме Ньютону в сентябре 1692 года. Ньютон предложил ему деньги и пригласил поселиться у него в кембриджском Тринити-колледже. Фатио отказался и, оправившись от болезни, в 1693 году поехал в Швейцарию, чтобы уладить дела с наследством. Ньютон пережил крупный кризис летом того же года. Логично задаться вопросом, был ли этот кризис вызван размолвкой с Фатио. О причинах и обстоятельствах болезни Ньютона существует множество гипотез. Возможно, причиной стало перенапряжение и усталость, накопившиеся за время работы над «Началами»; может быть, отравление ртутью, вызванное экспериментами по алхимии: в волосах, предположительно принадлежавших Ньютону, была обнаружена необычайно высокая концентрация ртути; однако были получены неопровержимые доказательства, свидетельствующие не в пользу этой гипотезы. Возможно, причиной была обычная депрессия. Думается, что сказалось влияние всех вышеперечисленных причин, включая, разумеется, размолвку с Фатио де Дюилье, которая пришлась как раз на этот период. Именно этой гипотезе отдает предпочтение Фрэнк Мэнюэль, указывая на их возможную платоническую связь. Однако это открыто отрицают другие исследователи биографии Ньютона, в частности Уайтсайд. Как бы то ни было, в 1693 году между друзьями произошла размолвка, и отношения Ньютона и Фатио больше никогда не были столь близкими, как в период с 1689 по 1693 год. Тем не менее впоследствии Фатио иногда вновь появлялся в жизни Ньютона. Так, в 1699 году он первым публично обвинил Лейбница в заимствовании анализа бесконечно малых у Ньютона.
Похороны Ньютона
«Тот, кто гением превзошел род человеческий», величайший ученый, по мнению Гаусса, умер 20 марта 1727 года в Лондоне. Вольтер писал: «Он жил, почитаемый соотечественниками, и был погребен подобно королю, который делал добро своим подданным». Или, как пишет, подражая стилю Вольтера, Фернандо Саватер в «Саду сомнений»: «…был особенно впечатлен траурной церемонией по случаю похорон Ньютона. В них участвовал весь Лондон. Сначала тело было выставлено на всеобщее обозрение в пышном катафалке, по бокам которого горели огромные светильники, затем было перенесено в Вестминстерское аббатство, где Ньютон был похоронен среди королей и выдающихся государственных деятелей. Во главе траурной процессии шел лорд-канцлер, за которым следовали все королевские министры».
Могила Ньютона в Вестминстерском аббатстве.
Глава 4. Лейбниц, мастер на все руки
Ньютон оставил после себя множество отредактированных рукописей. Лейбниц не только не отстал от него в этом, но и превзошел: его корреспонденция была намного более объемной. Рукописи Лейбница ждала более завидная участь, чем бумаги Ньютона: они не были проданы с аукциона, а более или менее систематическое их изучение с последующей публикацией было начато почти на сто лет раньше. Однако исследования творчества Лейбница никогда не были столь интенсивными и не принесли столь удивительных результатов, как те, что были выполнены исследователями биографии Ньютона после Второй мировой войны. Решающий шаг к изданию полного собрания рукописей и писем Лейбница был сделан лишь в XX веке на первом заседании Международной ассоциации академий наук, прошедшем в Париже. Это издание готовится до сих пор, с перерывами, вызванными двумя мировыми войнами, и все еще достаточно далеко от завершения. Из восьми серий собрания сочинений и писем Лейбница три первых полностью отведены под корреспонденцию. Лейбниц состоял в переписке более чем с 600 адресатами, среди которых было множество политиков, ученых и философов того времени, а вся его корреспонденция насчитывает примерно 20000 писем: половина написана им самим, а остальные принадлежат его адресатам. (Для сравнения: семь томов переписки Ньютона содержат всего 1600 писем.) Сохранилось большинство этих писем, по меньшей мере в виде черновиков или выписок, поскольку Лейбниц, так же как и Ньютон, никогда не выбрасывал своих бумаг. Изучение рукописей Лейбница не изменило представлений об этом гениальном немецком ученом (как произошло в случае с Ньютоном), однако некоторые аспекты его трудов прояснились. По мнению Бертрана Рассела, бумаги Лейбница показывают нам лучшее из его философии: материалы, которые не предназначались для чтения в высшем обществе или для заработка и поэтому остались под сукном. В частности, бумаги Лейбница помогли увидеть, как он пришел к открытию анализа бесконечно малых. Стало понятно, что он совершил свое открытие независимо от Ньютона. Лейбниц внес вклад в самые разные области науки, и это доказывает то, что было известно еще его современникам: он был мастером на все руки или, как указано в Энциклопедии Британника, «одним из величайших дарований западной цивилизации». В современном мире всеобщей узкой специализации особенно выделяется ученый, подобный Лейбницу, который хотел знать всё и обо всем, будь то наиболее уважаемые в то время науки — философия, физика, метафизика, математика — или другие области, очевидно более далекие от кабинетных размышлений — постройка гидравлических прессов, дренаж шахт с помощью ветряных мельниц, геология и изготовление тканей из льна. Однако в этом стремлении понять всё и высказать обо всем свое мнение, пусть не всегда глубокомысленное, прослеживаются некоторые центральные идеи. Одна из таких идей — поиск characteristica universalis, универсального языка, который должен быть символьным, четким и однозначным, а также ars combinatoria — системы рассуждений. Эта система, согласно Лейбницу, позволяла «производить столь же осязаемые рассуждения, что и математические, вследствие чего обнаружить ошибку можно будет невооруженным глазом, и в случае диспута мы сможем сказать “произведем вычисления”, чтобы узнать, кто же прав». Именно его версия анализа бесконечно малых, полная превосходных обозначений, математический вариант characteristica universalis, позволила упорядочить неисчислимое множество результатов, связанных с квадратурами, касательными, максимумами и минимумами, центрами тяжести и так далее. Об универсальности говорится в статьях, написанных Лейбницем в конце жизни, где он признает, что в конечном итоге его вкладом в анализ бесконечно малых стало создание языка, позволившего найти единообразное решение множества задач, которые ранее решались совершенно разными способами. Его тяга к всеобщей гармонии выразилась в желании объединить христианские церкви и создать одно государство из множества немецких земель. Правда, истинной причиной этому было стремление выступить сообща, отвечая тем самым на турецкую угрозу». Лейбниц первым попытался примирить католиков и протестантов. Сам он был лютеранином и часто отказывался от заманчивых должностей вроде главы библиотеки Ватикана или поста во Французской академии наук, так как не желал принимать католицизм. Позднее он попытался реализовать более скромный, но столь же невозможный замысел — объединить лютеран и кальвинистов. Для этого он провел большую работу на стыке богословия и дипломатии, не отказывался выслушивать обе стороны, предлагал планы действий и конкретные способы. Сравните это с религиозными воззрениями Ньютона, который в тайне от всех придерживался арианства.
Портрет Лейбница в пышном парике, соответствующем требованиям того времени.
Тем не менее Лейбницу не удалось реализовать задуманное. Однако никакая, даже самая крупная неудача не могла умерить его безграничный оптимизм. Удивительно уже то, что он, рожденный в Германии, опустошенной после Тридцатилетней войны, был оптимистом и написал такие строки в «Опыте теодицеи о благости Бога, свободе человека и происхождении зла»: «Среди бесконечного множества возможных миров лучшим является тот, что существует. Иными словами, Бог не хотел создать ничего другого… и вы находитесь в источнике счастья». Бертран Рассел так объясняет принципы Лейбница: «Пусть в нашем мире и присутствует зло, тем не менее добро в нем преобладает над злом больше, чем в любом другом из возможных миров. Следовательно, наш мир — лучший из возможных, а зло, которое в нем содержится, не противоречит идее о добродетели Бога. Этот аргумент, очевидно, понравился королеве Пруссии. Ее слуги продолжали терпеть зло, в то время как она наслаждалась добром, и ей доставляло удовольствие, что, по мнению великого философа, это было законно и справедливо». Вольтеру не пришлось прибегать к излишним преувеличениям, когда в романе «Кандид» он создал образ учителя Панглосса, карикатуру на Лейбница: «Панглосс был учителем метафизико-теологико-космолонигологии. Он замечательно доказывал, что не бывает следствия без причины и что в этом лучшем из возможных миров замок владетельного барона — прекраснейший из возможных замков, а госпожа баронесса — лучшая из возможных баронесс».
Тома полного собрания сочинений Лейбница, хранящегося в библиотеке бенедиктинского монастыря в Гётвейге в австрийской долине Вахау.
Расскажем в нескольких словах о детстве Лейбница, которое было не столь богатым на травмы, как детство Ньютона. Лейбниц, в отличие от Ньютона, знал своего отца, юриста и преподавателя этики Лейпцигского университета. Мать Лейбница была его третьей женой. Отец Лейбница умер в 1652 году, когда мальчику было всего шесть лет. После отца осталась прекрасная библиотека, в которую Лейбниц был допущен, лишь когда ему исполнилось восемь. С отцовской библиотеки и началось его образование, хотя он также посещал школу. В 1661 году он поступил в Лейпцигский университет, намереваясь изучать юриспруденцию. Пять лет спустя он попытался получить степень доктора, однако ему было отказано: он был слишком молод, и, возможно, определенную роль сыграла неприязнь к нему жены декана факультета. Он перевелся в Альдорфский университет в Нюрнберге, где смог защитить работу о некоторых сложных случаях в юриспруденции. Лейбницу была предложена должность преподавателя, но он отказался. Он никогда не выказывал особенного энтузиазма по поводу университетов (возможно, небезосновательно) и был сторонником создания альтернативных учреждений для развития науки и мысли. В частности, Лейбниц способствовал созданию научного журнала Acta eruditorum в своем родном Лейпциге, а также принимал активное участие в учреждении Берлинской академии наук, президентом которой он был с момента ее основания в 1700 году. Санкт-Петербургская же академия была создана царем Петром I по совету Лейбница уже после смерти ученого. Возможно, в Нюрнберге в 1667 году Лейбниц познакомился со своим первым покровителем, бароном Иоганном Кристианом фон Бойнебургом, который помог ему поступить на службу в Майнце. Благодаря этому Лейбниц в 1672 году смог посетить Париж. Ему было поручено представить двору короля Людовика XIV проект военного союза для последующего нападения на Египет, чтобы отвлечь внимание Франции от голландских земель. Эта миссия по созданию союза двух церквей против неверных могла служить прикрытием для другого, более прозаичного задания: Лейбниц должен был заняться вопросом ренты и пенсиона, которые полагались его покровителю фон Бойнебургу во Франции. Как бы то ни было, Лейбниц пробыл в Париже до октября 1676 года. Это путешествие стало решающим этапом в его обучении многим наукам и, разумеется, математике, так как именно в последние месяцы пребывания в Париже он создал анализ бесконечно малых.Лейбниц и анализ бесконечно малых
«Почти все остальные крупные математики, — писал в XX веке Иозеф Хоффман, видный исследователь биографии Лейбница, — увлекались математикой уже в юные годы и разрабатывали радикально новые идеи. Однако этот период в жизни Лейбница не был ознаменован какими-либо заметными математическими открытиями». И в этом, и во многом другом Лейбниц очень отличается от Ньютона. Когда Лейбниц прибыл в Париж, ему было уже 26 лет. К этому времени он был лишь поверхностно знаком с «Началами» Евклида и знал немногим больше элементарной арифметики, изученной в школе по книге Клавия. Как рассказывал много лет спустя один из его первых учеников Иоганн Бернулли, издание «Геометрии» Декарта с комментариями Ван Схотена, с которым Лейбниц бегло ознакомился в университете, показалось ему слишком сложным. В Нюрнберге, где он жил после получения степени доктора в Альдорфском университете (1666 год), он поверхностно изучил Geometria indivisibilibus Кавальери. Так что, когда он прибыл в Париж в марте 1672 года, его знания были весьма плачевными, хотя, по словам Хоффмана, математика была у Лейбница в крови. Сохранилось множество рукописей и документов Лейбница, в частности почти все, написанное им в период обучения в Париже. Эти документы позволяют понять, как проходило его обучение и как он пришел к открытию анализа бесконечно малых. В первый год в Париже Лейбниц был дилетантом в математике. Позднее он сам признавался, что мучился от недостатка знаний. В этом же году он впервые побывал в Лондоне, где при посредничестве Ольденбурга и Коллинза познакомился с английскими математиками. Его «святая простота», о которой он знал, его недооценка собственных возможностей вкупе с излишней открытостью и общительностью не раз приводили к недопониманию с британскими математиками и впоследствии стали одной из причин обвинений в плагиате. Осенью 1672 года он познакомился с Христианом Гюйгенсом, самым известным ученым и математиком Европы, который в то время получал жалование во Французской академии наук. К тому времени Лейбниц уже совершил свое первое математическое открытие: он показал, как использовать разность для сложения чисел. Позднее он упоминал, что на мысль о взаимно обратной связи дифференцирования и интегрирования его навела взаимно обратная связь между сложением и вычитанием. Рассуждения Лейбница были таковы. Допустим, что требуется найти сумму а1 + а2 + а3 + … + аn. Нам известно, что каждое из этих чисел является разностью двух других: ak = bk+1 — bk. Следовательно, простое сокращение последовательных членов bk означает, что а1 + а2 + а3 + … + аn = bn+1 — b1. Ввиду врожденного оптимизма и недостатка математических знаний Лейбниц посчитал, что открыл способ нахождения суммы произвольных рядов чисел. Его уверенность только усилилась, когда он поделился своим открытием с Гюйгенсом и тот предложил найти сумму чисел, обратных треугольным числам:1/2 + 1/6 + 1/12 + 1/20 + …
По случайному совпадению, этот ряд — один из немногих, к которым применим способ, открытый Лейбницем, так как члены этого ряда имеют вид 1/n(n+1), то есть равны разности между 1/n и 1/(n+1). Таким образом,1/2 + 1/6 + 1/12 + 1/20 + … = 1
Лейбниц вычислил суммы похожих рядов, образованных пирамидальными числами, и подготовил небольшую статью для публикации в Journal des Savants. Однако статья так и не увидела свет, поскольку весь 1673 год журнал не издавался. В этой статье Лейбниц цитирует Кавальери, Галилея, Валлиса, Грегори, Паскаля, Сен-Венсана и Архимеда, а также упоминает Гоббса как великого математика, что указывает на определенный прогресс в его образовании. В январе 1673 года Лейбниц впервые посещает Лондон. Свой первый визит он нанес Генри Ольденбургу, секретарю Лондонского королевского общества и своему соотечественнику, который принял его с распростертыми объятиями.ГЕНРИ ОЛЬДЕНБУРГ (1618-1677)

Ольденбург родился в немецком городе Бремене. О его юности известно очень немногое. Примерно в 1654 году он был уполномочен властями Бремена на выполнение дипломатической миссии в Англии, где в то время правил Оливер Кромвель. С 1654 по 1661 год, когда он был избран членом Лондонского королевского общества, он с перерывами находился в Англии, Ольденбург упоминается как один из секретарей Королевского общества в двух первых письмах короля, датированных 1662 и 1663 годом. Этот пост он занимал в течение 15 лет, вплоть до своей смерти в 1677 году. Он создал полноценную систему архивов и поддерживал переписку со многими учеными Англии и других стран, что позволило ему осуществлять важнейший обмен идеями. Именно через него проходили письма, которыми обменивались Ньютон и Лейбниц в 1676-1677 годах. Их переписка прекратилась со смертью Ольденбурга. Не забывайте, насколько сложным в те годы было поддержание подобных связей: почта в то время где-то не существовала вовсе, где-то работала крайне ненадежно, особенно при передаче писем между странами, находящимися в состоянии войны. Используя дипломатические каналы, Ольденбург создал сеть посредников, которые передавали корреспонденцию, что было особенно ценно во время войны. Подобный шаг был достаточно рискованным: в 1667 году Ольденбург провел несколько месяцев в лондонском Тауэре, возможно, из-за того, что позволил себе «недостаточно патриотичные высказывания» о британских властях в письме к иностранцу.
22 января 1673 года Лейбниц представил Лондонскому королевскому обществу деревянную модель вычислительной машины, способной выполнять сложение, вычитание, умножение и деление. Хотя модель, изготовленная в Париже, была несовершенной, именно за ее создание Лейбниц впоследствии был избран членом Королевского общества. Ольденбург сообщил ему об этом в письме, написанном в апреле того же года, однако два месяца спустя напомнил, что он обещал представить членам общества усовершенствованную модель. Свое обещание Лейбниц выполнил лишь несколько лет спустя.

Лейбниц создал машину, способную умножать числа путем многократного выполнения сложения.
Некоторое время спустя между Лейбницем и Джоном Пеллом произошел инцидент, в котором англичане встали на сторону Пелла. Лейбниц познакомился с Пеллом на встрече с Робертом Бойлем в доме его сестры на улице Пэлл-Мэлл. Как позднее вспоминал Лейбниц, он иногда посещал Бойля, так как «не пренебрегал химией». Лейбниц сообщил Пеллу, что открыл общий метод представления и интерполяции рядов с помощью разностей чисел. Пелл был удивлен: Лейбниц приехал из Парижа и должен был знать, что эти результаты уже были опубликованы во Франции и в Англии несколько лет назад Габриелем Мутоном. Лейбниц на следующий же день ознакомился с книгой Мутона в библиотеке Королевского общества и убедился, что Пелл был совершенно прав. Версия Лейбница была зафиксирована в письме к Ольденбургу от 3 февраля 1673 года, а тот в свою очередь сообщил об этом Ньютону. В итоге спустя 14 лет, когда возник спор о том, кто же первым открыл анализ бесконечно малых, Ньютон, словно желая показать склонность Лейбница к плагиату, писал: «Пелл обвинил Лейбница в том, что тот скопировал метод интерполяции из книги Мутона». В последующие месяцы Ольденбург и Лейбниц обменялись письмами, в которых последний пожаловался на недостаток знаний математики. Как позднее вспоминал Лейбниц, в то время он совершенно не знал геометрии. Например, в апреле 1673 года Лейбниц написал Ольденбургу о результатах, касавшихся сумм чисел, обратных фигурным числам. (Ньютон позднее высмеивал эти результаты, так как они были очень простыми.) Когда Ольденбург сообщил, что эти результаты содержатся в книге Quadrature arithmeticae Пьетро Менголи, Лейбниц ошибочно возразил ему, что метод Менголи применим только для конечных, а не для бесконечных рядов. Изучив подробнее труд Менголи, Лейбниц увидел различие между своими результатами и результатами Менголи: они были получены с помощью разных методов. Ольденбург также выслал Лейбницу результаты, которые Коллинз считал наиболее показательными для британской математики того времени. Эти результаты приводились без доказательств, иногда их было сложно понять, кроме того, при переписывании были допущены ошибки. Так как переписка часто сохранялась в архивах Лондонского королевского общества, целью этих писем было документально зафиксировать первенство английских математиков. Ньютон подробнейшим образом изучил эти письма, чтобы подкрепить обвинения Лейбница в плагиате, хотя Ольденбург отправил Лейбницу не письма Коллинза, а их сокращенный перевод с английского на латынь. Из-за этих сокращений вкупе с ошибками, допущенными при переписывании, письма Ольденбурга было практически невозможно понять. Лейбниц, получив эти письма, решил, что ему следует уделять больше времени и внимания математике и завершить свое образование. Именно тогда его охватила подлинная страсть к математике. Он более чем на год прервал переписку с Ольденбургом и принялся за работу. По словами Хоффмана, «он прекратил отношения с Ольденбургом, чтобы заняться самообразованием и заполнить пробелы в знаниях, которые он с болью осознавал. Их отношения возобновились лишь в конце лета 1674 года. Тогда Лейбниц был уже другим человеком и превосходно разбирался в предмете». Лейбниц позднее писал, что обширным знаниям математики он был обязан наставничеству и примеру Гюйгенса. Следуя советам этого голландского ученого, который в то время благосклонно относился к нему, Лейбниц изучил труды Паскаля, Фабри, Грегори, Сен-Венсана, Декарта и де Слюза, а также Меркатора, книгу которого, Logarithmotechnia, он купил в Лондоне, равно как и Lectiones Барроу. Однако эти работы он изучил лишь несколько лет спустя. С книгами остальных авторов он ознакомился в королевской библиотеке, некоторые приобрел. Одной из таких книг было издание «Геометрии» Декарта под редакцией ван Схотена, которое в период жизни в Нюрнберге показалось Лейбницу слишком сложным. Особенно важным стал труд Паскаля Traite des sinus du quart de cercle, в котором рассказывалось о так называемом характеристическом треугольнике — прямоугольном треугольнике, гипотенуза которого является касательной к кривой, а катеты — дифференциалами x и у, как показано на рисунке.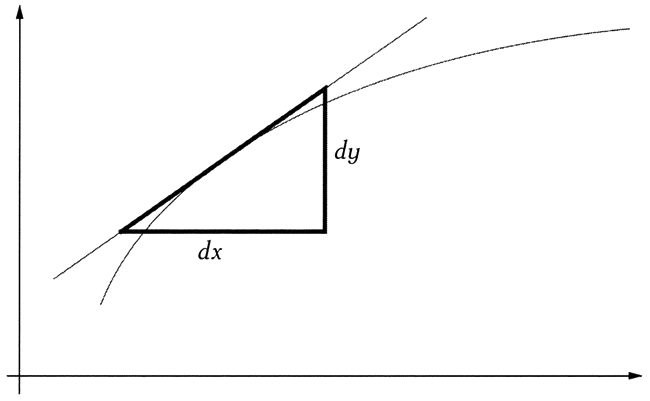 Несколько лет спустя в письме к одному из своих первых учеников Якобу Бернулли Лейбниц написал, что именно эта работа Паскаля со всей ясностью показала ему, что задачи о касательных и квадратурах являются взаимно обратными. Лейбниц добавил, что у Паскаля, должно быть, была повязка на глазах — ничем иным нельзя объяснить то, что он сам не заметил этого. Лейбниц продемонстрировал племяннику Паскаля свою вычислительную машину в июне 1674 года. Паскаль также придумал вычислительную машину, которая, однако, была способна выполнять только сложение и вычитание. Лейбниц выразил сожаление, что некоторые статьи Паскаля были до сих пор не опубликованы, и попросил его племянника отправить ему несколько рукописей этого французского математика и философа.
В течение 1673 года Лейбниц с помощью характеристического треугольника совершил несколько важных открытий. В частности, он открыл метод преобразования, напоминающий современный метод интегрирования по частям. Взяв за основу этот метод, он смог найти разложение в ряд для функции арктангенса и получил свой знаменитый бесконечный ряд, с помощью которого можно вычислить число 71. В декабре 1673 года Лейбниц обсудил с Гюйгенсом возможность решения классической греческой задачи о квадратуре круга с помощью этого ряда.
Далее он занялся решением задач о касательных, взяв за основу метод де Слюза. Хоффман, подробно изучив рукописи Лейбница того периода, сделал вывод, что в своей работе Лейбниц опирался на труды вышеупомянутых авторов, к которым следует добавить Гюйгенса, и не использовал работы Ньютона и Барроу.
В письмах, отправленных во второй половине 1674-го и в начале 1675 года, Лейбниц сообщил Ольденбургу о своих результатах, полученных, по его словам, отчасти «благодаря редкой удаче». В частности, он ознакомил Ольденбурга (не приведя ни подробностей, ни формулы) с рядом для вычисления числа 71, разложением функции арксинуса в ряд, а также косвенно упомянул метод преобразования. На этот раз Ольденбург ответил ему в более критическом тоне, чем в ранний период их знакомства, так как в то время Лейбниц не скрывал своего дилетантства. Также не приводя ни подробностей, ни формул, он сообщил Лейбницу о результатах, полученных британскими математиками, в частности Ньютоном и Джеймсом Грегори: «Мне хотелось бы обратить ваше внимание на то, что теория и метод измерения кривых, которые использует уже упомянутый Джеймс Грегори, а также Исаак Ньютон, могут быть применены к любой кривой, механической или геометрической». В письме от 20 марта 1675 года Лейбниц просит подробнее рассказать об этих результатах.
Ольденбург переадресовал письмо Коллинзу, после чего 12 апреля направил Лейбницу ответ, в котором указывается разложение в ряд для синуса и арксинуса, полученное Ньютоном, ряды Грегори для тангенса и арктангенса, а также некоторые результаты, касающиеся интерполяции, квадратур и других задач. Как бы то ни было, в письме приводились лишь результаты, но не объяснялось, каким способом они были получены. Лейбниц приписал авторство этих рядов Ольденбургу и, по мнению Хоффмана, не совсем понял, что попало ему в руки, так как пообещал сравнить эти результаты со своими и дать по этому поводу комментарий, но так никогда и не сделал этого. Так как о некоторых из этих рядов Лейбниц узнал позднее и из других источников, это дало Ньютону основания впоследствии обвинить его в плагиате результатов, полученных через Ольденбурга.
Мы можем достаточно точно указать, когда Лейбниц открыл анализ бесконечно малых. Это произошло в конце октября — начале ноября 1675 года, если вообще уместно приводить столь точные даты для такого значимого открытия. В сохранившихся рукописях, которые относятся к этому периоду, особенно тех, что датированы 29 октября и 11 ноября, Лейбниц вводит систему обозначений математического анализа и описывает с ее помощью алгоритм, в котором впоследствии станут заметны различия с работами его предшественников, приводит правила анализа и определяет интегрирование и дифференцирование как взаимно обратные операции. Хоффман пишет: «После того как был сделан этот первый, решающий шаг в сторону «алгебраизации» задач о бесконечно малых, перед этим человеком, умевшим определить характерные и общие элементы среди мешанины похожего, открылась новая картина мира. <…> Он четко понимал, чего не хватает в созданном им математическом анализе, но знал, что эти недостатки можно исправить и что путь в новый мир успешно открыт».
Ключевую роль сыграли работы по решению задач поиска кривой по заданной касательной, которыми Лейбниц занимался в октябре 1675 года. За год до этого он решил задачу определения кривой по известной поднормали.
В рукописи, датируемой 29 октября 1675 года, Лейбниц ввел знак ∫ — стилизованную букву S, первую букву латинского слова summa для обозначения суммы бесконечно малых. До этого использовалась аббревиатура omn. — от латинского de omnium («все»), введенная Кавальери. Лейбниц писал: «Будет удобно записывать omn. как ∫, так что ∫l = omn.l, то есть сумма l».
Далее в этой же рукописи он вводит букву d для обозначения дифференциала.
Изначально он поместил это обозначение в знаменатель: «Это получается обратным расчетом. То есть допустим, что ∫l = уа, где l = ya/d. Тогда с ростом ∫d будет уменьшаться в размерах. Однако ∫ означает сумму, a d — разность».
Спустя несколько дней в рукописи, датированной 11 ноября 1675 года, он переместил d в числитель и записал — как dx. В этой же рукописи Лейбниц задается вопросом о равенстве d(xy) и dxdy, а также
Несколько лет спустя в письме к одному из своих первых учеников Якобу Бернулли Лейбниц написал, что именно эта работа Паскаля со всей ясностью показала ему, что задачи о касательных и квадратурах являются взаимно обратными. Лейбниц добавил, что у Паскаля, должно быть, была повязка на глазах — ничем иным нельзя объяснить то, что он сам не заметил этого. Лейбниц продемонстрировал племяннику Паскаля свою вычислительную машину в июне 1674 года. Паскаль также придумал вычислительную машину, которая, однако, была способна выполнять только сложение и вычитание. Лейбниц выразил сожаление, что некоторые статьи Паскаля были до сих пор не опубликованы, и попросил его племянника отправить ему несколько рукописей этого французского математика и философа.
В течение 1673 года Лейбниц с помощью характеристического треугольника совершил несколько важных открытий. В частности, он открыл метод преобразования, напоминающий современный метод интегрирования по частям. Взяв за основу этот метод, он смог найти разложение в ряд для функции арктангенса и получил свой знаменитый бесконечный ряд, с помощью которого можно вычислить число 71. В декабре 1673 года Лейбниц обсудил с Гюйгенсом возможность решения классической греческой задачи о квадратуре круга с помощью этого ряда.
Далее он занялся решением задач о касательных, взяв за основу метод де Слюза. Хоффман, подробно изучив рукописи Лейбница того периода, сделал вывод, что в своей работе Лейбниц опирался на труды вышеупомянутых авторов, к которым следует добавить Гюйгенса, и не использовал работы Ньютона и Барроу.
В письмах, отправленных во второй половине 1674-го и в начале 1675 года, Лейбниц сообщил Ольденбургу о своих результатах, полученных, по его словам, отчасти «благодаря редкой удаче». В частности, он ознакомил Ольденбурга (не приведя ни подробностей, ни формулы) с рядом для вычисления числа 71, разложением функции арксинуса в ряд, а также косвенно упомянул метод преобразования. На этот раз Ольденбург ответил ему в более критическом тоне, чем в ранний период их знакомства, так как в то время Лейбниц не скрывал своего дилетантства. Также не приводя ни подробностей, ни формул, он сообщил Лейбницу о результатах, полученных британскими математиками, в частности Ньютоном и Джеймсом Грегори: «Мне хотелось бы обратить ваше внимание на то, что теория и метод измерения кривых, которые использует уже упомянутый Джеймс Грегори, а также Исаак Ньютон, могут быть применены к любой кривой, механической или геометрической». В письме от 20 марта 1675 года Лейбниц просит подробнее рассказать об этих результатах.
Ольденбург переадресовал письмо Коллинзу, после чего 12 апреля направил Лейбницу ответ, в котором указывается разложение в ряд для синуса и арксинуса, полученное Ньютоном, ряды Грегори для тангенса и арктангенса, а также некоторые результаты, касающиеся интерполяции, квадратур и других задач. Как бы то ни было, в письме приводились лишь результаты, но не объяснялось, каким способом они были получены. Лейбниц приписал авторство этих рядов Ольденбургу и, по мнению Хоффмана, не совсем понял, что попало ему в руки, так как пообещал сравнить эти результаты со своими и дать по этому поводу комментарий, но так никогда и не сделал этого. Так как о некоторых из этих рядов Лейбниц узнал позднее и из других источников, это дало Ньютону основания впоследствии обвинить его в плагиате результатов, полученных через Ольденбурга.
Мы можем достаточно точно указать, когда Лейбниц открыл анализ бесконечно малых. Это произошло в конце октября — начале ноября 1675 года, если вообще уместно приводить столь точные даты для такого значимого открытия. В сохранившихся рукописях, которые относятся к этому периоду, особенно тех, что датированы 29 октября и 11 ноября, Лейбниц вводит систему обозначений математического анализа и описывает с ее помощью алгоритм, в котором впоследствии станут заметны различия с работами его предшественников, приводит правила анализа и определяет интегрирование и дифференцирование как взаимно обратные операции. Хоффман пишет: «После того как был сделан этот первый, решающий шаг в сторону «алгебраизации» задач о бесконечно малых, перед этим человеком, умевшим определить характерные и общие элементы среди мешанины похожего, открылась новая картина мира. <…> Он четко понимал, чего не хватает в созданном им математическом анализе, но знал, что эти недостатки можно исправить и что путь в новый мир успешно открыт».
Ключевую роль сыграли работы по решению задач поиска кривой по заданной касательной, которыми Лейбниц занимался в октябре 1675 года. За год до этого он решил задачу определения кривой по известной поднормали.
В рукописи, датируемой 29 октября 1675 года, Лейбниц ввел знак ∫ — стилизованную букву S, первую букву латинского слова summa для обозначения суммы бесконечно малых. До этого использовалась аббревиатура omn. — от латинского de omnium («все»), введенная Кавальери. Лейбниц писал: «Будет удобно записывать omn. как ∫, так что ∫l = omn.l, то есть сумма l».
Далее в этой же рукописи он вводит букву d для обозначения дифференциала.
Изначально он поместил это обозначение в знаменатель: «Это получается обратным расчетом. То есть допустим, что ∫l = уа, где l = ya/d. Тогда с ростом ∫d будет уменьшаться в размерах. Однако ∫ означает сумму, a d — разность».
Спустя несколько дней в рукописи, датированной 11 ноября 1675 года, он переместил d в числитель и записал — как dx. В этой же рукописи Лейбниц задается вопросом о равенстве d(xy) и dxdy, а также
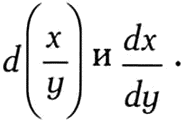 Он делает вывод, что равенство между ними не выполняется, однако не приводит верных формул для нахождения дифференциала произведения и частного.
Чтобы увидеть нечто общее среди беспорядочного множества результатов, полученных его предшественниками при решении задач о квадратурах, центрах тяжести, касательных, задач нахождения кривой по заданной касательной и других, и сформулировать понятия интегрирования и дифференцирования, требовался алгебраический язык. Этот язык Лейбниц в совершенстве освоил во время работы над решением уравнений, проведенной за несколько месяцев вплоть до октября 1675 года. Следует отметить, что Лейбниц не преуспел в решении уравнений, однако освоил язык алгебры, без которого не смог бы впоследствии открыть свой метод математического анализа.
Он делает вывод, что равенство между ними не выполняется, однако не приводит верных формул для нахождения дифференциала произведения и частного.
Чтобы увидеть нечто общее среди беспорядочного множества результатов, полученных его предшественниками при решении задач о квадратурах, центрах тяжести, касательных, задач нахождения кривой по заданной касательной и других, и сформулировать понятия интегрирования и дифференцирования, требовался алгебраический язык. Этот язык Лейбниц в совершенстве освоил во время работы над решением уравнений, проведенной за несколько месяцев вплоть до октября 1675 года. Следует отметить, что Лейбниц не преуспел в решении уравнений, однако освоил язык алгебры, без которого не смог бы впоследствии открыть свой метод математического анализа.

Дом, в котором жил Лейбниц во время пребывания в Ганновере.
Лейбниц сообщил основу своего метода Ньютону в ответ на его письма, переданные через Ольденбурга в июне и октябре 1676 года. Эта переписка Ньютона и Лейбница впоследствии сыграла решающую роль в споре о том, кто же первым создал анализ бесконечно малых. Как мы уже говорили, Ньютон отправил Лейбницу два письма: так называемое Epistolae prior, датированное 13 июня 1676 года, и Espistolae posterior, датированное 24 октября 1676 года. Ответы Лейбница датируются 17 августа 1676 года и 11—12 июня 1677 года. Они не озаглавлены, но их значение не менее масштабно. В своих письмах Ньютон излагает Лейбницу большую часть De analysi и De methodis о разложении в ряд, но почти не упоминает о своей версии анализа бесконечно малых. Лейбниц же в своих письмах излагает свой метод полностью. Ньютону следовало понять, что метод Лейбница столь же полон, как и его собственный, и вовремя опубликовать свои труды, чтобы доказать свое первенство. Вестфолл пишет: «Можно лишь предполагать, каковы были бы возможные последствия этого шага, но можно с уверенностью сказать, что в этом случае обе стороны не запятнали бы себя позорными поступками, которые в итоге совершили». Валлис чрезвычайно проницательно заметил: «По моему мнению, господину Ньютону следует усовершенствовать свою нотацию и незамедлительно опубликовать эти письма [имеются в виду два Epistolae]». Годы, проведенные в Париже, стали для Лейбница непростыми. После смерти курфюрста Майнца в феврале 1673 года и изменений в ходе военных действий между Францией и Голландией политическая и дипломатическая миссия Лейбница потеряла смысл. Лейбниц опасался, что ему прикажут вернуться в Германию. Однако его новый покровитель предложил ему остаться в Париже и продолжать работу. Лейбниц предпринял несколько неудачных попыток получить должность во французской столице. Ему не удалось получить пост дипломата (этому помешало его происхождение), а также не удалось занять оплачиваемый пост во Французской академии наук, где он представил свою вычислительную машину в начале 1675 года. (К сожалению для него, оплачиваемые должности уже занимали Гюйгенс и Кассини, и Академия не могла принять еще одного иностранца.) Несмотря на то что Лейбниц в течение всей второй половины того года использовал все свои многочисленные связи, попытка получить должность заведующего кафедрой в Коллеж де Франс после смерти Роберваля также окончилась неудачей. Шло время, но единственное предложение, которое ему поступило, — это приглашение на службу к графу Иоганну Фридриху, курфюрсту Ганновера. Лейбниц в конце концов принял предложение, но это означало, что ему придется вернуться в Ганновер, жить вдали от главных научных центров того времени и полностью зависеть от курфюрста, рискуя потерять должность в любой момент. Ему удалось продлить свое пребывание в Париже, насколько это было возможно — сначала до мая 1676 года, затем до октября. 4 октября он оставил Париж и направился в Германию, где его ждала должность библиотекаря в Ганновере. К работе следовало приступить в январе. Он больше никогда не возвращался в город, где в условиях величайшего давления, обеспокоенный будущей карьерой, он открыл анализ бесконечно малых. По пути в Ганновер Лейбниц посетил Лондон и Амстердам. В Лондоне он пробыл десять дней и нанес визит Коллинзу. Вестфолл пишет: «Находясь под впечатлением от визитера, Коллинз открыл перед ним свой архив». Лейбниц, помимо прочих трудов, ознакомился с «Анализом» Ньютона и сделал некоторые пометки, касавшиеся разложения в ряд. Вновь приведем цитату Вестфолла: «Он увидел, что в этой области он может многому научиться у британских математиков. Отсутствие пометок, касающихся анализа флюксий, означает, что он не увидел в книге Ньютона ничего такого, о чем не знал бы сам. После отъезда Лейбница Коллинз вернулся к реальности и осознал, насколько опрометчиво поступил. Он никогда не рассказывал Ньютону о том, что показал Лейбницу его труды… Лейбниц, в свою очередь, также предпочел не упоминать об этом». Позднее Лейбниц предпочел умолчать не только об этом, но и о других вещах, которые он узнал по дороге в Германию. В Амстердаме он в течение месяца несколько раз встретился с философом Бенедиктом Спинозой и ознакомился с частью рукописи его «Этики». Позднее Лейбниц отрицал идеи Спинозы (на момент визита Спинозе, которому оставался всего год до смерти, наскучило всякое общество) и предпочел не упоминать о том, как много он узнал во время бесед с ним, и также отказывался признавать значительное влияние «Этики» на свои философские взгляды. Когда 25 лет спустя начался спор о том, кто же первым открыл математический анализ, решающую роль сыграло то, что Лейбниц увидел в Лондоне.
Портрет Бенедикта Спинозы. Доктрина этого философа, жившего в изгнании, оказала огромное влияние на многих философов, среди которых был и Лейбниц.
В 1677 году, уже будучи в Ганновере, Лейбниц получил правильные формулы для вычисления дифференциала произведений, дробей и степеней. Эти формулы он вывел не без труда, путем проб и ошибок. В 1680 году он практически завершил работу над своим методом анализа и, в отличие от Ньютона, который не горел желанием отдавать рукописи в печать, опубликовал первую статью по этой теме в 1684 году. Эта статья стала первой в истории публикацией, посвященной анализу бесконечно малых. Она имела внушительное заглавие «Новый метод максимумов и минимумов, а также касательных, для которого не являются препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления». В этой статье объемом всего в шесть страниц крайне схематично, без доказательств и практически без примеров было изложено дифференциальное исчисление Лейбница. Эта работа была сложной и непонятной, «скорее, загадка, нежели объяснение», как отзывались о ней братья Бернулли, которые первыми изучили математический анализ Лейбница. Сложность статьи усугублялась опечатками, допущенными при публикации. Особого упоминания заслуживает один из немногих примеров, приведенных в статье, которому Лейбниц посвятил заключительные строки. Речь идет о задаче нахождения кривой по известной касательной, предложенной де Боном: «Я с удовольствием приведу в качестве приложения решение задачи, предложенной де Боном, которую безуспешно пытался решить Декарт. Найти линию такой природы, что проекция любой из ее точек на ось и точка пересечения касательной в этой точке с указанной осью образуют отрезок постоянной длины». Чтобы найти решение с помощью своего метода и тем самым доказать его возможности, Лейбницу понадобилось всего полдюжины строк. Искомой кривой в этой задаче является логарифмическая кривая. Также следует обратить внимание, насколько своеобразным способом Лейбниц распространял информацию о своем дифференциальном исчислении. Он опубликовал свою работу в научном журнале Acta eruditorum, в создании которого участвовал в 1682 году, ознаменовав тем самым начало новой эпохи в науке.ПРОБЕЛЫ В РАССУЖДЕНИЯХ ГЕНИЯ
Приведем вывод формулы производной произведения функций, изложенный Лейбницем, так как в нем ярко отражена недостаточная логическая строгость, которой отличался Лейбниц при работе с бесконечно малыми величинами: «d(xy) — то же, что и разность между двумя смежными xy, из которых одним будет xy, другим — (x + dx) (у + dy). Следовательно, d(xy) — (x + dx) (у + dy) — xy, или xdy + ydx + dxdy, что равно xdy + ydx, если опустить величину dxdy, которая является бесконечно малой по отношению к прочим величинам, так как dx и dy предполагаются бесконечно малыми». Как видите, четкость этого доказательства оставляет желать лучшего. В нем проявляется наиболее противоречивое свойство бесконечно малых величин: Лейбниц считает величину dxdy равной нулю, несмотря на то что ни dx, ни dy не равны нулю.
Спустя два года, в 1686 году, Лейбниц публикует в Acta eruditorum свою вторую статью, которая на этот раз посвящена интегральному исчислению. Статья носила название «О скрытой геометрии и анализе неделимых и бесконечных величин». Лейбниц начал эту статью с оправданий, объясняя, почему его первая статья была столь сложной: «Понимая, что некоторые вещи, опубликованные мной в Acta об открытиях в геометрии, не были в достаточной мере поняты некоторыми учеными людьми и, более того, использованы не совсем верно, будь то по ошибке либо по какой-либо другой причине, я посчитал, что крайне ценно добавить к этой статье все возможное, чтобы прояснить прошлые вопросы». В этой статье впервые используется обозначение интеграла, хотя из-за сложностей при печати знак ∫, примененный Лейбницем в рукописи, был заменен на f, что было исправлено в последующих изданиях. В статье, как и в первой от 1684 года, используется буква d для обозначения дифференциала. Во второй статье он указывает, что дифференцирование и интегрирование являются взаимно обратными операциями, и формулирует основную теорему анализа: «Подобно степеням и корням в обычном исчислении, а также сумме и разности, J и d являются обратными». Он применяет это утверждение для доказательства теоремы, которую приписывает Барроу, для чего, как и при решении задачи де Бона, которой оканчивается первая статья, он решает дифференциальное уравнение. «Из изложенного в методе касательных очевидно, что
 Следовательно, обратной является
Следовательно, обратной является
1/2∙x2 = ∫xdx».
Происхождение названия объясняется использованием латинского слова differentia — «разность». Отсюда понятие дифференциала и название «дифференциальное исчисление». Последовав совету Иоганна Бернулли, Лейбниц заменил изначальное название «суммарное исчисление» на «интегральное исчисление». Иоганн Бернулли также предлагал заменить символ ∫ буквой I — первой буквой слова «интеграл». В итоге они договорились сохранить название «интегральное исчисление», предложенное Бернулли, и символ ∫, предложенный Лейбницем. В письме, датированном 28 февраля 1695 года, Лейбниц пишет Иоганну Бернулли: «В будущем было бы лучше с целью единообразия и гармонии не только между нами, но и во всей области изучения использовать термины сумм вместо твоих интегралов. Тогда, например, ∫ydx будет означать сумму всех y, умноженных на соответствующий dx, или сумму всех этих прямоугольников. Я прошу этого главным образом потому, что в этой форме геометрические суммы, или квадратуры, лучше соответствуют арифметическим суммам и суммам рядов. Признаюсь, что открыл весь метод, рассматривая обоюдность сложения и вычитания, а затем в своих рассуждениях перейдя от последовательностей чисел к последовательностям отрезков и ординат». Лейбниц опубликовал и другие статьи на тему анализа бесконечно малых. Профессор Норберто Куэста Дутари насчитал 27 статей, напечатанных в период с 1684 по 1708 год только в выпусках журнала Acta eruditorum. Первооткрыватели анализа различались и в этом: Лейбниц предпочитал публиковать статьи в научных журналах, чтобы быстрее познакомить общественность с полученными результатами, а Ньютон издавал их в виде книг и постоянно откладывал публикацию.На службе у Ганноверской династии
Когда Лейбниц вернулся в Германию, он некоторое время оставался без работы, так как фон Бойнебург умер в конце 1672 года, а несколько месяцев спустя скончался сам курфюрст. Он не смог найти ничего лучше, чем должность библиотекаря на службе курфюрста Ганновера. К сожалению для него, должность требовала, чтобы он непрерывно находился в столице Нижней Саксонии, вдали от Парижа, который в те годы был центром европейской науки, культуры и философии. Ганноверский герцог Брауншвейг-Люнебургский стал его покровителем до конца жизни, однако жизнь в доме герцога не всегда была ему по нраву. В 1678 году он стал личным советником герцога, а в 1685 году занялся изучением истории его семейства. Однако его обязанности на этом не заканчивались. С Лейбницем советовались по вопросам образования; также он занимался инженерным делом и геологией в шахтах, расположенных в горах Гарца, где спроектировал систему дренажа шахт с помощью ветряных мельниц. Затея с мельницами завершилась неудачей и ударила по карману Лейбница, так как ему пришлось оплатить расходы из своего жалования. Часть средств, которые планировалось получить от системы дренажа, должна была пойти на создание академии и развитие characteristica universalis, но этот проект так никогда не был осуществлен. Лейбниц также занимался созданием гидравлических прессов, часов и других устройств. Не будем забывать и о спроектированной им вычислительной машине. Возможно, наибольших успехов на службе у герцога Брауншвейгского он добился как историк. Лейбниц без устали исследовал старые рукописи из баварских монастырей и итальянских палаццо, эпитафии на заброшенных могилах неизвестных кладбищ кармелитов и в итоге установил родство семьи герцога и древнего княжеского рода Эсте из Модены. Благодаря этим исследованиям герцог Брауншвейгский впоследствии добился того, что его княжество стало новым, девятым курфюршеством Германии, и герцог получил право голоса при избранииимператора. Лейбниц как историк достиг удивительных высот, так как описал не только историю рода герцога, но и попытался составить всеобщую историю Земли, охватывавшую также геологию и археологию, а также провести исследование миграции народов на основе различий и аналогий между языками. Подобно другим грандиозным проектам, этот труд по всеобщей истории так никогда и не был создан, и все идеи ученого растворились в море рукописей и писем. И снова обратим внимание, сколь велики различия между Ньютоном и Лейбницем даже в том, в каких условиях им приходилось работать. Ньютон в одиночестве изучал труды о жизни библейских царей, стремясь глубже понять творение Бога Отца. Жил он сначала в Кембридже, подобно монаху, затем в Лондоне, наслаждаясь высоким положением и властью. Лейбниц же, напротив, посетил множество архивов и библиотек, в течение трех лет путешествовал по югу Германии, Австрии и Италии, не считая коротких поездок в Берлин, Ганновер, Вольфенбюттель и Вену, разыскивая предков своего покровителя. При этом герцог весьма щепетильно следил за его работой, и если замечал, что его генеалогическое дерево не растет, как бы того ему хотелось, то объяснял это недостатком усердия своего подчиненного.
С восшествием на трон короля Англии Георга I отношение к труду Лейбница заметно ухудшилось. Вверху — портрет короля кисти Готфрида Кнеллера.
ОЧАРОВАНИЕ ВОСТОКОМ
Увлечение Лейбница Китаем никого не удивило бы в наши дни, но в то время оно считалось необычным. В этом увлечении проявилось стремление Лейбница знать всё. Его очень заинтересовала система китайского письма: он увидел в ней сходство со своим «универсальным языком». Его увлеченность была столь велика, что он советовал отправить в Китай протестантских миссионеров и отметил, что если китайский император примет протестантскую веру, это будет важнее победы в сотне сражений. В то время на императора имели влияние монахи-иезуиты, которые, в частности, обучали его и некоторых членов его семьи математике и астрономии.

Страница статьи «Изложение двоичной арифметики» (1703-1705), на которой изображены гексаграммы из Книги Перемен.
Лейбниц считал, что смог расшифровать значение этих древних символов с помощью созданной им двоичной системы счисления.
Отношения Лейбница с семьей герцога ухудшились после смерти Эрнста Августа в 1698 году, на смену которому пришел его сын и наследник Георг Людвиг. Будущий король Англии Георг I никогда не ладил с Лейбницем, несмотря на то что тот находился в прекрасных отношениях с матерью курфюрста герцогиней Софией и его сестрой Софией Шарлоттой. Курфюрст не ценил интеллект Лейбница и вспоминал об ученом лишь тогда, когда исследования истории его рода, по его мнению, продвигались недостаточно быстро. Добавим к этому, что Лейбниц старался под любым предлогом уехать из Ганновера: он посещал заседания Академии наук в Берлине, наносил визиты императору Священной Римской империи в Вене (в январе 1712 года ему была пожалована должность придворного советника) и российскому царю Петру I. Лейбниц был советником Петра с 1711 года и весьма способствовал развитию в России математики и других наук, а также содействовал реформе права и государственного устройства. Он также посещал многочисленных принцев, принцесс и курфюрстов Германии, состоявшей тогда из множества княжеств, герцогств и городов-государств. Хотя Георг Людвиг Брауншвейгский не ценил бриллиант, сверкавший в его доме, он чувствовал зависть соседей и непрестанно упрекал Лейбница в том, что тот под любым предлогом оставлял исследования родословной герцога и занимался своими многочисленными проектами, начиная от написания философских трудов и заканчивая расшифровками китайской Книги Перемен. Благодаря вежливости и умению произвести хорошее впечатление Лейбниц поддерживал дружеские отношения со многими людьми по всей Европе. Разумеется, у него были недоброжелатели, он участвовал в спорах и порой действовал не совсем благоразумно, но он не обладал столь сложным характером, как Ньютон.Философия Лейбница
Философские взгляды Лейбница изложены в его немногочисленных трудах. Возможно, их было бы больше, если бы обстоятельства складывались благоприятнее. Заслуживают упоминания «Размышления о познании, истине и идеях» — небольшая статья, опубликованная в Acta eruditorum в 1684 году, а также «Рассуждение о метафизике» (1686), «Опыты теодицеи о благости Божией, свободе человека и начале зла» (1710) и «Монадология» (1714). Однако большинство его трудов по метафизике и философии (лучшие, по мнению Бертрана Рассела) не были изданы в виде книг, а зафиксированы лишь в его обширной переписке. В основе его философии лежит сложная совокупность различных принципов. Часть из них относится к реальности: принципы предустановленной гармонии, полноты, непрерывности, тождества, известный также как закон Лейбница. Другие относятся к способу понимания реальности: принцип непротиворечивости или принцип достаточного основания. Этот список можно продолжать и далее. Автор этой книги не ставил перед собой задачу погрузиться в глубины философской мысли Лейбница, однако было бы непростительно не упомянуть о ней вовсе. Его система философских взглядов чрезвычайно разнообразна и обширна, однако ей присущи единообразие и по меньшей мере непротиворечивость. Рассмотрим принцип непрерывности. Может показаться странным, что его придерживался создатель монады — «простой субстанции, являющейся частью сложных; простой в том смысле, что она не содержит частей», и ученый, по мнению которого продолжение прямой состояло из несокращаемых частей бесконечно малой длины. Да, подобная несогласованность может показаться странной и противоречивой, однако именно принцип непрерывности позволил Лейбницу перейти от последовательностей чисел к последовательностям бесконечно малых, образующих непрерывное целое, что аналогично переходу от разности чисел к дифференциалу. Хосе Ферратер Мора писал: «Принцип непрерывности — это всеобщий принцип, который делает очевидной согласованность физики и геометрии. Согласно этому принципу, всё во Вселенной связано “на основании метафизических причин”, причем не только в настоящем, но и с течением времени, поскольку настоящее всегда таит в себе ключ к будущему. Благодаря принципу непрерывности можно дать обоснование любой реальности и любому событию, поскольку без этого принципа следовало бы сделать вывод, что в природе существуют промежутки, что не согласуется с принципом достаточного основания». Принцип достаточного основания, в свою очередь, гласит, что «ни одно явление не может оказаться истинным или действительным, ни одно утверждение — справедливым без достаточного основания, почему именно дело обстоит так, а не иначе». Здесь основание понимается как повод, а не как логическая необходимость. Принцип достаточного основания позволил распутать клубок причин и прийти к первопричине и источнику предустановленной гармонии — к Богу. (Лейбниц имел склонность к поиску более или менее логичных доказательств существования Бога.) Согласованность и универсальность философских взглядов Лейбница снова обнаруживается в применении принципа непрерывности к переселению народов. Лейбниц рассуждал так: если мы признаем, что человеческий язык развивается непрерывно, то любое отсутствие непрерывности будет соответствовать очередному этапу миграции населения.ЛЕЙБНИЦ И БРАК
В вопросах любви, как и во многих других, Лейбниц не отличался столь пуританским характером, как Ньютон. Известно, что в возрасте 50 лет он подумывал о браке, но его избранница размышляла дольше положенного времени, и Лейбниц утратил интерес к супружеству. Эту историю рассказывал Фонтенель, хотя впервые о ней поведал Экхарт — секретарь и первый биограф Лейбница. Позднее многие математики при случае в шутливой форме вспоминали об этой истории. Например, Лагранж писал Д’Аламберу: «Не знаю, верно ли я провел расчеты или нет, скорее, я не рассчитывал ничего, иначе уподобился бы Лейбницу, который размышлял об этом слишком много и никак не мог решиться. Как бы то ни было, признаюсь вам, что никогда не испытывал желания жениться и никогда не сделал бы этого, если бы меня не заставили обстоятельства».
Похороны Лейбница
Похороны Лейбница, умершего 14 ноября 1716 года, также отличались от похорон Ньютона. Возможно, это было вызвано непростыми отношениями Лейбница с Георгом Брауншвейгским, которые ухудшились после смерти в 1705 году его сестры Софии Шарлотты, тогдашней королевы Пруссии, и после смерти матери герцога в 1714 году. Лейбниц возвратился в Ганновер в середине того же года, проведя более полутора лет в Вене, когда Георг унаследовал британский престол. Лейбниц хотел последовать за своим покровителем в Англию — именно в тот период спор с Ньютоном о первенстве был как никогда ожесточенным. Поэтому Лейбницу хотелось находиться в стране, где его считали врагом, будучи членом королевского двора (чего опасались сторонники Ньютона), и он несколько раз пытался получить в Англии должность историографа. Хотя Лейбниц в 1700 году блестяще провел дело о праве герцога Брауншвейгского на английский престол, Георг I не хотел, чтобы его придворный историк отвлекался на споры об анализе бесконечно малых, оставив без внимания составление королевской родословной. Поэтому он повелел Лейбницу остаться в Ганновере, что было для него равносильно изгнанию, и практически заключил его под домашний арест, запретив ему в 1715 году длительные поездки и лишив жалования за два с половиной года, поскольку Лейбниц слишком долго находился в Вене. Король был непреклонен: он повелел Лейбницу завершить родословную его династии, носившую название Anuales Imperti Occidentis Brunsvicensis. Этот труд так и не был доведен до конца и, как признавался Лейбниц, был для него сродни сизифовому труду. Лейбниц был похоронен без почестей, под песнопения, исполненные детским хором, в кругу ближайших родственников и друзей. На похоронах не появился ни один из членов королевского двора, хотя в те самые дни король со своей свитой были на охоте в соседнем поместье. Больше полувека его могила простояла без надписи. Об этом не позаботился ни единственный племянник ученого, который получил от него в наследство хорошее состояние, ни Брауншвейгская династия, которой он верой и правдой служил много лет.Глава 5. Спор о первенстве
В этой главе мы расскажем о долгом и неприятном споре между Ньютоном и Лейбницем, а также их сторонниками о том, кто же первым открыл анализ бесконечно малых. Следует вкратце рассказать, чем отличались варианты математического анализа, предложенные Лейбницем и Ньютоном. Так мы лучше сможем оценить, насколько концептуальными были различия между ними. Начиная с 1666 года Ньютон рассматривал кривые (флюенты) как результат движения точки. Тогда же он сформулировал понятие флюксии — производной по времени. Отметим, что флюксия флюента в данный момент времени (иными словами, мгновенная скорость) — это число. Он разработал алгоритмы вычисления флюксий, эквивалентные современным правилам нахождения производной для сумм, разностей, произведений и дробей, а также показал, что для расчета площади области, ограниченной кривой, достаточно вычислить флюент флюксии. Говоря современным языком, это означает, что нужно найти первообразную функции и применить основную теорему анализа. Именно здесь используются степенные ряды: в соответствии с нынешней терминологией, для расчета флюента флюксии последняя раскладывается в степенной ряд, после чего выполняется почленное интегрирование по правилу нахождения интеграла степенной функции. Лейбниц, напротив, рассматривал кривые как ломаные линии из прямых отрезков бесконечно малой длины, а касательные — как продолжения этих отрезков. Он полагал, что геометрия кривой, описанная формулой, которой задается кривая, определяет дифференциалы аргумента и функции. Он также «определил» понятия дифференциала и интеграла, точнее говоря, описал их особенности, в отличие от Ньютона, который рассматривал дифференциал функции как бесконечно малую величину. Он доказал, что дифференцирование и интегрирование являются взаимно обратными операциями, то есть доказал основную теорему анализа и описал процесс вычисления дифференциалов (сформулировал правила вычисления производных), а также вычислил производные элементарных функций. Производные элементарных функций Лейбниц описал в намного более символическом виде, чем Ньютон: Лейбниц отдавал предпочтение свернутым выражениям, а не разложениям в ряд. Важной особенностью методов Лейбница является то, что он всегда разделял открытие разложения в степенной ряд и открытие анализа бесконечно малых. Открытие разложения в степенной ряд он неизменно приписывал Ньютону, в то время как вокруг анализа бесконечно малых развернулась нешуточная борьба. Лейбниц считал, что первенство принадлежит ему, и полагал, что Ньютон совершил свое открытие, используя письма Лейбница, написанные им в ответ на Epistolae prior и Epistolae posterior. Ньютон же настаивал на том, что оба открытия неразделимы, и утверждал, что Лейбниц, узнав от него о способе разложения в ряд, был обязан ему открытием дифференциального исчисления.Взаимное признание заслуг, пусть и не вполне искреннее
Хотя Ньютон первым открыл и описал свой вариант математического анализа, на 10 лет опередив Лейбница, последний опубликовал свои результаты раньше. В первой своей статье, опубликованной в 1684 году, Лейбниц не упоминает Ньютона, но говорит о нем во второй статье (1686 год): «Дабы не казалось, что я приписываю себе излишне много либо недооцениваю остальных, следует упомянуть в нескольких словах о том, что моей формуле я особенно обязан прославленным математикам нашего века в жанре геометрии. <…> Кроме того, светлейший математик Николас Меркатор из Гольштейна был первым, насколько мне известно, кто нашел квадратуру с помощью бесконечного ряда. Независимо от него это открытие совершил, а также улучшил его геометр величайшего дарования Исаак Ньютон, который, если бы дал нам ознакомиться с его мыслями, которые, насколько я понимаю, он имеет, то открыл бы нам новые пути к удивительным открытиям и научным трудам». Ньютон упомянул Лейбница при первой же возможности. Эта возможность представилась ему в 1687 году, при публикации первого издания «Начал». Как известно, в «Началах» Ньютон предпочел использовать язык геометрии, подобно древним грекам. В кульминационные моменты спора он часто указывал, что использовал анализ флюксий для вывода значительной доли результатов, изложенных в «Началах», однако затем изложил их на языке геометрии. Возможно, дело и правда обстояло так, как указывает Ньютон, но этому нет документальных подтверждений. Как неоднократно указывает Уайтсайд, рукописи, где, по словам Ньютона, с помощью анализа флюксий выводятся результаты, изложенные в «Началах», так и не были найдены. Тем не менее Вестфолл пишет: «Проблема, связанная с «Началами», заключается не в том, чтобы найти доказательства, полученные другим способом, а в том, чтобы обнаружить признаки математического анализа, скрытые за завесой геометрии». Анализ флюксий Ньютона вообще не упоминается в «Началах», за исключением леммы II книги II, что мы уже указывали в главе 3. В этой лемме Ньютон вкратце излагает современные правила вычисления производной. Он приводит примечание к этой лемме, где цитирует Лейбница и явно заявляет права на создание математического анализа. Так Ньютон отреагировал на первую публикацию Лейбница, посвященную анализу бесконечно малых. Это примечание звучит следующим образом: «В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком Г.Г. Лейбницем, я ему сообщал, что я обладаю методою для определения максимумов и минимумов, проведения касательных и решения тому подобных вопросов, одинаково приложимою как для членов рациональных, так и для иррациональных, причем я ее скрыл, переставив буквы следующего предложения: «Data aequatione quotcunque fluentes quantitae involvente fluxiones invenire et vice versa» («Когда задано уравнение, содержащее любое число переменных количеств, найти флюксии, и наоборот»). Знаменитейший муж отвечал мне, что он также напал на такую методу, и сообщил мне свою методу, которая оказалась едва отличающейся от моей, и то только терминами и начертанием формул. Основа обоих метод содержится в этой лемме». Ньютон написал это примечание с целью заявить право первенства на открытие анализа, однако так как ранее он не публиковал ничего по этому вопросу, в отличие от Лейбница, а письма, которыми обменивались Ньютон и Лейбниц, были известны лишь узкому кругу его друзей, примечание было понято как знак того, что Ньютон признает за Лейбницем право первенства.
Французское издание «Метода флюксий», датированное 1740 годом.
В конце 1691 года, спустя четыре года после выхода «Начал», в кругах, близких к Ньютону и Лейбницу, стали циркулировать слухи о том, чему именно Лейбниц научился у Ньютона. Так, Фатио де Дюилье писал Гюйгенсу: «Господин Ньютон, несомненно, является первооткрывателем дифференциального исчисления, так как оно было ему известно еще до того, как господин Лейбниц получил о нем первое представление. Более того, это представление он мог получить лишь после того, как увидел записи господина Ньютона. Поэтому я крайне удивлен тем, что господин Лейбниц не упоминает об этом в журнале Acta». Фатио вернулся к этой теме 5 февраля 1692 года: «Не сомневаюсь, что публикация писем [Epistolae prior и Epistolae posterior] повлечет за собой унижение для господина Лейбница, так как он опубликовал свои правила дифференциального исчисления лишь по прошествии достаточного времени после их получения и сделал это без упоминания о господине Ньютоне. Они были представлены в виде переделки того, что получил господин Ньютон, и если мы сравним их, то не сможем отделаться от мысли, что разница между ними такова же, как между совершенным оригиналом и грубой и несовершенной копией». Учитывая написанное Фатио, можно считать, что именно он положил начало спору, хотя весьма вероятно, что он написал Гюйгенсу то, что в это же время говорили Ньютону другие.ПЕРВЫЕ ИЗВИНЕНИЯ
В 1693 году Ньютон и Лейбниц вновь обменялись письмами. Лейбниц написал Ньютону в марте (это, возможно, было вызвано известием о том, что Ньютон собирается опубликовать рукопись, о чем Лейбницу сообщил Гюйгенс). Ответ Ньютона последовал в октябре. Эта переписка была краткой и с научной точки зрения не идет ни в какое сравнение с письмами от 1676 года. Отметим несколько фрагментов из письма Ньютона. С одной стороны, оно начинается с теплого приветствия: «Я не ответил вам сразу по получении вашего письма, поскольку оно выскользнуло у меня из рук, затерялось среди прочих бумаг, и до вчерашнего дня я не мог отыскать его. Это огорчило меня, поскольку я очень ценю вашу дружбу и уже много лет считаю вас одним из первых геометров столетия, что признавал всякий раз, когда мне предоставлялась на то возможность». Первый абзац завершается благородным признанием, которое по прошествии лет полностью обесценилось и утратило смысл: «Ожидаю, что не написал ничего такого, что могло бы прийтись вам не по нраву, и если, по вашему мнению, что-то заслуживает цензуры, пожалуйста, без колебаний сообщите мне об этом в письме, так как я больше ценю своих друзей, чем математические открытия».
Пять лет спустя мы услышим аналогичные упреки в адрес Ньютона. В письме, датированном 15 августа 1696 года, Иоганн Бернулли писал Лейбницу: «Не знаю, изобрел ли Ньютон свой метод после того, как увидел ваше исчисление, особенно когда вижу, чем вы поделились с ним до того, как он опубликовал свой метод». В этом письме впервые допускается возможность того, что Ньютон заимствовал результаты Лейбница.
«Скромность есть добродетель, но излишняя робость есть недостаток»
С 1691 года Ньютону все чаще советовали опубликовать свои работы. Наиболее настойчивым был Джон Валлис; он особенно настаивал на публикации Epistolae prior и Epistolae posterior. В 1695 году он известил Ньютона о том, какое признание получил Лейбниц за открытие своего метода исчисления: «От ваших друзей из Голландии мне стало известно, что ваши флюксии были встречены там с великим одобрением под наименованием дифференциального исчисления Лейбница. <…> Вы недостаточно заботитесь о своей репутации и о репутации страны, если позволяете, чтобы подобные ценности находились рядом с вами неподвижно, пока кто-то другой не снискает славу, которая должна принадлежать вам. Я позаботился о том, чтобы добиться справедливости по этому вопросу, и теперь жалею, что не опубликовал эти два письма слово в слово». Валлис продолжал настаивать: «Скромность есть добродетель, но излишняя робость, особенно в наше время, есть недостаток». Два года спустя Валлис сообщил Ньютону, что собирается опубликовать Epistolae prior и Epistolae posterior, если только не получит явного на то запрета от Ньютона. В итоге письма были опубликованы в полном объеме в 1699 году в одном из томов собрания сочинений Валлиса по математике. В него также были включены копии ответных писем Лейбница. Валлис получил разрешение Лейбница на публикацию этих писем заранее и потратил на это намного меньше усилий, чем на получение разрешения от Ньютона.
Из писем Ньютона и Лейбница, опубликованных Джоном Валлисом, стало очевидно, что Ньютон первым открыл свой метод исчисления.
Эта публикация изменила положение дел в споре за первенство: Валлис, пусть и не совсем точно, продемонстрировал, какими результатами располагали Ньютон и Лейбниц в 1676 году. Важнее всего было то, что впервые были преданы гласности документы, доказывающие, что Лейбниц опубликовал свою версию раньше, но Ньютон совершил открытие первым, сообщив об этом, пусть и неявно, Лейбницу по его просьбе. Летом 1699 года Лейбниц пишет: «Валлис попросил у меня разрешения на публикацию моих старых писем. <… > Поскольку мне нечего опасаться… я подтвердил, что он может публиковать все, что посчитает нужным». Очень скоро оказалось, что Лейбниц напрасно считал, что ему «нечего опасаться».«По когтям узнают льва»
В тот же период произошел инцидент, который в высшей степени способствовал обострению дискуссии. Речь идет о знаменитой задаче о брахистохроне, предложенной Иоганном Бернулли в июне 1696 года. В ней требовалось найти кривую, двигаясь по которой исключительно под действием силы тяжести, тело пройдет путь из точки A в точку B за наименьшее время. В мае 1697 года Лейбниц опубликовал присланные ему решения задачи. Всего было получено четыре решения, авторами которых были сам Лейбниц, маркиз Лопиталь, Якоб Бернулли и автор задачи, Иоганн Бернулли. Также было прислано решение неизвестного автора, которое было впервые опубликовано в январе 1967 года в журнале «Философские записки». Как мы знаем, этим неизвестным автором был Ньютон. Увидев простое решение этой задачи, содержавшее всего 77 слов, Иоганн Бернулли угадал автора. Он сказал: «Tanquam ex ungue leonem» — «По когтям узнают льва». Во всех решениях, за исключением предложенного Лопиталем, искомой кривой являлась циклоида. Продолжение истории, о котором мы расскажем далее, зафиксировано в воспоминаниях племянницы Ньютона и в переписке Иоганна Бернулли и Лейбница. Возможно, целью задачи, предложенной Иоганном Бернулли, было подтвердить возможности ньютоновского анализа бесконечно малых. В письме Иоганну Бернулли, датированном февралем 1697 года, Лейбниц писал, что только он сам, братья Бернулли, маркиз Лопиталь и Ньютон были способны решить эту задачу, так как в то время только им был известен анализ бесконечно малых, необходимый для ее решения. Именно по этой причине, как объяснял Лейбниц, эту задачу в свое время не смог решить Галилей: ему был неизвестен математический анализ. Таким образом, неизвестным автором решения был не кто иной, как Ньютон, который в то время занимал должность смотрителя Монетного двора и не отошел от научной деятельности. Ньютон получил письмо с задаче о брахистохроне 29 января 1697 года. По рассказам его племянницы, письмо попало в руки Ньютона в четыре часа дня, когда тот усталый вернулся из Монетного двора — в то время полным ходом шла чеканка монет нового образца. Спустя 12 часов, то есть в четыре часа утра, решение было готово. Племянница Ньютона не знала, что он вполне мог отыскать решение в глубине своей памяти и вспомнить, что искомой кривой является циклоида. Как пишет Уайтсайд, Ньютон должен был заметить, что задача схожа с задачей о поиске тела вращения, обладающего наименьшим сопротивлением течению однородного потока. Эту задачу он решил более десяти лет назад, когда работал над «Началами». Но история на этом не заканчивается. Когда Лейбниц представлял полученные решения задачи о брахистохроне, он упомянул, что заранее знал, кому удастся найти решение: «Разумеется, не будет недостойным указать, что задачу удалось решить только тем, на кого я указал наперед. В действительности это те, кто достаточно глубоко проник в тайны нашего дифференциального исчисления. Так, наряду с братом автора [задачи] и маркизом Лопиталем из Франции я упомянул… господина Ньютона». Лейбниц не включил в список Фатио де Дюилье, и, кроме того, из его фразы можно было сделать вывод, что Ньютон является его учеником.Фатио атакует, Лейбниц контратакует
Фатио не смог стерпеть подобной ремарки. Он подготовил ответ и опубликовал его в Лондоне в 1699 году. В нем говорится: «Достопочтенный господин Лейбниц, быть может, задастся вопросом, от кого он узнал об использованном им исчислении. Во всех отношениях его общие принципы и большинство его правил открыл я сам, начиная с апреля 1687 года и в течение последующих лет. В то время я думал, что никто, кроме меня, не использовал это исчисление. Господин Лейбниц не был бы менее неизвестен мне, если бы его вообще не существовало. Он может похвастаться многими учениками, но я не вхожу в их число. Это станет известно, если будут опубликованы письма, которыми я обменивался с достопочтенным господином Гюйгенсом. Однако факты таковы, что первым это исчисление открыл Ньютон много лет назад. Лейбниц, второй, кто открыл исчисление, мог заимствовать что-либо у Ньютона, но это я оставляю на суд тех, кто видел письма господина Ньютона и его рукописи. Ни скромнейшее молчание Ньютона, ни неизменное тщеславие Лейбница, который при каждом удобном случае приписывает себе авторство этого исчисления, не обманут никого, кто изучит доступные материалы подобно тому, как это сделал я». Возможно, дело еще более омрачила дружба Фатио и Ньютона. Лейбниц мог посчитать, что Ньютон убедил Фатио обвинить его в плагиате, хотя Фатио вполне мог действовать самостоятельно, желая понравиться Ньютону. Несмотря на прямое обвинение в плагиате, скандал не спешил разгораться. Лейбниц опубликовал ответ в журнале Acta eruditorum и отметил, что обвинения Фатио могли быть продиктованы кем-то другим: «Прошу простить меня, если не отвечу на все ваши утверждения, пока вы не докажете, что не действуете по чьему-либо указанию, и в особенности по указанию Ньютона, с которым я никогда не враждовал». Лейбниц настаивал на том, что методы анализа были открыты им независимо: «Что же до меня, то я при каждом удобном случае заявлял о его [Ньютона] значительных заслугах, и это известно ему, как никому другому. Он также объявил об этом публично, когда в 1687 году в своих «Началах» опубликовал некоторые свои геометрические открытия, которые совершили мы оба. При этом никто из нас не приписывал себе заслуг другого, но объяснял открытия лишь результатом собственных измышлений, которые я изложил десять лет назад». Решение Ньютона включить в «Оптику» (этот труд был опубликован в 1704 году) два приложения, в особенности то из них, что было посвящено задаче о квадратуре, несомненно, было продиктовано желанием прояснить ситуацию, создавшуюся после обвинений, выдвинутых Фатио. Причиной также были неоспоримые успехи Лейбница в области анализа: благодаря ему и его ученикам, Якобу и Иоганну Бернулли, а также маркизу Лопиталю, математический анализ в последнее десятилетие XVII века превратился в мощное средство, доступное любому желающему изучить его. Как писал Альфред Руперт Холл, автор самого полного исследования, посвященного полемике Ньютона и Лейбница, «наиболее существенные разногласия между ними были связаны с оценкой математического анализа: был ли он всего лишь логичным продолжением уже известных методов анализа или чем-то особенным, радикально отличавшимся от всего, что было известно до этого. Ньютон не считал математический анализ чем-то особенным, хотя, разумеется, осознавал значимость своих открытий. Можно с уверенностью сказать, что не последнюю роль в этом сыграли успех Лейбница и его последующая слава. Лейбниц считал математический анализ гигантским шагом вперед, сравнивая его с появлением алгебры; с созданием анализа математика изменилась бесповоротно». В предисловии к «Оптике» Ньютон объясняет, почему он добавил к своей работе примечания, которые не вошли во второе издание, опубликованное в 1717 году: «В письме, написанном господину Лейбницу… я упомянул о методе, благодаря которому нашел некоторые общие теоремы, связанные с квадратурой криволинейных фигур. <…> Так как несколько лет назад я предоставил ему рукопись, содержащую эти теоремы, а затем обнаружил, что часть ее содержимого была скопирована, я, пользуясь случаем, публикую свою рукопись». Прямое обвинение в плагиате, выдвинутое Ньютоном, было направлено не Лейбницу, а шотландскому врачу Джорджу Чейни, который в 1703 году опубликовал книгу, где перечислил и систематизировал различные результаты, связанные с вычислением квадратур, авторами которых были Ньютон, Лейбниц, Джеймс Грегори, Иоганн Бернулли и Джон Крэг, Лейбниц подготовил краткое изложение «Рассуждения о квадратуре кривых» для Acta eruditorum и опубликовал его без указания имени автора в январе 1705 года. Хотя он впоследствии отрицал авторство этой статьи, один из биографов Лейбница Эдуард Гурауэр в середине XIX века обнаружил рукопись этой статьи с подписью Лейбница. Фраза, ставшая причиной полемики, звучит так: «Когда некая величина изменяется непрерывно, как, например, изменяется линия при движении описывающей ее точки, эти мгновенные изменения называются дифференциалами. <…> И, как следствие, появилось дифференциальное исчисление и обратное ему сумматорное исчисление. Элементы этого исчисления были опубликованы его изобретателем, господином Готфридом Вильгельмом Лейбницем. <…> Вместо дифференциалов Лейбница господин Ньютон применил и всегда применял флюксии. <…> Он элегантно использовал эти флюксии в своих «Математических началах», равно как и Оноре Фабри в своем Sinopsis geometrica заменил последовательное движение по методу Кавальери». Как бы то ни было, эти строки написаны не с целью задеть кого-либо. Тезис «вместо дифференциалов Лейбница господин Ньютон применил и всегда применял флюксии» не предполагает, что дифференциал был открыт раньше, чем флюксия. Тем не менее Лейбниц использует латинское изречение, допускающее двойное толкование: adhibet, semperque adhibuit можно перевести как «применил и всегда применял» или «заменил и всегда заменял». Во втором случае фраза приобретает совершенно другую окраску, которая только усилится, если принять во внимание упоминания о Фабри и Кавальери: Ньютон в этом случае играет роль Фабри, Лейбниц — роль Кавальери. Фабри интерпретировал неделимые Кавальери в терминах флюксий. Не хотел ли Лейбниц сказать, что Ньютон интерпретировал дифференциал, введенный Лейбницем, в терминах флюксий? Возможно, что Лейбниц не осознавал, что его фраза допускает двойное прочтение. По мнению Холла, наиболее вероятно, что он допустил «оговорку по Фрейду». Лейбниц позднее говорил, что это прочтение его слов было вызвано исключительно желанием развязать ссору. Он прояснил, что кто бы ни был автором этого документа, он использовал выражение adhibuit применительно к Ньютону, а применительно к Фабри использовал substituit. Следовательно, в случае Ньютона слово adhibuit следует понимать как «применять», и эти глаголы по отношению к Ньютону и Фабри употреблялись в совершенно разном смысле. Таким образом, не могло идти речи о каком-либо их сравнении. Как видим, стороны подробно рассматривали каждое слово, словно речь шла о городской войне дом на дом или улица на улицу. Статья Лейбница сначала осталась без ответа. Возможно, Ньютон и его сторонники не сразу распознали двойное толкование фразы или, что более вероятно, они попросту не читали статью.ОТВЕТ ЧЕЙНИ
Когда Ньютон в своей «Оптике» указал, что некоторые из его результатов были «скопированы», он имел в виду книгу Джорджа Чейни. Однако эта ремарка несколько несправедлива, поскольку Чейни не только скопировал результаты Ньютона, но и высказал похвалу в его адрес и совершенно искренне отметил: «Заявляю, что все, что было опубликовано другими приблизительно за последние 24 года касаемо этих и других схожих методов, является лишь повторением или следствием того, что господин Ньютон сообщил своим друзьям или опубликовал». На эти слова Лейбниц строго возразил: «Вы неумело пытаетесь приписать Ньютону авторство метода рядов с неопределенными коэффициентами, которые определяются путем сравнения членов ряда. Однако я опубликовал этот метод [в 1693 году], когда ни я, ни кто-либо другой, по меньшей мере публично, не заявлял о том, что господин Ньютон создал этот метод». И еще: «Возможно, господин Ньютон совершил некоторые открытия раньше, чем я, равно как и я совершил некоторые открытия раньше него. Разумеется, я не встретил никаких указаний на то, что ему было известно дифференциальное исчисление или нечто подобное раньше, чем мне».
Появление «обезьяны Ньютона»
Тем не менее три года спустя ответ последовал. Он был подписан именем шотландского математика Джона Кейля, который, скорее всего, стал неустанным автором нападок на Лейбница по решению самого Ньютона: «Боевой конь, — как пишет Ф. Мэнюэль, — столь ярый, что Ньютону порой приходилось натягивать вожжи». Иоганн Бернулли называл Кейля «обезьяной Ньютона». Хотя английское слово «аре», которое использовал Бернулли, также можно перевести как «подражатель», мы предпочли буквальный перевод, так как именно это значение имел в виду сам Бернулли.ДЖОН КЕЙЛЬ (1671-1721)
Джон Кейль родился в декабре 1671 года в Эдинбурге. Он учился в Эдинбургском университете, где его наставником был Давид Грегори. Кейль находился в первых рядах сторонников недавно опубликованной ньютоновской философии. Он окончил Оксфорд, куда перешел при содействии Грегори, когда тот возглавил кафедру в этом университете. Кейль занимал этот пост с 1712 года до своей смерти в августе 1721 года. Он был избран членом Королевского общества в 1700 году. Кейль неустанно пропагандировал философию Ньютона, занимая в группе его сторонников особое место, будучи наиболее ярым участником дискуссий.
В начале 1709 года Кейль на страницах «Философских записок» обвинил Лейбница в плагиате: «Все эти предположения являются следствием известнейшей арифметики флюксий, которую, вне всяких сомнений, первым изобрел доктор Ньютон, в чем легко может убедиться всякий, кто ознакомится с письмами, опубликованными Валлисом. Эта же арифметика, но под другим названием и с другими обозначениями была впоследствии опубликована доктором Лейбницем». «Философские записки» были журналом Лондонского королевского общества, поэтому обвинение в адрес Лейбница прозвучало, можно сказать, от имени всего Королевского общества. Поскольку Лейбниц, начиная со своего первого визита в Лондон в 1673 году, был членом Общества, в 1711 году он потребовал опровержения заметки Кейля. Лейбниц, скорее всего, не осознавал, что на спор об авторстве анализа бесконечно малых оказали влияние критики метафизических основ ньютоновской теории тяготения, принадлежавшие к числу сторонников Лейбница. С подобной критикой порой выступал и сам Лейбниц. К сожалению для него, когда он попросил защиты и поддержки в Королевском обществе, президентом которого был Ньютон, то не совсем понимал, что спор осложнит националистская подоплека и критика теории тяготения Ньютона, с которой выступали ученые континентальной Европы. Националистский подтекст прямо или косвенно присутствует во многих письмах и документах, опубликованных участниками спора. Например, Уильям Джонс в 1711 году писал Роджеру Котсу: «Мне особенно не о чем вам рассказать, разве что немцы и французы нападают на философию сэра Исаака Ньютона…». Лейбниц писал Иоганну Бернулли в 1713 году: «Уже много лет тщеславные и напыщенные англичане, включая достойнейших из них, не теряют возможности лишить авторства немцев и выдать их открытия за свои. <…> Теперь они хотят лишить Николаса Меркатора из Гольштейна славы первооткрывателя ряда и раздосадованы мной, поскольку я защищаю прекрасного человека и моего друга».

Гравюра, на которой изображено заседание Королевского общества, президентом которого был Ньютон, в Крейн-Корт.
Вместо письма с объяснениями, которое Лейбниц попросил у Кейля, он получил совершенно иной ответ. На очередном заседании общества 24 мая 1711 года под руководством Ньютона были зачитаны новые обвинения, выдвинутые Кейлем в адрес Лейбница. Кейль писал: «Разумеется, заслуги Лейбница в области познания огромны, я признаю это, равно как и никто, кто прочел его труды, не может отрицать, что Лейбниц является экспертом в самых непонятных разделах математики. Поскольку он обладает столь неоспоримыми достоинствами, я не понимаю, почему он желает отнять заслуги других. <…> Так, поскольку этот блестящий персонаж подал апелляцию в Королевское общество и желает, чтобы я публично признал, что не имел намерений оклеветать его, я должен показать, чтобы снять с себя обвинения, что господин Ньютон является первым и истинным изобретателем арифметики флюксий, или дифференциального исчисления, что он отправил четкие и понятные указания по этому методу господину Лейбницу, и последнему не составило труда создать аналогичный метод».Лейбниц попадает в недобрые руки Королевского общества
Когда Лейбниц получил письмо Кейля, то написал ответ, признавая, что математический анализ был открыт совместно: «Нет причины, по которой вам следовало бы сообщить, опровергнув восстановленный им [Кейлем] мой способ познания вещей, тому, который не имеет достаточно опыта, чтобы судить о том, как совершаются открытия. Моим друзьям известно, что я следовал своим путем и преследовал другие цели. С вашей стороны бессмысленно приводить в пример журнал Acta из Лейпцига в оправдание ваших слов, поскольку я не нахожу в нем ничего, что я позаимствовал бы у кого-либо. Напротив, каждому воздается по его заслугам. Я и мои друзья в различных случаях заявляли, что блестящий первооткрыватель флюксий совершил открытие собственными силами, использовав те же базовые принципы, что и мы. У меня есть не меньше прав, чем у него [Ньютона] заявлять, что именно я являюсь автором открытия». Лейбниц обратился в Королевское общество с просьбой защитить его от нападок Кейля: «Я взываю к вашему чувству справедливости, чтобы решить, следует ли прекратить пустые и несправедливые оскорбления или нет. Считаю, что сам Ньютон не одобрил бы этого, поскольку он является достойным человеком и знаком с истинным положением дел. Надеюсь, что он свободно выскажет свое мнение по этому вопросу». Следует привести мнение Ньютона о тех, кто совершил открытие с опозданием: «У того, кто совершил открытие вторым, нет прав на него. Единственное право принадлежит первооткрывателю, даже если второй совершил открытие независимо от него. Взять права первооткрывателя и разделить их между ними было бы несправедливо». Более того: «Тот, кто совершил открытие вторым, недостоин чести. У него нет прав и титулов. Что же мы в этом случае можем сказать о тех, кто даже не может с определенностью доказать, что именно они совершили открытие вторыми?» Судьба Лейбница была предрешена. Чтобы успокоить спорящих, пишет Вестфолл, «Лейбниц предложил неожиданное решение для Ньютона и сам воззвал к справедливости Королевского общества. Точку в этом вопросе должно было поставить Общество». Была создана комиссия из друзей и защитников Ньютона. Чтобы создать какое-то подобие беспристрастности, в комиссию также вошел представитель Пруссии в Лондоне. Однако он стал членом комиссии лишь за неделю до того, как был вынесен окончательный вердикт, и, следовательно, не принимал особого участия в работе. Состав комиссии держался в секрете и стал известен лишь в середине XIX века. Чтобы проверить все документы и вынести вердикт, комиссии потребовалось 50 дней. Итоговое заключение практически полностью составил сам Ньютон. Оно содержало четыре пункта и хотя не включало явных обвинений в плагиате в адрес Лейбница, в нем выражались достаточные сомнения, чтобы можно было сделать именно такой вывод. Последний пункт гласил: «Дифференциальный метод есть то же, что и метод флюксий, за исключением названия и нотаций. Господин Лейбниц назвал дифференциалами величины, которые господин Ньютон назвал моментами, или флюксиями, и обозначил их буквой d, в то время как господин Ньютон это обозначение не использовал. Поэтому мы считаем, что будет правильнее рассматривать вопрос не о том, кто открыл тот или иной метод, а о том, кто является первооткрывателем этого метода. Мы считаем, что те, кто считают господина Лейбница первооткрывателем, недостаточно осведомлены или не осведомлены вовсе о переписке, которую он вел много лет назад с господином Коллинзом и господином Ольденбургом, а также о том, что господин Ньютон создал этот метод за 15 лет дотого, как господин Лейбниц опубликовал его в Acta eruditorum. По этим причинам мы признаем, что первооткрывателем является Ньютон, и считаем, что господин Кейль, утверждавший это же самое, не нанес господину Лейбницу никакого оскорбления». Вердикт комиссии был дополнен документами и письмами, которые в нем упоминались (они были соответствующим образом отредактированы в интересах Ньютона), и опубликован Королевским обществом под названием Commercium epistolicum D. Johannis Collins, et aliorum de analysi promota в 1712 году. Было сделано несколько копий, которые не поступили в продажу, а были целенаправленно разосланы определенным людям. В 1722 году, спустя шесть лет после смерти Лейбница, Ньютон выпустил второе, расширенное издание, которое на этот раз поступило в продажу. Commercium epistolicum был дополнен предисловием Ньютона, в котором «для удобства читателя» излагалась суть диспута. «Если бы вы действовали по справедливости, вы уведомили бы меня о том, что Общество собирается подробно рассмотреть этот вопрос, — жаловался Лейбниц спустя полтора года после публикации этого однобокого заключения комиссии. — Вы должны были предоставить мне возможность изложить мою точку зрения и сообщить, не считаю ли я подозрительным кого-либо из судей. Вердикт был вынесен после того, как была выслушана лишь одна из сторон, поэтому заключение очевидно недействительно». Документы, включенные в Commercium epistolicum, по разным причинам неадекватно отражали суть спора и поставили Лейбница в очень неудобное положение. Иоганн Бернулли заподозрил, что документы могли быть подделаны, о чем он уведомил Лейбница в 1714 году: «Некоторые из этих писем, изложенные в Commercium epistolicum, кажутся мне очень подозрительными. Если они не полностью сфабрикованы, то по меньшей мере отредактированы и фальсифицированы». Лишь в середине XIX века, когда было выпущено собрание математических трудов Лейбница, появилось документальное подтверждение тому, что он совершил открытие анализа независимо от Ньютона. В некотором роде Commercium epistolicum и математические труды Ньютона, опубликованные с опозданием в начале XVIII века, склонили чашу весов на сторону Ньютона. Тем не менее в математическом споре победу одержал Лейбниц: благодаря своим последователям братьям Бернулли, а затем Эйлеру дифференциальное исчисление Лейбница совершило триумфальное шествие на протяжении XVIII века, и в начале XIX века даже англичане признавали преимущество математиков континентальной Европы.ОДИН СПОР, ДВЕ ТОЧКИ ЗРЕНИЯ
Ньютон неизменно придавал дискуссии драматизм. Причиной этому, по мнению Ф. Мэнюэля, была травма, нанесенная ему разрывом с матерью в детстве: «Когда у него пытались что-то отнять, он реагировал неистово и с ненавистью, вызванной этой первой и серьезной потерей». Лейбниц также очень серьезно относился к спору, однако при случае позволял себе упоминать о нем в шутливой форме: «Невозможно сообщить полную информацию вкратце и невозможно избежать того, что судьи часто зевают, когда рассматривается столь длительное и объемное дело, как наше. Однако… можно поступить подобно обувщику из Лейдена… Он не упускал случая посетить публичные диспуты в Университете. Наконец кто-то из его знакомых спросил, знает ли он латынь. «Нет, — ответил он,- и я не возьму на себя труд изучить ее». — «Но почему вы неизменно приходите в эту аудиторию, где все дискуссии ведутся на латыни?» — «Поскольку мне нравится быть судьей в спорах».- «Но как вы можете судить, если не знаете, о чем идет речь?» — «У меня есть другой способ определить, на чьей стороне правда».- «Каков же этот способ?» — «Когда я вижу, как кто-то сердится и впадает в ярость, я заключаю, что он неправ».
Charta volans и «ведущий математик»
Лейбниц ответил на Commercium epistolicum почти год спустя в форме анонимного письма против Ньютона, озаглавленного Charta volans — «Летучий листок». В письме выдвинуты обвинения в плагиате в адрес Ньютона. В частности, указывалось, что он создал метод флюксий на основе изложенного в письмах Лейбница, отправленных в ответ на Epistolae prior и Epistolae posterior. Лейбниц составил план Charta volans после того, как получил письмо Иоганна Бернулли, где сообщалось о выпуске Commercium и выдвигались обвинения в плагиате в адрес Ньютона. Лейбниц процитировал письмо Бернулли в Charta volans, приписав авторство неизвестному «ведущему математику». Иоганн Бернулли сыграл очень важную роль в споре. Его поведение было отчасти противоречивым: он настраивал Лейбница против его оппонента и в то же время сохранял нейтральный тон в письмах к Ньютону и его друзьям. Когда Лейбниц включил в Charta volans цитату из письма Бернулли (хотя тот просил не вовлекать его в спор с Ньютоном), его двойная игра раскрылась. После того как Лейбниц вольно или невольно допустил такую бестактность, особенно четко стало понятно, какую игру вел Бернулли, когда в декабре 1715 года тот опубликовал второе письмо, где назвал имя «ведущего математика» из Charta volans. О поведении Иоганна Бернулли в ходе спора можно судить по его переписке с Ньютоном в 1719 году и по тому, как он объясняет письмо «ведущего математика», которое Лейбниц включил в Charta volans. В этом письме говорилось: «Я не знаю, как это произошло, однако после того как несколько лет назад произошел этот ожесточенный спор между геометрами Британии и Германии, к стыду математической науки, я, не будучи ни британцем, ни немцем, а швейцарцем, был далек от того, чтобы принять чью-то сторону, поскольку я редко по своей воле участвую в спорах других, и потерял ваше расположение, о чем ходят различные слухи. <…> Посему у меня нет сомнений, достопочтенный сэр, что вам сообщили множество лжи и выдумок обо мне, которые повредили моей репутации в ваших глазах либо уничтожили ее вовсе. <…> Я отзывался с похвалой о вас и ваших открытиях всякий раз, когда на то представлялась возможность: чего же более мог сделать тот, кто считает ваши заслуги величайшими? Я восторженно превозносил их при каждом удобном случае в моих письмах, речах, классах и беседах, что могут подтвердить мои адресаты и слушатели. <…> Вне всяких сомнений, ошибаются те, кто сообщил, что я являюсь автором писем, в которых, возможно, ваше имя упоминается в недостаточно почтительном тоне, однако умоляю вас, знаменитый сэр, во имя всего святого для человечества, чтобы вы уверились в том, что подобные анонимные письма приписываются мне по ошибке. Поскольку не в моих привычках публиковать без подписи то, что я не желаю и не осмеливаюсь признавать своим». В декабре 1719 года Бернулли, думая, что, возможно, ему удастся получить доступ к документам покойного Лейбница и рассказать всем о письме, которое Лейбниц процитировал в Charta volans и в котором Бернулли действительно отзывается о Ньютоне не в самой лестной форме, он снова пишет Ньютону с несравненным нахальством: «Не помню, чтобы я писал господину Лейбницу в тот день, хотя и не могу отрицать этого, поскольку не располагаю копиями всех писем, написанных мною. Однако если бы среди многочисленных писем, написанных ему, было бы найдено письмо, отправленное точно в этот день и год, то я со всей уверенностью утверждал бы, что ничего из содержащегося в письме никоим образом не пошатнет вашу репутацию. И я никогда не давал разрешения [Лейбницу], и он публиковал определенные письма, в особенности те, которые пришлись бы вам не по душе, против моей воли и желания».Лев точит когти
Ньютон собственноручно полностью переписал всё Charta volans, словно оскорбления Лейбница заряжали его некой энергией и обостряли желание мстить. Он хотел лично ответить на Charta volans и в 1714 году подготовил ответ. Однако в конечном итоге это письмо не было отправлено, и Ньютон предпочел настроить Кейля против Лейбница. Ответ Ньютона на Charta volans носил название Account. Это анонимное письмо представляло собой сжатое изложение Commercium epistolicum и было опубликовано на английском языке в «Философских записках» в 1715 году. Также сохранились рукописи этого письма, собственноручно написанного Ньютоном, которые более или менее близки к опубликованной версии. Это письмо — прекрасное доказательство одержимости, которую Ньютон испытывал в наиболее ожесточенный период спора, с 1712 по 1716 год, а также некоторое время после смерти Лейбница. Ньютон чувствовал неутолимое желание изложить свою версию событий, снова и снова выступить против Лейбница. Ньютон как одержимый писал письма, меморандумы, заметки, которые редактировал снова и снова, исправляя отдельные фразы то тут, то там, добавляя цитаты и вставляя всё новые оскорбления. Практически все эти документы (многочисленные варианты писем, которые он так и не отправил) были опубликованы в приложениях к его трудам, выпущенным после смерти оппонента. Эти письма словно немые свидетели того, как трудно было Ньютону сдерживать свой гнев. Предполагалось, что Account будет опубликован без подписи, хотя лишь немногие сомневались в том, кому принадлежит авторство. Этот документ — длинное, жесткое и клеветническое письмо, направленное против Лейбница. Ньютон считал, что документов, процитированных в Commercium epistolicum, недостаточно, поэтому переиначил их по-своему и, таким образом, аргументировал свои нападки на Лейбница и его друзей. На трех последних страницах Account Ньютон ведет речь о критиках его теории тяготения, которую, согласно Лейбницу, Ньютон описал как таинственное и загадочное свойство, подобное тому, которым схоласты объясняли движение тел. Ньютон понимал, что в его трудах не раскрывалась природа гравитации, и был недоволен тем, что сила тяготения в его теории действовала на расстоянии и даже в пустоте, однако не хотел отступаться от своей концепции. Он объясняет это в приложении ко второму изданию «Начал»: «Причину же этих свойств силы тяготения я до сих пор не мог вывести из явлений; гипотез же я не измышляю. Все же, что не выводится из явлений, должно называться гипотезою; гипотезам же метафизическим, физическим, механическим, скрытым свойствам не место в экспериментальной философии. <… > Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам. Этого вполне достаточно для объяснения всех движений небесных тел и моря».БОГ — НЕ ЧАСОВОЙ МАСТЕР
Помимо спора о том, кто первым открыл математический анализ, в ноябре 1715 — октябре 1716 года (Лейбниц умер в ноябре 1716-го) разгорелся интересный философский спор между Сэмюелом Кларком и Лейбницем о метафизике и естественной философии. Поводом к спору послужила высказанная Лейбницем критика метафизической стороны теории тяготения и роли Бога в ньютоновской философии, В этом споре Ньютон встал на сторону Кларка (однако не инструктировал его так, как Кейля), но всегда жаловался, что Лейбниц хотел перевести спор о первенстве открытия анализа в метафизическую плоскость, где немецкий математик чувствовал себя намного увереннее: «Ньютон не слишком успешен в метафизике»,- сказал как-то Лейбниц. Лейбниц заострял внимание на фрагментах «Оптики», из которых следовало, что Бог должен вмешиваться в движение небесных тел, чтобы звезды не упали друг на друга и чтобы планеты Солнечной системы не сходили с орбит, подобно тому как часовщик время от времени подводит часы. Он жестко критиковал эту позицию: «Господин Ньютон и его последователи имеют прекрасное мнение о Божьем творении, Они считают, что Бог должен время от времени подводить свои часы, иначе они остановятся. Это Божье творение столь несовершенно, что требуется помощь извне, чтобы настроить или починить его, подобно тому как поступает со своим творением часовой мастер».
Лейбниц пытался ответить на Account, изложив свою версию событий под заглавием Historia et origo calculi differentialis, однако вскоре увидел, что ему не удастся составить столь же полный, подробный и изобилующий письмами и документами труд, как ньютоновский Commercium. Об этом он говорит в присущей ему манере на первых страницах Historia et origo: «Будучи в отъезде, когда это было опубликовано моими противниками, вернувшись два года спустя, я был занят другими делами и не смог ни получить обратно моих старых писем, ни ознакомиться с теми из них, где сам он рассказывает о том, что произошло уже более 40 лет назад. У меня не сохранилось копий старых писем и других ваших рукописей». Нужно признать, что составить столь подробный труд, основанный на старых документах, Лейбницу было намного сложнее, чем Ньютону. Среди множества причин отметим неимоверный объем корреспонденции, отправленной Лейбницем в течение всей жизни, который был на порядок больше, чем у Ньютона. Поэтому совершенно убедительным выглядит оправдание Лейбница, где он указывает, что не смог найти своих писем: «Чтобы подробным образом ответить на труд, опубликованный против меня… мне пришлось бы отыскать мои старые письма, некоторые из которых утеряны. Помимо этого, во многих случаях я не сохранял черновиков. Другие письма похоронены под горой бумаг, для упорядочения которых мне потребуется много времени и терпения». Следовательно, Historia et origo, в отличие от Account, является в большей степени результатом воспоминаний Лейбница. Возможно, Лейбниц планировал расширить и дополнить его, однако смерть, настигшая его в ноябре 1716 года, помешала ему завершить начатое. Historia et origo не была опубликована во время спора и увидела свет лишь 130 лет спустя, в 1846 году.
Как покровитель Лейбница стал королем Ньютона
Примечательные, но безуспешные попытки примирить Ньютона и Лейбница пред приняли Джон Чемберлен и аббат Конти в период с 1714 по 1715 год. Чемберлен и Конти очень отличались друг от друга. Первый был членом Королевского общества и политиком, переписывался с Лейбницем с 1710 года и поддерживал хорошие от ношения с Ньютоном. Антонио Конти, в свою очередь, был священником в городе Падуя, прибыл в Англию для наблюдения солнечного затмения и задержался на несколько лет. Он поддерживал хорошие отношения с Лейбницем и благодаря «пленительному» характеру завязал дружбу с Ньютоном. Ф. Мэнюэль пишет: «Конти был одной из тех пышных и ловких личностей интеллектуального мира XVIII века, стихоплетом, актером, переводчиком Расина и Поупа, любителем наук, дилетантом, который с одинаковой ловкостью интриговал принцесс и философов Англии, Франции, Германии и Италии». Интерес представляла его политическая деятельность в родной Падуе, где не было недостатка ни в принцессах, ни в философах.
Статуя аббата Конти, воздвигнутая в 1781 году.
С одной стороны, Чемберлена, имевшего связи в королевском дворе, беспокоило, что Лейбниц был советником герцога Брауншвейгского, который вскоре должен был переехать в Англию. Об этом он сообщил Ньютону в мае 1714 года: «Мне очень жаль, что я не смог встретиться с вами этим вечером, чтобы рассмотреть письмо о вас, которое мне отправил господин Лейбниц. <…> Согласен с тем, чтобы вы использовали это письмо по вашему разумению, но проявите должное благоразумие, какое следует проявить с этим человеком, поскольку Лейбница очень высоко ценят при дворе ганноверской династии». Вмешательство Чемберлена кончилось тем, что у них с Ньютоном возникли разногласия, и это стоило ему дружбы с математиком. Как пишет Вестфолл: «Благословенны примирители, ибо на них обращается вражда обеих сторон». Восшествие Георга I, покровителя Лейбница, на трон Великобритании и Ирландии, по сути, не могло благоприятно сказаться на ходе спора: «С легкостью могу поверить, — писал Иоганн Бернулли, — что после того как ваш достопочтенный принц взойдет на трон Великобритании, Королевское общество выскажется против того, чтобы ваше имя было опубликовано в Commercium epistolicum. <…> Возможно, даже Кейль не хотел, чтобы его памфлет был опубликован, если бы предчувствовал перемены в британской политике, произошедшие несколько позднее». Сам Кейль в письме к Ньютону, написанном в ноябре 1714 года спустя несколько месяцев после смерти королевы Анны, высказал некоторую озабоченность в связи с тем, что Лейбниц приедет в Англию вместе с новым королем: «Надеюсь, что господин Лейбниц… поступит осмотрительно и не покажется в Англии. Если же он сделает это, я убежден, что не встретит здесь много друзей». Лейбниц также ожидал, что король встанет на его сторону в споре. Правда, отношения со своим покровителем всегда складывались у него не лучшим образом, хотя к нему прекрасно относилась София, мать короля, и Каролина, жена его сына, которая при восшествии Георга на престол стала принцессой Уэльской. Однако король, по-видимому, не проявил ни малейшего интереса к спору Ньютона и Лейбница. Тем не менее аббату Конти удалось, пусть и косвенно, сообщить об этом вопросе новому королю Англии Георгу I, а также представителям ганноверской династии при королевском дворе в Лондоне. Вместе с другими представителями знати на одной из встреч они изучили документы Ньютона, посвященные диспуту, и постановили, что Ньютон должен изложить свою версию событий в письме Лейбницу. Письмо должно было быть одобрено королем, а Лейбниц должен был в ответ направить свою версию. Таким образом, начался последний обмен письмами между Ньютоном и Лейбницем. Ситуация постепенно накалялась, и попытка примирить ученых чуть было не усугубила противостояние. Со смертью Лейбница 14 ноября 1716 года накал страстей несколько утих и вместе с тем исчезли немногие возможности уладить спор. Ньютон, продемонстрировав всю мстительность, после смерти Лейбница опубликовал их последнюю переписку и «Наблюдения» по поводу последнего письма Лейбница. «Лейбниц умер — диспут окончен», — написал аббат Конти Ньютону 10 декабря 1716 года. Тем не менее он погрешил против истины: с уходом одного из оппонентов диспут не прекратился, так как наиболее ярые участники с обеих сторон — Джон Кейль, «обезьяна Ньютона», и Иоганн Бернулли, «ведущий математик», друг и ученик Лейбница, были живы (Кейль умер в 1721-м, Бернулли — в 1748 году). Не будем забывать и о Ньютоне, который пережил Лейбница на 10 лет, первые шесть из которых его сильнее всего заботил неоконченный диспут. Он продолжал писать всё новые и новые труды о праве на авторство математического анализа, о том, что говорилось в старых письмах и документах, о том, насколько подло поступали те, кто хотел воспользоваться его открытиями или критиковал его науку. Эти труды по большей части были неотредактированными, подобно множеству других работ Ньютона, посвященных математике, алхимии, богословию, истории… Ньютон собственноручно составил список наблюдений, поставив под сомнение и ревностно отцензурировав хвалебные слова Кристиана Вольфа в адрес Лейбница, опубликованные после его смерти в Acta eruditorum, и некролог Лейбницу, написанный Фонтенелем, секретарем Парижской академии наук. «Мораль пуританского мира, — пишет Ф. Мэнюэль, — подобно любой христианской морали предписывает любить Бога и ближнего своего. К этим двум принципам Ньютон сводил всю религию. Однако в пуританстве также предписывалось искоренять зло. Любить и разрушать — такой была противоречивая догма».Глава 6. Укрощенные бесконечно малые
Бесконечности, большие и малые
Анализ бесконечно малых был наполнен бесконечно большими и бесконечно малыми величинами с самого момента создания, в течение первых трех четвертей XVII века, когда его продвинули вперед Ньютон и Лейбниц, равно как и позднее, в течение всего XVIII века. Бесконечно малая величина — это числовая функция или последовательность, которая стремится к нулю. Так как она не является строго равной нулю, ее можно использовать в знаменателе дроби, а так как она является бесконечно малой, ее можно принять равной нулю, когда мы хотим упростить выражение. Бесконечно большая величина, в свою очередь, остается неизменной, когда мы прибавляем к ней обычное число. Иными словами, если N — бесконечно большая величина, то выполняется достаточно необычное равенство: N + 1 = N. Разумеется, из-за этих необычных свойств существование бесконечно больших и бесконечно малых неоднократно ставилось под сомнение. Анализ бесконечно малых регулярно критиковался из-за того, что он был основан на бесконечно малых величинах. Критики задавались вопросом: как можно получить верный результат с помощью метода, в основе которого лежит понятие, столь нечеткое с точки зрения логики? Математики, которые начали использовать бесконечно малые в XVII веке, — Кеплер, Кавальери, Ферма, Валлис, Паскаль, Барроу (этот список далеко не полон), много раз указывали, что подобные рассуждения приводил еще Архимед. Однако они не утруждали себя написанием строгих доказательств — в отличие от Архимеда. Известные в то время труды Архимеда были опубликованы в середине XVI века, и прошло почти 50 лет, прежде чем математики того времени смогли понять и применить его непростые методы. Архимед был наиболее цитируемым автором в течение всего XVII века. Как мы уже говорили в главе 2, математики этого периода очищали методы Архимеда от геометрической «оболочки» и приводили их в арифметическом и алгебраическом виде. Эти разделы математики набирали популярность в течение XVII века, особенно после открытия аналитической геометрии Декартом и Ферма. В то время математиков больше интересовали открытия, которые можно совершить, используя необычные свойства бесконечно малых, и они не тратили время на построение строгих геометрических доказательств. Во многих случаях подобное пренебрежение строгостью объяснялось попросту нежеланием заниматься излишней работой: «Всё это можно доказать, используя архимедовы техники, однако это потребует больших усилий», — писал Кавальери в 1635 году.Ньютон, Лейбниц и бесконечно малые
Даже создатели математического анализа не приводили исчерпывающих доказательств открытых ими методов. И Ньютон, и Лейбниц осознавали недостаток логики в своих работах и пытались каждый по-своему если не устранить, то хотя бы смягчить этот недостаток. Так, Ньютон попытался избежать использования бесконечно малых путем перехода к пределу, однако потерпел неудачу. Тем не менее его усилия стали источником вдохновения для Коши. Покажем, как следует понимать дробь 0/0, получаемую при h = 0 в выражении необходимом для определения производной f(x) функции f в точке х. Здесь мы позволим себе небольшой анахронизм. Сам Ньютон никогда не использовал понятие производной функции, равно как и не использовал подобные обозначения, а вместо этого употреблял понятие «исчезающая величина». Таким образом, разность f(x + h) — f(x) и само число h будут исчезающими величинами: обе они «исчезают», когда h становится равным нулю. «Последним отношением исчезающих величин» он называл значение вышеуказанной дроби при h = 0. Очевидно, что Ньютон имеет в виду переход к пределу, когда говорит о «последнем отношении исчезающих величин», чтобы обосновать неопределенность 0/0, к которой сводится вышеприведенная дробь при h = 0. Однако он так и не дал этому методу строгого определения. Сам Ньютон осознавал этот недостаток и в объяснении прибегал к физическим аналогиям: «Вероятно, вы можете возразить, что последнего отношения исчезающих величин не существует, поскольку до того как величины исчезают, отношение не является последним, а когда величины исчезают, никакого отношения не существует. Однако, следуя этой же логике, можно отрицать, что тело, которое прибыло в определенную точку и остановилось в ней, не имеет последней скорости, поскольку до этого его скорость не была последней, а после того как тело прибыло в эту точку, его скорость равна нулю. Однако ответ на этот вопрос крайне прост. Под последней скоростью понимается скорость, с которой движется тело в самый момент прибытия, не раньше и не позже, то есть скорость, с которой тело прибыло в последнюю точку и с которой его движение прекратилось. Этим же образом под последним отношением следует понимать отношение величин не до того, как они исчезнут, и не после того, как они исчезнут, а отношение, при котором они исчезнут».
Бесконечно малые величины играли в математическом анализе Лейбница заметно большую роль. Например, они фигурировали в самом определении кривой, которым пользовался Лейбниц. Для Ньютона кривая была образована точкой в движении: «Полагаю математические величины не состоящими из очень малых частей, а описываемыми непрерывным движением. Кривые, таким образом, описываются и создаются не расположением частей, а непрерывным движением точек». Лейбниц же считал, что кривые состоят из отрезков прямой бесконечно малой длины: «Чтобы найти касательную, надо провести прямую, соединяющую две точки кривой, расположенных на бесконечно малом расстоянии, или продленную сторону многоугольника с бесконечным числом углов, который для нас равносилен кривой», — писал Лейбниц в 1684 году.
Понятие кривой еще более четко описывается в книге «Анализ бесконечно малых» маркиза Лопиталя (1696). Второй постулат книги звучит так: «Будем предполагать, что кривую линию можно считать состоящей из бесконечного числа бесконечно малых линий, или, что аналогично, многоугольником с бесконечным числом сторон, каждая из которых имеет бесконечно малую длину, а кривизна линии определяется углами между этими сторонами».
необходимом для определения производной f(x) функции f в точке х. Здесь мы позволим себе небольшой анахронизм. Сам Ньютон никогда не использовал понятие производной функции, равно как и не использовал подобные обозначения, а вместо этого употреблял понятие «исчезающая величина». Таким образом, разность f(x + h) — f(x) и само число h будут исчезающими величинами: обе они «исчезают», когда h становится равным нулю. «Последним отношением исчезающих величин» он называл значение вышеуказанной дроби при h = 0. Очевидно, что Ньютон имеет в виду переход к пределу, когда говорит о «последнем отношении исчезающих величин», чтобы обосновать неопределенность 0/0, к которой сводится вышеприведенная дробь при h = 0. Однако он так и не дал этому методу строгого определения. Сам Ньютон осознавал этот недостаток и в объяснении прибегал к физическим аналогиям: «Вероятно, вы можете возразить, что последнего отношения исчезающих величин не существует, поскольку до того как величины исчезают, отношение не является последним, а когда величины исчезают, никакого отношения не существует. Однако, следуя этой же логике, можно отрицать, что тело, которое прибыло в определенную точку и остановилось в ней, не имеет последней скорости, поскольку до этого его скорость не была последней, а после того как тело прибыло в эту точку, его скорость равна нулю. Однако ответ на этот вопрос крайне прост. Под последней скоростью понимается скорость, с которой движется тело в самый момент прибытия, не раньше и не позже, то есть скорость, с которой тело прибыло в последнюю точку и с которой его движение прекратилось. Этим же образом под последним отношением следует понимать отношение величин не до того, как они исчезнут, и не после того, как они исчезнут, а отношение, при котором они исчезнут».
Бесконечно малые величины играли в математическом анализе Лейбница заметно большую роль. Например, они фигурировали в самом определении кривой, которым пользовался Лейбниц. Для Ньютона кривая была образована точкой в движении: «Полагаю математические величины не состоящими из очень малых частей, а описываемыми непрерывным движением. Кривые, таким образом, описываются и создаются не расположением частей, а непрерывным движением точек». Лейбниц же считал, что кривые состоят из отрезков прямой бесконечно малой длины: «Чтобы найти касательную, надо провести прямую, соединяющую две точки кривой, расположенных на бесконечно малом расстоянии, или продленную сторону многоугольника с бесконечным числом углов, который для нас равносилен кривой», — писал Лейбниц в 1684 году.
Понятие кривой еще более четко описывается в книге «Анализ бесконечно малых» маркиза Лопиталя (1696). Второй постулат книги звучит так: «Будем предполагать, что кривую линию можно считать состоящей из бесконечного числа бесконечно малых линий, или, что аналогично, многоугольником с бесконечным числом сторон, каждая из которых имеет бесконечно малую длину, а кривизна линии определяется углами между этими сторонами».

«Анализ бесконечно малых» маркиза Лопиталя, первая книга по анализу бесконечно малых Лейбница.
Лейбниц объяснял использование бесконечно малых подобно своим предшественникам: «Выбираются столь большие или столь малые величины, чтобы ошибка была меньше данной, так что различия с методом Архимеда заключаются лишь в способе записи, но наш метод более соответствует духу изобретательства». Лейбниц попал в самую точку: в то время ученых больше интересовали открытия, а не доказательства.ЭДМУНД ГАЛЛЕЙ, НЕВЕРУЮЩИЙ
Книга Беркли «Аналитик» имела подзаголовок: «Трактат, адресованный неверующему математику». Этим «неверующим математиком», скорее всего, был астроном Эдмунд Галлей, который всегда славился атеистическими взглядами и как-то заставил больного отказаться от посещения епископа Беркли, убедив его в непрочности доктрин христианства. В своей книге Беркли хотел показать, что рассуждения анализа бесконечно малых столь же непрочны, как и религиозные догмы. Второй подзаголовок книги звучит так; …где исследуется, является ли предмет, принципы и заключения более отчетливо познаваемыми и с очевидностью выводимыми, чем религиозные таинства и положения веры». Он добавлял: «Извлеки бревно из глаза своего, и сможешь извлечь соринку из глаза брата твоего». В своей книге Беркли также приводит ряд вопросов, над которыми полагается размышлять. Процитируем некоторые из них: «Вопрос 62. Разве непостижимые тайны не могут с большим правом допускаться в божественной вере, чем в человеческой науке? Вопрос 63. Разве те математики, которые резко выступают против непостижимых тайн, когда-либо критически исследовали собственные принципы?»
«Призраки исчезнувших величин»
Несмотря на огромный шаг вперед, который позволил совершить анализ бесконечно малых Ньютона и Лейбница, критика в адрес недостаточной прочности его основ была обоснованной. Наиболее ярым критиком был английский епископ и философ Джордж Беркли. В 1734 году он опубликовал книгу под названием «Аналитик», где в критическом духе были рассмотрены основные идеи анализа с целью продемонстрировать их недостаточную логичность. Так, Беркли заявил, что вывод формулы для вычисления производной произведения, приведенный Ньютоном в «Началах» (см. главу 3), был ошибочным. Приведя доказательство Ньютона, Беркли пишет: «Однако очевидно, что для получения момента или приращения прямоугольника АВ прямым и истинным методом необходимо взять стороны такими, какими они получились в результате увеличения их на полные приращения, и затем перемножить их (А + а) x (В + b), а полученное произведение (АВ + аВ + bА + ab) и есть увеличенный прямоугольник. Отсюда, если мы вычтем АВ, остаток (aВ + bА + ab) и будет истинным приращением прямоугольника, превышающим тот, который был получен предыдущим незаконным и непрямым методом, на величину ab. И это справедливо в любом случае, какими бы ни были величины а и b — большими или малыми, конечными или бесконечно малыми, приращениями, моментами или скоростями». Говоря о методе вычисления флюксий с помощью исчезающих величин, он пишет: «Правда, надо признать, что он использовал флюксии подобно лесам при строительстве здания, которые нужно было отбросить в сторону или от которых нужно было избавиться, когда уже было найдено, что конечные линии пропорциональны этим флюксиям. Но ведь эти конечные показатели определяются с помощью флюксий. Поэтому все, что получается с помощью таких показателей и пропорций, необходимо отнести за счет флюксий, которые, следовательно, предварительно надо понять. А что такое эти флюксии? Скорости исчезающих приращений. А что такое эти самые исчезающие приращения? Они не есть ни конечные величины, ни величины бесконечно малые, но они и не нули. Разве мы не имеем права назвать их призраками исчезнувших величин?»Эйлер и анализ бесконечно малых
Если Ньютон и Лейбниц считаются создателями дифференциального и интегрального исчисления, то Эйлера можно назвать создателем математического анализа — области математики, куда входят оба эти раздела. В этом смысле его книги «Введение в анализ бесконечно малых» (1748), «Наставление по дифференциальному исчислению» (1755) и «Интегральное исчисление» (1768—1770) сыграли ключевую роль в оформлении структуры этой новой дисциплины. Трактат «Введение в анализ бесконечно малых» стал для математического анализа тем же, что «Начала» Евклида для геометрии. В этом трактате Эйлер указывает, что функция является основным предметом изучения в анализе, систематизирует работы предшественников об элементарных функциях, изучает их, не прибегая к дифференциальному или интегральному исчислению, однако обильно использует бесконечно большие и бесконечно малые величины (см. приложение). Он также всеми возможными способами старается избежать геометрических рассуждений и чертежей, отдавая предпочтение аналитике и формулам. Структуру дифференциального исчисления он изложил во второй книге трилогии. Хотя Эйлер был последователем Лейбница, в «Наставлении по дифференциальному исчислению» он понимает дифференциал как разницу, однако вносит изменения в исчисление Лейбница. С учетом поправок Эйлера понятие дифференциала приближается к понятию ньютоновской «исчезающей величины». Извечные сомнения, касающиеся бесконечно малых, Эйлер развеял так. По его мнению, важнее было не то, что такое бесконечно малые величины, а то, как они себя ведут. В этом смысле для Эйлера бесконечно малые были равны нулю или в итоге приравнивались к нулю; важнее то, что эти величины могут делиться друг на друга. Результат подобного деления, по сути эквивалентного 0/0, может равняться четко определенному конечному числу. Так, дифференциалы dx, dy играют главную роль при определении значения дроби dy/dx.. Исчисление описывает, как вычислить эту дробь, когда приращения «исчезают». В «Наставлении по дифференциальному исчислению» Эйлер описывает «метод определения пропорции исчезающих приращений, которые получают функции, когда аргументы функции получают одно из таких приращений». Иными словами, в анализе Эйлера вводится отношение приращений определяющее производную функции — понятие, которое заменило дифференциалы dx, dy, занимающие почетное место в исчислении Лейбница. Внесенные Эйлером изменения приблизили понятия дифференциального исчисления Лейбница к понятию предела, которое впоследствии использовал Коши.
В последнем труде трилогии Эйлера, «Интегральное исчисление», интегрирование описывается как операция, обратная дифференцированию. Интегрирование по-прежнему соответствовало понятию площади, но потеряло независимый характер, который отстаивал Лейбниц, что помогло Коши при введении понятия определенного интеграла.
определяющее производную функции — понятие, которое заменило дифференциалы dx, dy, занимающие почетное место в исчислении Лейбница. Внесенные Эйлером изменения приблизили понятия дифференциального исчисления Лейбница к понятию предела, которое впоследствии использовал Коши.
В последнем труде трилогии Эйлера, «Интегральное исчисление», интегрирование описывается как операция, обратная дифференцированию. Интегрирование по-прежнему соответствовало понятию площади, но потеряло независимый характер, который отстаивал Лейбниц, что помогло Коши при введении понятия определенного интеграла.
ЭЙЛЕР ВЕЛИКИЙ
Эйлер был одним из величайших математиков всех времен и, вне всяких сомнений, лучшим математиком XVIII века. Он родился в 1707 году в Базеле, окончил местный университет, брал частные уроки у Иоганна Бернулли, одного из учеников Лейбница. В 1727 году он переехал в Санкт-Петербург, был членом Петербургской академии наук с 1731 по 1741 год, затем переехал в Пруссию и был избран членом Берлинской академии наук. Несмотря на непростые отношения с прусским королем Фридрихом II, он прожил в Берлине 25 лет, после чего вернулся в Санкт-Петербург, где умер в 1783 году.

Портрет Леонарда Эйлера кисти Иоганна Георга Брюкнера.
Д’Аламбер, Лагранж и Карл Маркс
Шел XVIII век, и Д’Аламбер, который обладал намного большим авторитетом в математике, чем Беркли, критически отнесся к понятию бесконечно малых: «Величина есть нечто или ничто; если она — нечто, то она еще не исчезла, если она ничто, то она исчезла в буквальном смысле. Предположение о том, что существует промежуточное состояние между этими двумя, есть химера». Д’Аламбер во французской Энциклопедии дает примитивное определение предела, на которое Коши опирался при разработке фундамента математического анализа: «Одна величина называется пределом второй, если вторая может приблизиться к первой настолько, что будет отличаться от нее менее, чем на любую данную величину, но никогда не будет совпадать с ней». В своей статье о дифференциалах для этой же энциклопедии Д’Аламбер указал путь к четкому определению исчисления: «Ньютон использовал другой принцип, и можно сказать, что метафизика этого великого математика об исчислении флюксий очень точна и ясна, несмотря на то что допускает несовершенное толкование его мыслей. Я никогда не рассматривал дифференциальное исчисление как изучение бесконечно малых величин, но как метод первых и последних рассуждений, или, что есть одно и то же, метод нахождения пределов рассуждениям. Кто-то может счесть, что допущение бесконечно малых величин необходимо лишь для сокращения и упрощения рассуждений, но дифференциальное исчисление необязательно предполагает существование подобных величин. Более того, это исчисление заключается лишь в алгебраическом определении пределов рассуждения».
Мраморная статуя французского философа и математика Д’Аламбера.

Карл Маркс проявлял большой интерес к построению фундамента математического анализа.
Совершенно иным путем следовал Лагранж, который в своей книге «Теория аналитических функций», опубликованной в 1797 году, определил производную f’(x) функции f(х) в точке x как коэффициент при h в разложении в степенной ряд функции f(x + h). Именно Лагранж ввел термин «производная» и первым стал обозначать производную функции f знаком апострофа — f’. К сожалению, его усилия оказались безуспешными и завершились неудачей, поскольку, как позднее показал Коши, функция f необязательно совпадает со степенным рядом, полученным на ее основе. Стоит отметить, что работы Лагранжа по построению фундамента математического анализа очень ценил философ Карл Маркс, основатель марксизма. Маркс даже написал несколько трудов о производных и интегралах (1863—1883), однако в этот период уже появились работы Вейерштрасса, в которых была сформирована прочная основа математического анализа. Маркс рассматривал три этапа развития исчисления: мистическое дифференциальное исчисление Лейбница и Ньютона, рациональное дифференциальное исчисление Д’Аламбера и чисто алгебраическое исчисление Лагранжа. О математиках первого этапа он писал: «Они сами определили загадочный характер недавно открытого исчисления, что привело к получению верных результатов с помощью определенно ошибочных математических преобразований». К Д’Аламберу и Лагранжу он относился более снисходительно: «Д’Аламбер, лишив дифференциальное исчисление мистической завесы, совершил огромный шаг вперед. <…> Лагранж взял за основу теорему Тейлора, которая является наиболее общей и широкой, и в то же время описывает рабочую формулу дифференциального исчисления».Огюстен Коши
В первой половине XIX века был окончательно сформирован четкий фундамент анализа бесконечно малых. Решение этой задачи начал Коши, а завершил Вейерштрасс. Значимый вклад также внес Бернард Больцано своими работами о непрерывных функциях, которые выходят за рамки этой книги. Коши удалось создать математическое течение, целью которого было добиться большей строгости доказательств. Это течение стало основополагающим для математики XIX века. Эту точку зрения он пытался донести до своих учеников в Политехнической школе, где преподавал с 1817 по 1830 год, а также излагал в своих работах. Основными его трудами, о которых мы упомянем, были «Курс анализа» (1821) и «Резюме лекций по исчислению бесконечно малых» (1823). «Курс анализа» был ответом Коши на критику со стороны его коллег по ученому совету Политехнической школы, высказанную в адрес его методики преподавания механики и анализа студентам первого года обучения. Во введении он явно указывает цель своей работы: «Я попытался изложить методы, требуемые геометрией, никогда не обращаясь к аргументам, следующим из общности алгебры. Рассуждения такого типа, которые иногда допускаются, особенно при переходе от сходящихся рядов к расходящимся и от вещественных величин к мнимым, лишь указывают путь к истине и не связаны с точностью, которой должна гордиться математика». «Общность алгебры», о которой упоминает Коши, означает признанный всеми с конца XVI века факт, согласно которому все, что верно для вещественных чисел, так же верно и для комплексных; все, что верно для конечных величин, применимо и к бесконечным; все, что верно для сходящихся рядов, верно и для расходящихся. В качестве основного понятия анализа бесконечно малых Коши предложил понятие предела, которое определил так: «Когда последовательные значения переменной бесконечно приближаются к конкретному значению так, что в итоге отличаются от него на произвольно выбранную величину, последнее значение называется пределом остальных». Используя понятие предела, Коши определил бесконечно малые как переменные, которые стремятся к нулю: «Когда последовательные значения переменной бесконечно уменьшаются так, что становятся меньше любой заданной величины, эта переменная называется бесконечно малой. Предел таких переменных равен нулю». Он также ввел понятие предела последовательности, которое с дополнениями Вейерштрасса используется и сейчас. Коши также установил, что можно говорить о сумме ряда лишь в том случае, когда он сходится, и определил ее как предел последовательности частичных сумм ряда. На пятистах страницах «Курса анализа» также приводятся определения непрерывной функции, комплексного числа, формулируются критерии сходимости рядов и так далее. Работы Коши о сходимости рядов вызвали большое возбуждение. Рассказывают, что после собрания Французской академии наук, где ученый изложил свои идеи о сходимости рядов, обеспокоенный Лаплас заперся у себя дома и не выходил, пока не проверил, что все ряды, использованные им в «Небесной механике», сходятся, и лишь тогда вздохнул с облегчением. Коши планировал, что «Курс анализа» будет состоять из двух томов, но неблагоприятные отзывы заставили его отказаться от написания второго тома. Суть критики сводилась к тому, что книга, по мнению руководства Политехнической школы, не подходила для образования будущих инженеров. Поэтому Коши решил пересмотреть идею о публикации второго тома и вместо этого выпустил дополнение к «Курсу анализа», представлявшее собой краткое изложение его лекций. Первый том увидел свет в 1823 году под названием «Резюме лекций по исчислению бесконечно малых», где давалось современное определение производной как предела когда h стремится к 0.
когда h стремится к 0.
КОШИ: СТРОГОСТЬ ПРЕВЫШЕ ВСЕГО
Огюстен Луи Коши родился в 1789 году, спустя несколько месяцев после начала Великой французской революции. Он занимает почетное место среди ведущих математиков первой половины XIX века. Благодаря ему был сделан значимый шаг в сторону большей логической строгости математических рассуждений. Так, в статье Энциклопедии Британника о нем сказано: «Коши был одним из величайших математиков современности. Одним из наиболее значительных его достижений является четкость и строгость введенных им методов. Первый этап логической строгости, характерной для современной математики, берет начало в его лекциях и книгах по математическому анализу, написанных в 1820-1830 годах». Также всегда указывается, что он был разносторонне образованным человеком и интересовался классическими языками. Он был ревностным католиком и яростно защищал право Бурбонов на французский престол, дарованное Богом. «Его коллеги часто упрекали его в непреклонном ханжестве и агрессивном религиозном фанатизме»,- говорится об этом в уже упомянутой Энциклопедии Британника. Он был преподавателем Политехнической школы и членом Французской академии наук. По политическим мотивам ему пришлось покинуть Францию на период с 1830 по 1838 год. Умер Коши в 1857 году.

Французская марка, выпущенная в честь 200-летия со дня рождения Коши.
В «Резюме лекций по исчислению бесконечно малых» также приводится определение интеграла непрерывной функции
 как предела сумм Коши:
как предела сумм Коши:
 где a < х1 < х2 < … < xn-1 < b — разбиение интервала [а, b], а искомый интеграл рассчитывается как предел при разбиении интервала на отрезки, длины которых стремятся к 0.
где a < х1 < х2 < … < xn-1 < b — разбиение интервала [а, b], а искомый интеграл рассчитывается как предел при разбиении интервала на отрезки, длины которых стремятся к 0.
 ряд Тейлора для которой в точке 0 сходится, но отличается от функции в окрестности нуля. Это доказывает невозможность выстраивания анализа бесконечно малых поверх прочной основы, предложенной Лагранжем.
Мы не будем говорить о других работах Коши и резюме его лекций, а расскажем о значимости его трудов в формировании основы анализа бесконечно малых.
Несомненно, его попытки логически обосновать анализ бесконечно малых были значимым этапом, но тем не менее не окончательным. Нильс Абель, великий норвежский математик, одним из первых обратил внимание на важность работ Коши, отметив их строгость и вместе с тем неполноту. Одновременно с этим он указал, в чем именно заключаются недостатки работ Коши. Это был очередной шаг вперед на пути, который полностью был пройден в середине XIX века с появлением работ Вейерштрасса. Окончательное и четкое определение вещественных чисел было дано еще два десятилетия спустя. Сам Абель в статье, опубликованной в 1826 году, доказал, что одна из теорем «Курса анализа» Коши «допускала исключения» (оцените дипломатичность формулировки!). Эта теорема Коши была не единственной, «допускающей исключения».
ряд Тейлора для которой в точке 0 сходится, но отличается от функции в окрестности нуля. Это доказывает невозможность выстраивания анализа бесконечно малых поверх прочной основы, предложенной Лагранжем.
Мы не будем говорить о других работах Коши и резюме его лекций, а расскажем о значимости его трудов в формировании основы анализа бесконечно малых.
Несомненно, его попытки логически обосновать анализ бесконечно малых были значимым этапом, но тем не менее не окончательным. Нильс Абель, великий норвежский математик, одним из первых обратил внимание на важность работ Коши, отметив их строгость и вместе с тем неполноту. Одновременно с этим он указал, в чем именно заключаются недостатки работ Коши. Это был очередной шаг вперед на пути, который полностью был пройден в середине XIX века с появлением работ Вейерштрасса. Окончательное и четкое определение вещественных чисел было дано еще два десятилетия спустя. Сам Абель в статье, опубликованной в 1826 году, доказал, что одна из теорем «Курса анализа» Коши «допускала исключения» (оцените дипломатичность формулировки!). Эта теорема Коши была не единственной, «допускающей исключения».
УПРЯМ, НО ТОЧЕН
Нильс Хенрик Абель (1802-1829) был одним из наиболее ожесточенных противников отсутствия математической строгости: «В высшей математике, — писал он в 1826 году, — лишь некоторые предположения доказаны с неоспоримой строгостью. Неизменно встречается печальная привычка выводить общее из частного, и, несомненно, весьма заметно, что результатами подобных рассуждений чаще всего являются парадоксы». Поэтому неудивительно, что Абель изучал тексты Коши и ценил его стремление внести строгость и порядок в математику. «Коши упрям,- писал Абель, будучи в Париже в 1826 году,- и с ним нельзя договориться, но именно он сегодня лучше всех знает, как следует обращаться с математикой. Его работы удивительны, но достаточно запутаны. Сперва я ничего в них не понял, но теперь начинаю понимать их более ясно». В статье о биноме Ньютона, опубликованной в 1826 году, он пишет: «Курс анализа» Коши следует прочитать всякому аналитику, который хочет действовать в своих математических исследованиях со всей строгостью».

Банкнота в 500 норвежских крон, на которой изображен Абель.
Однако усилия Коши по приданию математическому анализу большей строгости были лишь очередным промежуточным этапом развития этой дисциплины. Доказательством этому служит то, что исследователи работ ученого не пришли к единому выводу об истинности или ошибочности его теорем. Это кажущееся противоречие вызвано тем, что определения, представленные Коши в «Курсе анализа», были неточными и нечеткими и порой допускали несколько толкований. Неоднозначность этих определений лучше всего объясняет Айвор Граттангиннес: «Достаточно сказать, что использованные им технические термины заслуживают внимания, и в теореме Коши, как и во всем его анализе, они применяются крайне свободно».Эйлер, Коши и эстетическая ценность математики
Следует рассказать и об эстетическом начале, поскольку, вопреки мнению многих, эстетика не только не чужда математике, но и составляет ее значимую часть. Название этой главы — «Укрощенные бесконечно малые» — указывает, что Коши совершил решающий шаг, преодолев с помощью теории пределов логические проблемы, возникавшие в анализе бесконечно малых с XVII века. Как мы уже говорили выше, бесконечно большим и бесконечно малым величинам изначально не было дано логически строгого и четкого определения. В этом смысле, например, «Введение в анализ бесконечно малых» Эйлера является недостаточно логичным. По этой причине математики в итоге стали отдавать предпочтение пределам. Однако теперь нам известно, что рассуждения Эйлера с использованием бесконечно малых столь же строги, как и современные рассуждения, в которых используются пределы. Строго говоря, логический фундамент анализа XVIII века сформировал Абрахам Робинсон в 1966 году. На основе теории моделей он показал, что вещественные числа можно расширить множеством бесконечно малых, с которыми можно производить стандартные арифметические операции. Созданный им раздел математики получил название «нестандартный анализ». Теперь, как и было обещано, мы расскажем об эстетической составляющей математики, так как рассуждения Эйлера во «Введении в анализ бесконечно малых» намного красивее, чем рассуждения, записанные с использованием пределов. Математику часто называют сухой наукой, которая изучает идеальные абстрактные объекты, числа и треугольники, наукой, в которой нет места эмоциям. Это совершенно не так. Профессиональные математики выбрали свою профессию по разным причинам, но всех их объединяет одно: математика представляет для них источник сильных эмоций. Эрнест Уильям Хобсон (1856—1933) сказал о «Введении в анализ бесконечно малых»: «Будет непросто найти другой труд в истории математики, который оставляет у читателя такое впечатление о гениальности его автора, как этот». Любой, кто читал его, полностью согласится с Хобсоном. Это впечатление создается потому, что труд Эйлера вызывает бурные эмоции, оставляет след. Гениальность Эйлера нашла воплощение в красоте его работы, в ее эстетической ценности, выходящей далеко за рамки простой математики. Иными словами, эта книга не только обладает свойствами, о которых говорит Харолд Харди (1877—1947) в своей знаменитой «Апологии математика», рассуждая о красоте математических идей. В ней также присутствуют общие эстетические категории, о которых писали Иммануил Кант, Теодор Адорно и Джордж Сантаяна. Один из самых удивительных результатов, содержащихся в труде Эйлера, как с математической, так и с эстетической точки зрения — это разложение функции синуса в бесконечный ряд: а также то, как Эйлер использует этот ряд вместе с разложением в степенной ряд для нахождения суммы следующих бесконечных степенных рядов:
а также то, как Эйлер использует этот ряд вместе с разложением в степенной ряд для нахождения суммы следующих бесконечных степенных рядов:
 Живительно, что эти потрясающе красивые результаты, которые не смогли найти Лейбниц, братья Бернулли и, возможно, сам Ньютон, Эйлер смог вывести с помощью бесконечно малых всего на нескольких строках. Его рассуждения просты и гениальны, и можно четко проследить, какие идеи позволили ему совершить эти открытия. Если попытаться переписать эти рассуждения, используя теорию пределов, они теряют значительную долю простоты и красоты. Чтобы убедиться в этом, достаточно сравнить выкладки Эйлера во «Введении в анализ бесконечно малых» и последние страницы «Курса анализа» Коши (примечания VIII и IX). Коши пытается подтвердить правильность результатов Эйлера с помощью пределов, в результате чего элегантные и краткие рассуждения Эйлера, занимающие несколько строк, превращаются в несколько десятков страниц вычислений. Можно без преувеличения сказать, что Коши превратил деликатный эротизм Эйлера в порнографию.
Живительно, что эти потрясающе красивые результаты, которые не смогли найти Лейбниц, братья Бернулли и, возможно, сам Ньютон, Эйлер смог вывести с помощью бесконечно малых всего на нескольких строках. Его рассуждения просты и гениальны, и можно четко проследить, какие идеи позволили ему совершить эти открытия. Если попытаться переписать эти рассуждения, используя теорию пределов, они теряют значительную долю простоты и красоты. Чтобы убедиться в этом, достаточно сравнить выкладки Эйлера во «Введении в анализ бесконечно малых» и последние страницы «Курса анализа» Коши (примечания VIII и IX). Коши пытается подтвердить правильность результатов Эйлера с помощью пределов, в результате чего элегантные и краткие рассуждения Эйлера, занимающие несколько строк, превращаются в несколько десятков страниц вычислений. Можно без преувеличения сказать, что Коши превратил деликатный эротизм Эйлера в порнографию.
Карл Вейерштрасс
В первой половине XIX века математики начали задумываться над тем, что постулаты евклидовой геометрии не являются априори истинными и что отрицание этих постулатов, в особенности постулата о параллельности прямых, может привести к созданию принципиально новой геометрии, столь же корректной, как и геометрия Евклида. Это было продемонстрировано в работах Николая Ивановича Лобачевского (1792—1856) и Яноша Бойяи (1802—1860). Этого же мнения придерживался великий Гаусс, однако он действовал излишне осмотрительно и поделился своими идеями лишь с немногими соратниками, из-за чего принятие неевклидовой геометрии в научных кругах происходило не так быстро, как могло бы. Процесс создания неевклидовой геометрии завершил Бернхард Риман (1826—1866). Риман в своем докладе «О гипотезах, лежащих в основании геометрии», который он сделал 10 июня 1854 года с целью получить пост преподавателя в Гёттингенском университете, представил общую теорию геометрии, простиравшуюся намного дальше, чем частные случаи, описанные Лобачевским и Бойяи, которые были получены отрицанием постулата о параллельности прямых. Риман сделал основой своей геометрии утверждение, над которым другие математики размышляли в течение 50 лет: постулат о параллельности, равно как и любой другой постулат евклидовой геометрии, не является априори истинным в абсолютном пространстве, а, напротив, представляет собой эмпирический результат, полученный в процессе наблюдения той небольшой части пространства, что нас окружает. Спустя некоторое время после смерти Гаусса была опубликована его частная переписка, где он восхвалял новую геометрию предшественников Римана — Лобачевского и Бойяи. Если бы кто-то узнал о том, какой интерес и энтузиазм проявлял великий Гаусс по отношению к неевклидовой геометрии, это стало бы решающим толчком к ее широкому принятию. Как следствие, это серьезно повлияло бы на вопросы, связанные с математической и логической строгостью. Корректность этих результатов, не проверенных эмпирическим путем, а доказанных строгими геометрическими рассуждениями, оставалась под сомнением. Таким образом, геометрия Евклида перестала быть неэмпирической дисциплиной, на основе которой с математической строгостью строились другие разделы математики. Ее место быстро заняла арифметика — раздел математики, изучающий числа и их свойства.
Карл Вейерштрасс считается создателем современного анализа. Здесь он изображен на портрете кисти немецкого художника Конрада Фера.
В этом смысле Карл Вейерштрасс (1815—1897) пересмотрел определение предела Коши и убрал из него геометрические элементы, в частности формулировки «бесконечно приближаются», «бесконечно уменьшаются» и «меньше любой заданной величины», заменив их арифметическими выражениями, в которых фигурировали величины эпсилон и дельта, используемые и сейчас: «Предел функции f(х) равен 1, когда x стремится к а, если для любого положительного ε > 0 существует другое положительное число δ > 0 такое, что для любой точки x, в которой определена данная функция, выполняется неравенство 0 < |f(x) — 1| < ε. С конца 1850-х до конца 1880-х годов Вейерштрасс преподавал в Берлинском университете. Он не публиковал свои лекции, и данные им определения дошли до нас из конспектов его учеников. Начиная со второй половины XIX века Германия постепенно становилась мировым математическим центром, придя на смену Франции, что способствовало эффективному распространению анализа Вейерштрасса.Заключение
Начиная с Эйлера и в особенности после того, как усилиями Коши и Вейерштрасса был выстроен фундамент анализа бесконечно малых, эта дисциплина стала ядром математического анализа. Функции, пределы, производные и интегралы — фундаментальные инструменты математического анализа. С их помощью великое множество физических, технических, экономических и даже медицинских задач можно свести к уравнениям, где будут одновременно использоваться функции, их производные и интегралы. Так, задачи поиска оптимальной формы крыла самолета, определения кровяного давления в венах и артериях организма или выявления роста раковых опухолей решаются с помощью уравнений такого типа. Эти уравнения формулируются с использованием понятий математического анализа, в том числе анализа функций нескольких переменных, а также законов физики. Однако составить такие уравнения — это одно, а уметь решать их — совсем другое. Решения некоторых подобных уравнений были однозначно определены, уже когда Ньютон и Лейбниц создали анализ бесконечно малых, однако большинство из них настолько сложны, что и сегодня не существует способов их точного решения. Математический анализ также описывает методы приближенного и численного решения подобных уравнений, позволяющие найти их корни с определенной точностью. С появлением современных компьютеров в середине XX века в этой области математического анализа произошла революция. Обычные люди, как правило, удивляются, когда слышат, что математики до сих пор совершают новые открытия. В действительности же их число с каждым годом увеличивается экспоненциально. Когда кто-то говорит, что занимается работами в новой области математики, несведущие задают вопрос: «А разве в ней еще не все известно?» Разумеется, это не так. Нам неизвестно множество уравнений, описывающих загадки природы, решение которых будет способствовать прогрессу человечества. Технологический прогресс и развитие медицинских и экономических методов ставят перед учеными новые задачи, и математикам ежедневно приходится их решать. Эта книга начинается с фразы: «Анализ бесконечно малых, вне всяких сомнений, наиболее мощное и эффективное средство изучения природы, когда-либо созданное математиками». Однако наука ставит перед нами столько задач, что в математическом анализе, пришедшем на смену анализу бесконечно малых, непрерывно требуется разрабатывать новые техники и приемы их решения.Приложение. Эйлер и бесконечно малые
Чтобы показать, как используются бесконечно большие и малые величины, приведем пример разложения функции ez в степенной ряд. Этот пример продемонстрирован Эйлером в книге «Введение в анализ бесконечно малых». Сначала Эйлер определяет число е следующим образом. Показательные функции аz, а > 1, описывают множество кривых, которые имеют общую точку (0, 1). Угол наклона касательной к этим кривым в этой точке зависит, разумеется, от основания степени а и бесконечно возрастает от 0, соответствующего а = 1. Число е определяется как число, для которого тангенс угла наклона касательной ez в точке (0,1) равен 1. Иными словами, касательная к кривой е2 в точке (0, 1) описывается уравнением 1 + z. Так как Эйлер понимал кривые как многоугольники со сторонами, имеющими бесконечно малую длину, это означает, что бесконечно малый отрезок кривой у = ez, находящийся в точке с координатами (0,1), что соответствует е0 = 1, совпадает с прямой у = 1 + z. Для бесконечно малых чисел w получим, что они находятся одновременно на прямой и на кривой, которые совпадают на этом бесконечно малом участке. Таким образом, для бесконечно малого w выполняется равенство ew = 1 + w. Для Эйлера это было не приближенное, а строгое равенство. С учетом этого будем записывать данное число z в виде произведения бесконечно малого числа w на бесконечно большое число N:z = wN. Допустим, что z = 2, и запишем его в следующем виде Таким образом,
Таким образом,
 и N = 2 ∙ 101000000. Однако этого недостаточно: это значение w очень мало, но не является бесконечно малым, равно как и N не является бесконечно большим.
Тем не менее читатель легко представит разницу между очень малым и очень большим и между бесконечно малым и бесконечно большим. С учетом свойств показательной функции можно записать: ez = ewN — (ew)N. Так как w является бесконечно малым, то, учитывая равенства, изложенные в нашей дискуссии о касательных, получим: еz = (1 + w)N. Так как w = z/N, это означает:
и N = 2 ∙ 101000000. Однако этого недостаточно: это значение w очень мало, но не является бесконечно малым, равно как и N не является бесконечно большим.
Тем не менее читатель легко представит разницу между очень малым и очень большим и между бесконечно малым и бесконечно большим. С учетом свойств показательной функции можно записать: ez = ewN — (ew)N. Так как w является бесконечно малым, то, учитывая равенства, изложенные в нашей дискуссии о касательных, получим: еz = (1 + w)N. Так как w = z/N, это означает:
 где N — бесконечно большое число. Запишем это равенство в следующем виде:
где N — бесконечно большое число. Запишем это равенство в следующем виде:
 Применим теорему о биноме:
Применим теорему о биноме:
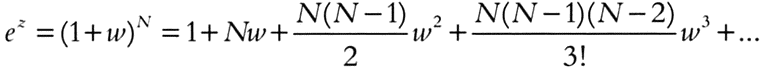 Так как N — бесконечно большое, получим, что N — 1 = N, N — 2 = N и так далее, что позволяет преобразовать равенство:
Так как N — бесконечно большое, получим, что N — 1 = N, N — 2 = N и так далее, что позволяет преобразовать равенство:
 Заметим, что в методе Эйлера для разложения показательной функции в ряд бесконечно большие и бесконечно малые числа появляются и исчезают, подобно предметам в руках у фокусника. Тем не менее они используются не напрасно: они помогают преобразовать функцию и выявить ее важные скрытые свойства.
Этот метод Эйлера по разложению в ряд кажется недостаточно строгим, но здесь не идет речь о логической строгости рассуждений Эйлера. К тому же следует отметить, что на самом деле они всего лишь подразумевают использование более сложной логики, чем та, что лежит в основе стандартного анализа.
В некотором смысле эти выкладки Эйлера демонстрируют его гениальность. Как мы уже говорили в главе 6, Хобсон так отзывался о «Введении в анализ бесконечно малых»: «Будет непросто найти другой труд в истории математики, который оставляет у читателя такое впечатление о гениальности его автора, как этот».
Заметим, что в методе Эйлера для разложения показательной функции в ряд бесконечно большие и бесконечно малые числа появляются и исчезают, подобно предметам в руках у фокусника. Тем не менее они используются не напрасно: они помогают преобразовать функцию и выявить ее важные скрытые свойства.
Этот метод Эйлера по разложению в ряд кажется недостаточно строгим, но здесь не идет речь о логической строгости рассуждений Эйлера. К тому же следует отметить, что на самом деле они всего лишь подразумевают использование более сложной логики, чем та, что лежит в основе стандартного анализа.
В некотором смысле эти выкладки Эйлера демонстрируют его гениальность. Как мы уже говорили в главе 6, Хобсон так отзывался о «Введении в анализ бесконечно малых»: «Будет непросто найти другой труд в истории математики, который оставляет у читателя такое впечатление о гениальности его автора, как этот».
Библиография
AlTON, E.J., Leibniz. Una biografia, Madrid, Alianza Editorial, 1992. BARON, M.E., The Origins of the Infinitesimal Calculus, Oxford, Pergamon, 1969. DURAN, A.J., Historia, con personajes, de los conceptos del cdlculo, Madrid, Alianza Editorial, 1996. DURAN, A.J., (coordinador), El legado de las matemdticas, Sevilla, Real Sociedad Matematica Espanola у otros, 2000. DURAN, A.J., La polemica sobre la invencion del cdlculo infinitesimal, Barcelona, Critica, 2006. DURAN, A.J., Pasiones, piojos, dioses… у matemdticas, Barcelona, Destino, 2009. DURAN, A.J., Cauchy, hijo rebelde de la revolution, Madrid, Nivola, 2009. EULER, L., Introductio in analysin infinitorum, edicion facsimilar у critica con traduction al castellano de J.L. Arantegui у notas de Antonio J. Duran, Sevilla, Real Sociedad Matematica Espanola у SAEM Thales, 2000. EDWARDS, C.H,, The Historical Development of the Calculus, Nueva ^fork, Springer-Verlag, 1979. HALL, A.R., Philosophers at War, Cambridge, Cambridge University Press, 1980. HOFMANN, J.E., Leibniz in Paris, 1672-1676. His Growth to Mathematical Maturity, Cambridge, Cambridge University Press, 1974. MANUEL, F.E., A Portrait of Isaac Newton, Harvard University Press, Cambridge (Mass.), 1968. NEWTON, L, The Mathematical Papers of Isaac Newton, edicion de D.T. Whiteside, Cambridge, Cambridge University Press, 1967-1981. NEWTON, I., Analysis per quantitatum series, fluxiones, ac differentias, edicion facsimilar у critica con traduccion al castellano de J.L. Arantegui у notas de Antonio J. Duran, Sevilla, Real Sociedad Matematica Espanola у SAEM Thales, 2003. WESTFALL, R.S., Never at Rest; a Biography of Isaac Newton, Cambridge, Cambridge University Press, 1983.
Последние комментарии
18 часов 38 минут назад
1 день 10 часов назад
1 день 19 часов назад
1 день 19 часов назад
4 дней 1 час назад
4 дней 6 часов назад